Convergence in distribution describes the behavior of a sequence of random variables whose cumulative distribution functions approach a limiting distribution as the sample size grows. This concept is fundamental in probability theory and statistics for understanding the asymptotic properties of estimators and test statistics. Explore the rest of the article to grasp how convergence in distribution impacts your statistical analyses and inference.
Table of Comparison
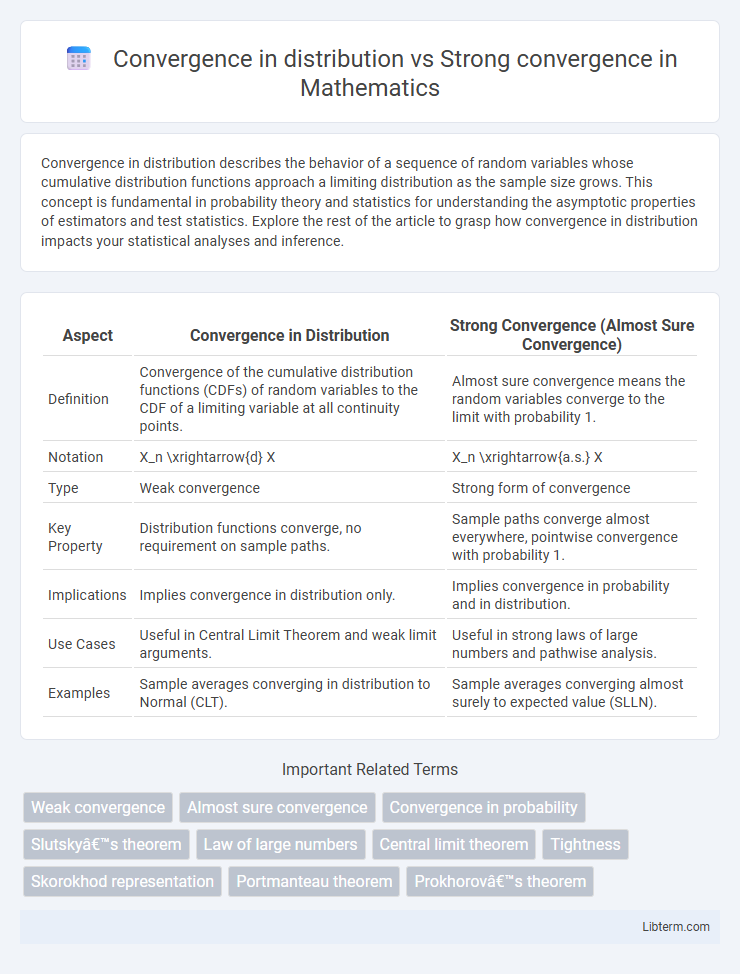
| Aspect | Convergence in Distribution | Strong Convergence (Almost Sure Convergence) |
|---|---|---|
| Definition | Convergence of the cumulative distribution functions (CDFs) of random variables to the CDF of a limiting variable at all continuity points. | Almost sure convergence means the random variables converge to the limit with probability 1. |
| Notation | X_n \xrightarrow{d} X | X_n \xrightarrow{a.s.} X |
| Type | Weak convergence | Strong form of convergence |
| Key Property | Distribution functions converge, no requirement on sample paths. | Sample paths converge almost everywhere, pointwise convergence with probability 1. |
| Implications | Implies convergence in distribution only. | Implies convergence in probability and in distribution. |
| Use Cases | Useful in Central Limit Theorem and weak limit arguments. | Useful in strong laws of large numbers and pathwise analysis. |
| Examples | Sample averages converging in distribution to Normal (CLT). | Sample averages converging almost surely to expected value (SLLN). |
Introduction to Modes of Convergence in Probability
Convergence in distribution describes the scenario where the cumulative distribution functions of random variables approach the cumulative distribution function of a limiting random variable at all continuity points. Strong convergence, also known as almost sure convergence, requires that random variables converge to a limit with probability one, implying a more stringent form of convergence than convergence in distribution. These modes of convergence are fundamental in probability theory, with convergence in distribution often used in limit theorems, while strong convergence guarantees pointwise limits almost everywhere.
Defining Convergence in Distribution
Convergence in distribution, also known as weak convergence, occurs when the cumulative distribution functions (CDFs) of a sequence of random variables converge pointwise to the CDF of a limiting random variable at all continuity points. This form of convergence characterizes the convergence of distributions rather than individual outcomes, making it weaker than strong (almost sure) convergence, which requires the random variables themselves to converge almost surely to a limit. Defining convergence in distribution emphasizes the convergence of probability measures and is fundamental in proving the central limit theorem and other limit laws in probability theory.
Exploring Strong Convergence (Almost Sure Convergence)
Strong convergence, also known as almost sure convergence, occurs when a sequence of random variables converges to a limit with probability one, meaning the values stabilize pointwise except on a set of probability zero. This type of convergence provides a stronger guarantee than convergence in distribution, which only requires the cumulative distribution functions to converge at continuity points. Strong convergence ensures that for almost every outcome, the sequence values approach the limiting random variable, making it crucial in stochastic process analysis and pathwise estimation.
Mathematical Formalisms: Distribution vs Strong Convergence
Convergence in distribution, also known as weak convergence, is defined by the convergence of the cumulative distribution functions of random variables to the cumulative distribution function of a limiting variable at all continuity points. Strong convergence, or almost sure convergence, requires that the sequence of random variables converges to the limiting variable with probability one, meaning \( P(\lim_{n \to \infty} X_n = X) = 1 \). While convergence in distribution concerns the behavior of probability measures and is weaker, strong convergence involves pointwise convergence almost everywhere, making it a stronger and more informative form of probabilistic limit.
Key Differences Between the Two Convergences
Convergence in distribution describes the scenario where the cumulative distribution functions of random variables approach the distribution function of a limiting variable, emphasizing the alignment of distribution shapes rather than exact sample outcomes. Strong convergence, or almost sure convergence, requires the random variables to converge pointwise to the limiting variable with probability one, ensuring individual sample paths closely match in the limit. The primary difference lies in the strength of convergence: convergence in distribution focuses on the behavior of the distributions overall, whereas strong convergence guarantees convergence of the actual sequences of random variables almost everywhere.
Examples Illustrating Convergence in Distribution
Convergence in distribution occurs when the cumulative distribution functions of random variables approach the cumulative distribution function of a limiting variable, exemplified by the Central Limit Theorem where normalized sums of independent identically distributed variables converge to a normal distribution. Strong convergence, or almost sure convergence, requires that the sequence of random variables converges to the limiting variable with probability one, evident in the Law of Large Numbers where sample averages almost surely converge to the expected value. Examples of convergence in distribution include the binomial distribution approaching the Poisson distribution under specific parameter limits and the convergence of scaled geometric random variables to the exponential distribution.
Examples of Strong (Almost Sure) Convergence
Strong convergence, also known as almost sure convergence, occurs when a sequence of random variables converges to a limit with probability one, exemplified by the Strong Law of Large Numbers where the sample average converges almost surely to the expected value. In contrast, convergence in distribution focuses on the distribution functions converging to a limit distribution, without requiring pointwise convergence of random variables. A classic example of strong convergence is the empirical distribution function converging almost surely to the true distribution function as the sample size increases.
Implications in Statistical Inference and Probability Theory
Convergence in distribution ensures that the cumulative distribution functions of random variables approach a limit, supporting the validity of asymptotic approximations in hypothesis testing and confidence interval construction. Strong convergence, or almost sure convergence, implies the random variables themselves converge pointwise with probability one, providing stronger guarantees for consistency and stability of estimators in statistical inference. In probability theory, these distinctions affect limit theorems' applications: convergence in distribution underlies central limit theorem results, while strong convergence is crucial for almost sure laws such as the law of large numbers.
Practical Applications and Relevance in Data Science
Convergence in distribution is crucial for understanding the asymptotic behavior of estimators and hypothesis testing in data science, as it guarantees that the sampling distribution stabilizes to a target distribution, enabling reliable inference from large datasets. Strong convergence, also known as almost sure convergence, ensures that sequences of random variables converge pointwise with probability one, which is vital for algorithmic consistency and the stability of iterative machine learning methods. Practical applications in data science involve using convergence in distribution for confidence interval construction and p-value calculation, while strong convergence supports the reliability of stochastic optimization algorithms and guarantees in reinforcement learning.
Summary: Choosing the Appropriate Convergence Concept
Convergence in distribution focuses on the behavior of the cumulative distribution functions of random variables, making it ideal for asymptotic distribution analysis and inference, especially when dealing with non-identically distributed or dependent sequences. Strong convergence, or almost sure convergence, requires random variables to converge pointwise with probability one, providing the strongest form of convergence useful in pathwise consistency and stochastic process applications. Selecting the appropriate convergence depends on the context: use convergence in distribution for limit theorems and weak convergence scenarios, and choose strong convergence when sample path properties and almost sure guarantees are critical.
Convergence in distribution Infographic
 libterm.com
libterm.com