Action-packed scenes drive stories forward by creating excitement and suspense that captivate audiences. Mastering action sequences enhances the emotional impact and keeps viewers engaged from start to finish. Discover how to craft compelling action moments that will elevate your storytelling in the rest of this article.
Table of Comparison
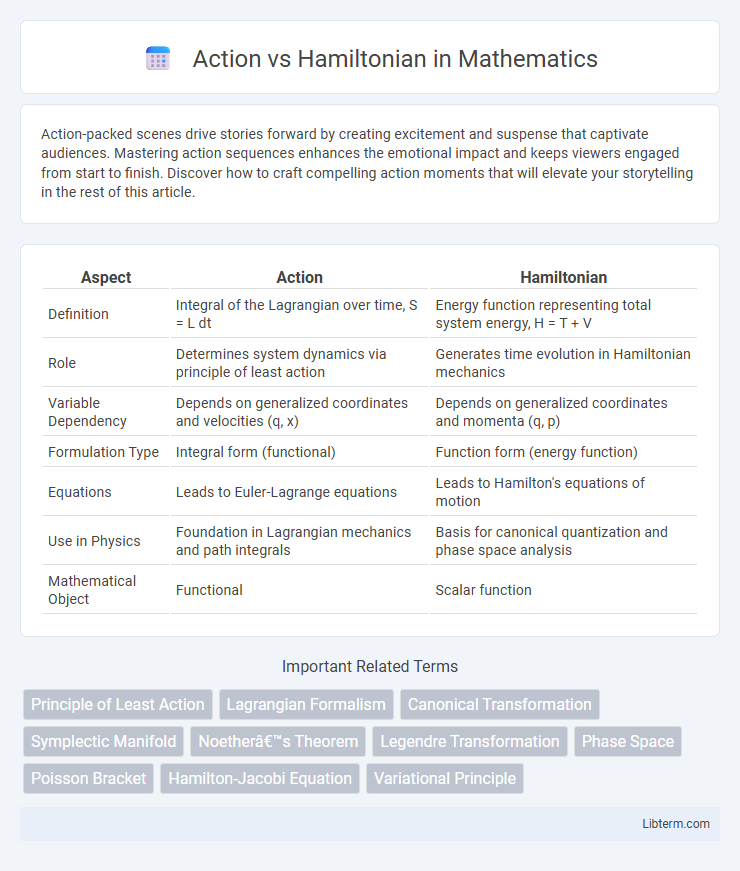
| Aspect | Action | Hamiltonian |
|---|---|---|
| Definition | Integral of the Lagrangian over time, S = L dt | Energy function representing total system energy, H = T + V |
| Role | Determines system dynamics via principle of least action | Generates time evolution in Hamiltonian mechanics |
| Variable Dependency | Depends on generalized coordinates and velocities (q, x) | Depends on generalized coordinates and momenta (q, p) |
| Formulation Type | Integral form (functional) | Function form (energy function) |
| Equations | Leads to Euler-Lagrange equations | Leads to Hamilton's equations of motion |
| Use in Physics | Foundation in Lagrangian mechanics and path integrals | Basis for canonical quantization and phase space analysis |
| Mathematical Object | Functional | Scalar function |
Introduction to Action and Hamiltonian
The action in classical mechanics is a scalar quantity defined as the integral of the Lagrangian over time, encapsulating the dynamics of a system through principles like least action. The Hamiltonian represents the total energy of the system, formulated as a function of generalized coordinates and conjugate momenta, providing a basis for Hamiltonian mechanics and phase space analysis. Understanding the relationship between action and Hamiltonian is fundamental for transition from Lagrangian to Hamiltonian formalisms, facilitating deeper insights into classical and quantum dynamics.
Historical Background of Action and Hamiltonian
The concept of action traces back to Maupertuis and Lagrange in the 18th century, formalized through the principle of least action in classical mechanics, describing the path a system takes to minimize the action integral. Hamiltonian mechanics, developed by William Rowan Hamilton in the 1830s, reformulated classical mechanics using Hamilton's equations, shifting focus from Lagrangian action to energy functions representing total system dynamics. This historical evolution from action to Hamiltonian frameworks laid the foundation for modern analytical mechanics and quantum theory.
Fundamental Concepts: Action Principle
The action principle, a cornerstone of classical mechanics, defines the action as the integral of the Lagrangian over time, encapsulating the dynamics of a system. Hamiltonian mechanics reformulates this principle by expressing the system's total energy in terms of generalized coordinates and momenta, providing a powerful framework for predicting time evolution. The transition from action to Hamiltonian formalism highlights the deep connection between variational principles and the symplectic structure of phase space.
Hamiltonian Mechanics: An Overview
Hamiltonian mechanics offers a reformulation of classical mechanics centered on the Hamiltonian function, which represents the total energy of a system as a function of generalized coordinates and conjugate momenta. Unlike the action principle, which involves finding paths that minimize the action integral, Hamiltonian mechanics uses canonical equations to describe the time evolution of a system through phase space. This approach enables a powerful framework for analyzing complex dynamical systems, facilitating the transition to quantum mechanics and providing deep insights into conservation laws and symplectic geometry.
Mathematical Formulation: Action vs Hamiltonian
The action is a functional defined as the integral of the Lagrangian over time, representing the path taken by a system in configuration space, while the Hamiltonian is a function expressing the total energy, formulated in phase space with coordinates and conjugate momenta. Mathematically, the action \(S\) is given by \(S = \int L(q, \dot{q}, t) \, dt\), and its stationary value leads to the Euler-Lagrange equations. The Hamiltonian \(H(q, p, t)\) is obtained via a Legendre transform of the Lagrangian \(L\) and satisfies Hamilton's equations, which govern the system's evolution in phase space.
Role in Classical Mechanics
The action in classical mechanics is a functional defined as the integral of the Lagrangian over time, serving as the quantity minimized or extremized according to the principle of least action. The Hamiltonian represents the total energy of the system, expressed in terms of generalized coordinates and conjugate momenta, and governs the time evolution of the system via Hamilton's equations. While the action provides a global variational approach to the system's trajectory, the Hamiltonian offers a local, differential formulation of classical dynamics.
Differences in Quantum Mechanics
The action in quantum mechanics describes the integral of the Lagrangian over time, encapsulating a system's dynamic evolution through the principle of least action, while the Hamiltonian represents the total energy operator governing time evolution via Schrodinger's equation. The action provides a path integral formulation approach, allowing summation over all possible trajectories, whereas the Hamiltonian formalism relies on operator algebra in Hilbert space to determine quantum states and observables. Differences highlight that the action emphasizes trajectories in path integrals, and the Hamiltonian focuses on energy eigenstates and time-dependent wavefunctions.
Applications in Physics
The action principle, rooted in Lagrangian mechanics, provides a powerful framework for deriving equations of motion by minimizing the action integral, which is essential in fields like classical mechanics, quantum mechanics, and general relativity. The Hamiltonian formalism facilitates the transition to quantum mechanics by representing the total energy of a system and enabling phase space analysis, crucial for understanding dynamics and conserved quantities. Both approaches complement each other in applications such as quantum field theory, statistical mechanics, and the study of dynamical systems, where they offer distinct yet interconnected tools for solving complex physical problems.
Advantages and Limitations
The action formulation in classical mechanics provides a powerful variational principle that simplifies the derivation of equations of motion and directly connects to path integral quantization in quantum mechanics. The Hamiltonian approach excels in describing energy conservation and symplectic structure, making it ideal for analyzing stability and canonical transformations. However, the action method can be challenging for complex constraints, while the Hamiltonian framework may become cumbersome for systems with non-standard symplectic geometries or time-dependent Hamiltonians.
Conclusion: Comparing Action and Hamiltonian
Action and Hamiltonian represent two fundamental but distinct approaches in classical mechanics. The action, defined as the integral of the Lagrangian over time, provides a global scalar quantity whose stationary value determines the system's trajectory via the principle of least action. In contrast, the Hamiltonian formalism reformulates dynamics using phase space variables and energy functions, enabling easier analysis of conserved quantities and offering a powerful framework for quantum mechanics.
Action Infographic
 libterm.com
libterm.com