A filtered limit is a concept in category theory that generalizes ordinary limits by allowing the indexing category to be filtered, ensuring existence and good behavior in many mathematical contexts. This property is crucial when studying structures like filtered colimits, which preserve finite limits and connect to important areas such as algebra and topology. Explore the following sections to deepen your understanding of filtered limits and their applications in advanced mathematics.
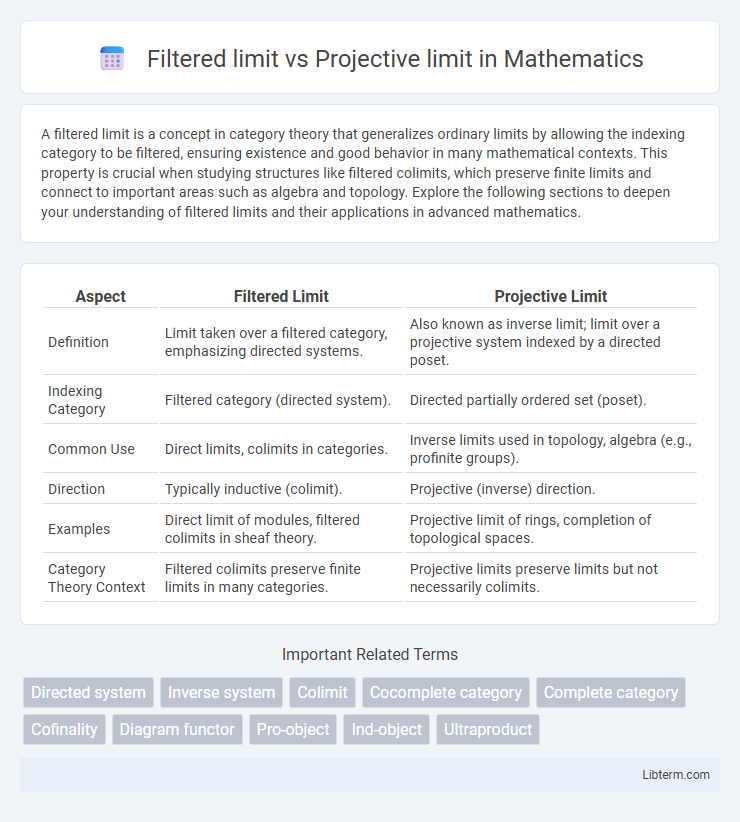
Table of Comparison
| Aspect | Filtered Limit | Projective Limit |
|---|---|---|
| Definition | Limit taken over a filtered category, emphasizing directed systems. | Also known as inverse limit; limit over a projective system indexed by a directed poset. |
| Indexing Category | Filtered category (directed system). | Directed partially ordered set (poset). |
| Common Use | Direct limits, colimits in categories. | Inverse limits used in topology, algebra (e.g., profinite groups). |
| Direction | Typically inductive (colimit). | Projective (inverse) direction. |
| Examples | Direct limit of modules, filtered colimits in sheaf theory. | Projective limit of rings, completion of topological spaces. |
| Category Theory Context | Filtered colimits preserve finite limits in many categories. | Projective limits preserve limits but not necessarily colimits. |
Introduction to Filtered and Projective Limits
Filtered limits arise in category theory as colimits taken over filtered categories, capturing the notion of directed unions or inductive limits. Projective limits, or inverse limits, represent objects constructed as limits over projective systems indexed by filtered partially ordered sets, often encoding solutions to compatible families of morphisms. These constructions play a fundamental role in algebra, topology, and logic by enabling the analysis of structures through their approximations and consistent systems.
Defining Filtered Limits in Category Theory
Filtered limits in category theory are limits taken over a filtered category, where every finite diagram can be extended to a cocone due to the existence of mediating morphisms ensuring coherence. These limits generalize directed colimits and provide a framework for constructing objects by coherently gluing along a filtered diagram, essential for expressing completeness properties in categories such as Set or modules. Filtered limits often preserve finite limits and reflect properties of the underlying category, distinguishing them from general projective limits, which can be defined over arbitrary diagrams without the filteredness constraint.
Understanding Projective (Inverse) Limits
Projective (inverse) limits in category theory construct objects by systematically "inverting" a directed system of objects and morphisms, capturing coherent sequences compatible with projection maps. Unlike filtered limits that focus on direct colimits over filtered categories emphasizing convergence, projective limits emphasize universal properties defined by cones respecting morphism commutativity. Mastery of projective limits is essential for understanding foundational constructions in topology, algebra, and analysis, especially in contexts requiring limits over inverse systems like profinite groups and inverse limits of rings.
Key Differences Between Filtered and Projective Limits
Filtered limits generalize the concept of directed colimits in category theory by considering diagrams indexed over filtered categories, emphasizing the preservation of finite limits in the target category. Projective limits, or inverse limits, focus on diagrams indexed by directed posets and capture objects as limits of inverse systems, often used to construct objects with universal properties. The key difference lies in their indexing categories and universal property orientations: filtered limits arise from cofiltered diagrams emphasizing colimits, while projective limits are specific examples of limits over directed systems that reverse morphism directions.
Common Examples of Filtered Limits
Filtered limits frequently appear in algebraic structures such as direct limits of modules, colimits in category theory, and inductive limits of groups, enabling the construction of objects from directed systems. Projective limits, conversely, arise in inverse limits of topological spaces, profinite groups, and completions in algebraic geometry. Key examples of filtered limits include colimits of directed posets, filtered categories in sheaf theory, and the assembly of vector spaces from finite-dimensional subspaces.
Typical Applications of Projective Limits
Projective limits are commonly applied in number theory for constructing p-adic integers, enabling the study of numbers via inverse systems of modular arithmetic. In algebraic geometry, they allow the definition of schemes as limits of affine schemes, facilitating the analysis of geometric objects through simpler components. Furthermore, projective limits appear in topology to characterize compactness and completeness properties by linking spaces via continuous surjections.
Properties and Characterizations of Filtered Limits
Filtered limits in category theory preserve finite limits and commute with finite products, making them exact in many contexts; they are characterized by diagrams indexed over filtered categories where every finite diagram has a cocone. Unlike projective limits, which are inverse limits over directed sets often used to construct objects from approximations, filtered limits ensure that colimits preserve the injectivity and coherence essential for algebraic and topological structures. The key property of filtered limits is their ability to compute colimits in categories like Set, ensuring that filtered colimits commute with finite limits, a foundational aspect in universal algebra and sheaf theory.
Properties and Characterizations of Projective Limits
Projective limits, also known as inverse limits, are characterized by their universal property that maps any compatible family of morphisms uniquely into the limit object, ensuring a coherent structure across the entire system. They preserve properties such as completeness, compactness, and profinite structures, making them essential in topology, algebra, and category theory. Filtered limits generalize projective limits by focusing on directed systems, but projective limits specifically require a cofiltered (inverse) system, which guarantees the existence of unique mediating morphisms and a richer characterization through limit cones.
Interplay Between Filtered and Projective Limits
The interplay between filtered limits and projective limits centers on the structure of diagrams in category theory, where filtered limits relate to directed systems with cofinality conditions while projective limits correspond to inverse systems over partially ordered sets. Filtered limits often facilitate the preservation of exactness and colimits, contrasting with projective limits that involve inverse limits preserving completeness properties. Understanding their interaction is crucial for analyzing constructions in algebraic geometry, homological algebra, and topology, where filtered colimits and projective limits shape the behavior of sheaves, modules, and complexes.
Summary and Further Reading
Filtered limits generalize inverse limits by allowing indexing over filtered categories, enabling the construction of objects that capture consistent data across directed systems. Projective limits, often synonymous with inverse limits in categories like sets or topological spaces, focus specifically on limits indexed by directed posets, providing a concrete method for "gluing" structures via compatible morphisms. For deeper insights, consult Mac Lane's "Categories for the Working Mathematician" and Borceux's "Handbook of Categorical Algebra" which thoroughly discuss the nuances and categorical implications of filtered and projective limits.
Filtered limit Infographic
 libterm.com
libterm.com