Tensor is a fundamental mathematical object used in physics and engineering to describe multi-dimensional data and relationships. Its applications span from machine learning models to the complex calculations in general relativity, enabling more precise representation of linear mappings and geometric transformations. Explore the rest of the article to discover how tensors can enhance your understanding of advanced scientific concepts.
Table of Comparison
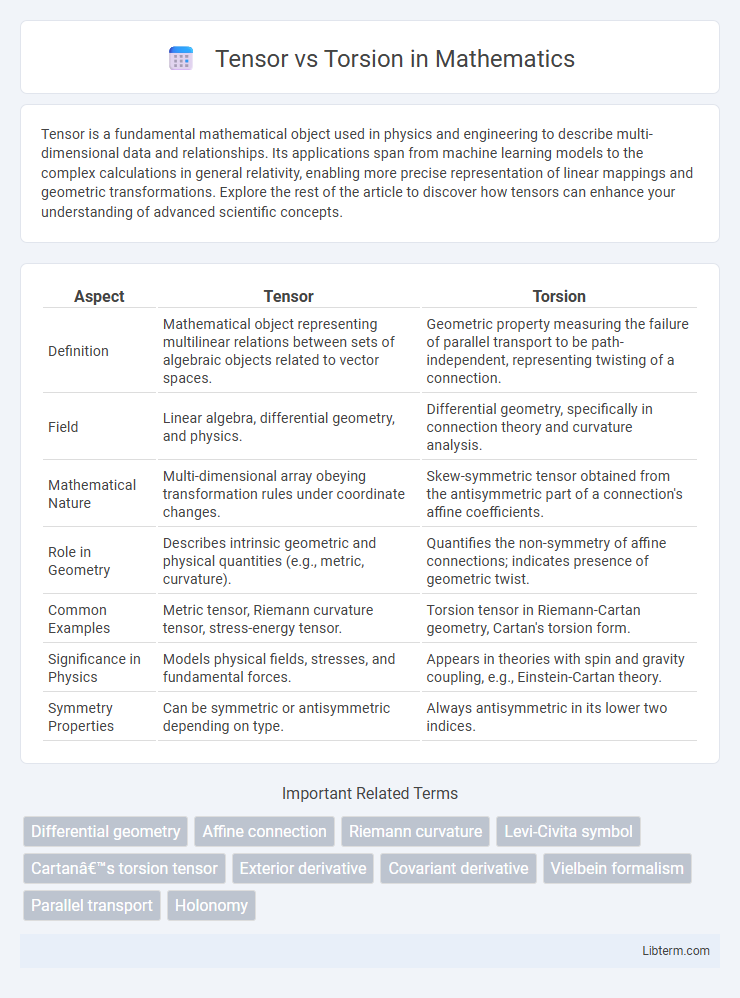
| Aspect | Tensor | Torsion |
|---|---|---|
| Definition | Mathematical object representing multilinear relations between sets of algebraic objects related to vector spaces. | Geometric property measuring the failure of parallel transport to be path-independent, representing twisting of a connection. |
| Field | Linear algebra, differential geometry, and physics. | Differential geometry, specifically in connection theory and curvature analysis. |
| Mathematical Nature | Multi-dimensional array obeying transformation rules under coordinate changes. | Skew-symmetric tensor obtained from the antisymmetric part of a connection's affine coefficients. |
| Role in Geometry | Describes intrinsic geometric and physical quantities (e.g., metric, curvature). | Quantifies the non-symmetry of affine connections; indicates presence of geometric twist. |
| Common Examples | Metric tensor, Riemann curvature tensor, stress-energy tensor. | Torsion tensor in Riemann-Cartan geometry, Cartan's torsion form. |
| Significance in Physics | Models physical fields, stresses, and fundamental forces. | Appears in theories with spin and gravity coupling, e.g., Einstein-Cartan theory. |
| Symmetry Properties | Can be symmetric or antisymmetric depending on type. | Always antisymmetric in its lower two indices. |
Introduction to Tensor and Torsion
Tensors are mathematical objects that generalize scalars, vectors, and matrices, characterized by multi-dimensional arrays used to represent linear relations between geometric vectors, scalars, and other tensors. Torsion refers to the twisting of an object due to applied torque, commonly studied in differential geometry and continuum mechanics, where it measures the rate of change of the angle of rotation along a curve. Understanding tensors is essential for describing physical properties in fields like general relativity, while torsion provides critical insights into material deformation and structural analysis.
Mathematical Definitions of Tensor and Torsion
A tensor is a multilinear mathematical object defined on vector spaces that maps tuples of vectors and covectors to real numbers, generalizing scalars, vectors, and matrices through components that transform linearly under coordinate changes. Torsion, in differential geometry, specifically refers to a tensor associated with an affine connection, measuring the failure of the connection to be symmetric, defined as the antisymmetric part of the connection coefficients or using the torsion tensor \(T(X, Y) = \nabla_X Y - \nabla_Y X - [X, Y]\) for vector fields \(X, Y\). While tensors are broad algebraic entities characterized by transformation rules, torsion is a specific tensor capturing geometric properties of manifolds related to the noncommutativity of covariant derivatives.
Key Differences Between Tensor and Torsion
Tensor represents a multilinear mathematical object used to generalize scalars, vectors, and matrices in physics and engineering, essential in describing physical properties like stress or strain. Torsion specifically refers to the twisting of an object due to applied torque, often analyzed in structural mechanics and materials science to measure deformation along the axis. The key difference lies in their conceptual scope: tensors provide a broad framework for various physical quantities, while torsion is a specific physical phenomenon related to rotational deformation.
Properties and Characteristics of Tensors
Tensors are multi-dimensional arrays that generalize scalars, vectors, and matrices, used to represent linear relations between geometric vectors, scalars, and other tensors in mathematics and physics. Unlike torsion, which describes a twisting deformation in materials or a geometric property in differential geometry, tensors possess defined rank, symmetry, and transformation rules under coordinate changes essential for applications in continuum mechanics and general relativity. The key properties of tensors include multilinearity, invariance under basis transformations, and the ability to encode complex physical phenomena such as stress, strain, and electromagnetic fields.
Properties and Characteristics of Torsion
Torsion describes the twisting of an object due to applied torque, characterized by shear stress and angle of twist along its longitudinal axis. Unlike tensors, which are mathematical entities representing multilinear relationships among vectors, torsion specifically relates to mechanical deformation in materials and structures. Key properties include the torsional rigidity, which depends on the object's geometry and material shear modulus, and the ability to predict failure modes under twisting loads.
Physical Significance in Physics and Engineering
Tensor represents a mathematical object that generalizes scalars, vectors, and matrices, used to describe physical properties such as stress, strain, and moment of inertia in engineering and physics. Torsion specifically refers to the twisting effect experienced by an object when subjected to torque, characterized by shear stress and angle of twist in structural elements like beams and shafts. While tensors provide a comprehensive framework for expressing multi-dimensional physical quantities, torsion is a specific mechanical phenomenon analyzed using tensorial stress and deformation measures.
Applications of Tensors in Various Fields
Tensors serve as foundational tools in multiple fields, including physics, engineering, and computer science, enabling the representation and manipulation of multi-dimensional data crucial for stress analysis, fluid dynamics, and machine learning. Unlike torsion, which specifically describes the twisting of an object around an axis in mechanical contexts, tensors provide a generalized framework for describing linear relations in vector spaces. Applications of tensors span from the stress-strain relationships in materials science to the encoding of geometric properties in general relativity and neural network architectures in artificial intelligence.
Applications of Torsion in Science and Technology
Torsion plays a critical role in engineering disciplines, particularly in mechanics and materials science, where it helps analyze the twisting behavior of shafts and structural elements under applied torques. In medical technology, torsion principles assist in understanding the twisting forces on DNA molecules, influencing genetic research and drug design. Additionally, torsion concepts are vital in geophysics for studying stress and deformation patterns in Earth's crust, aiding earthquake prediction and resource exploration.
Tensor and Torsion in General Relativity
In General Relativity, the tensor primarily used is the metric tensor, which defines the curvature of spacetime and governs the gravitational interaction by relating matter and energy to geometry. Torsion, represented by the torsion tensor, extends the geometric framework by incorporating intrinsic angular momentum (spin) of matter, affecting the connection but is not present in standard General Relativity. Einstein-Cartan theory generalizes General Relativity by including torsion, allowing spacetime to have both curvature and torsion, which influences the dynamics of spinning particles.
Summary and Future Directions
Tensors provide a comprehensive framework in differential geometry by generalizing scalars and vectors, allowing for multidimensional data representation with applications in physics and engineering. Torsion measures the failure of parallel transport to preserve the direction of vectors, playing a crucial role in theories like Einstein-Cartan gravity and material science. Future research aims to unify torsion with quantum gravity models and explore its implications in advanced materials and spacetime topology.
Tensor Infographic
 libterm.com
libterm.com