A simplicial complex is a mathematical concept used in topology and geometry to study shapes and spaces by breaking them down into simpler building blocks called simplices, such as points, line segments, and triangles. This structure allows for an efficient way to analyze complex geometric objects and their properties, particularly in areas like data analysis and mesh generation. Discover how understanding simplicial complexes can enhance your grasp of multi-dimensional shapes by reading the rest of this article.
Table of Comparison
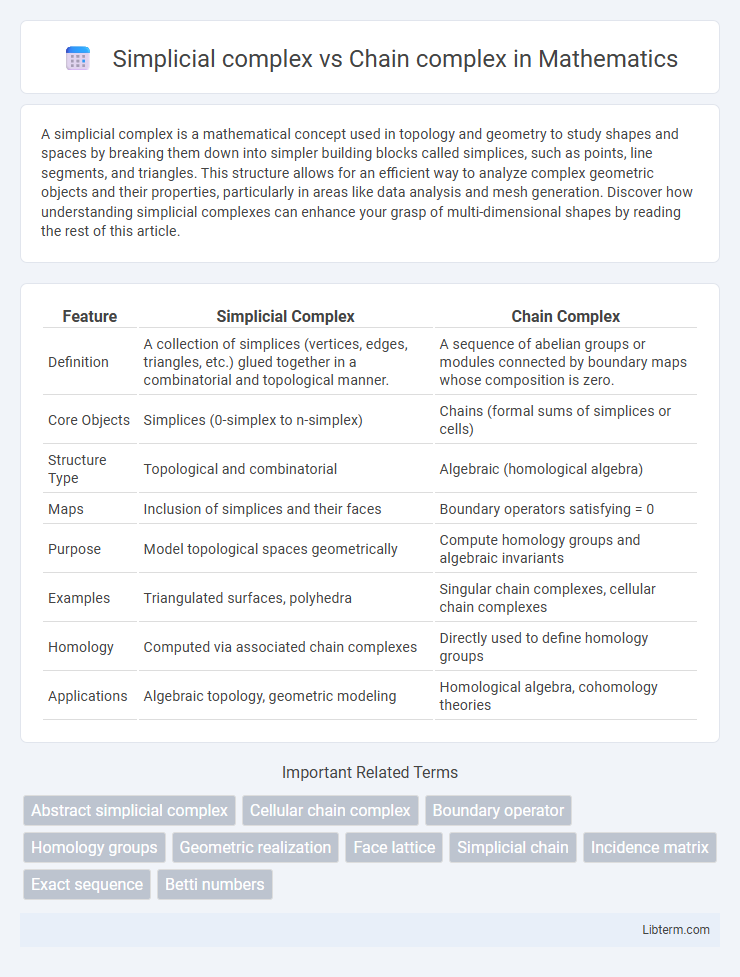
| Feature | Simplicial Complex | Chain Complex |
|---|---|---|
| Definition | A collection of simplices (vertices, edges, triangles, etc.) glued together in a combinatorial and topological manner. | A sequence of abelian groups or modules connected by boundary maps whose composition is zero. |
| Core Objects | Simplices (0-simplex to n-simplex) | Chains (formal sums of simplices or cells) |
| Structure Type | Topological and combinatorial | Algebraic (homological algebra) |
| Maps | Inclusion of simplices and their faces | Boundary operators satisfying = 0 |
| Purpose | Model topological spaces geometrically | Compute homology groups and algebraic invariants |
| Examples | Triangulated surfaces, polyhedra | Singular chain complexes, cellular chain complexes |
| Homology | Computed via associated chain complexes | Directly used to define homology groups |
| Applications | Algebraic topology, geometric modeling | Homological algebra, cohomology theories |
Introduction to Simplicial and Chain Complexes
Simplicial complexes consist of vertices, edges, triangles, and higher-dimensional simplices organized to capture topological structure through their geometric arrangement. Chain complexes are algebraic structures composed of abelian groups or modules connected by boundary operators, encoding relations between simplices via sequences of homomorphisms. Understanding simplicial complexes provides the geometric foundation, while chain complexes translate this geometry into algebraic data for homology computations.
Defining Simplicial Complexes
Simplicial complexes are defined as collections of simplices--vertices, edges, triangles, and higher-dimensional analogues--assembled to form a topological space, adhering to the rule that every face of a simplex is also included in the complex. Chain complexes, in contrast, are algebraic structures consisting of sequences of abelian groups connected by boundary operators, used to compute homology groups of topological spaces, including those represented by simplicial complexes. The fundamental difference lies in simplicial complexes providing a combinatorial-geometric framework, while chain complexes serve as algebraic tools derived from simplicial complexes to analyze topological properties.
Defining Chain Complexes
A chain complex is a sequence of abelian groups or modules connected by boundary operators, where the composition of two consecutive boundary maps equals zero, enabling the study of homology. In contrast, a simplicial complex is a combinatorial structure made up of simplices (vertices, edges, triangles) that defines a topological space, which can be translated into a chain complex by assigning chains to these simplices. Defining chain complexes involves specifying the groups and boundary maps that satisfy the key condition 2 = 0, facilitating algebraic tools for topological analysis.
Key Components and Terminology
Simplicial complexes consist of vertices, edges, triangles, and higher-dimensional simplices organized by inclusion, representing topological spaces through combinatorial structures. Chain complexes are sequences of abelian groups or modules connected by boundary operators, encoding algebraic relationships between these simplices via chain groups and boundary maps. Key terms for simplicial complexes include simplices and faces, while chain complexes focus on chains, boundary operators, and homology groups.
Relationships between Simplicial and Chain Complexes
Simplicial complexes consist of simplices such as vertices, edges, and higher-dimensional faces, organized in a combinatorial structure that captures topological spaces. Chain complexes arise from simplicial complexes by associating abelian groups or modules to each dimension and defining boundary operators that encode the adjacency and orientation of simplices. The relationship between simplicial and chain complexes is fundamental in algebraic topology, as simplicial chain complexes enable computation of homology groups, linking geometric intuition to algebraic invariants.
Comparing Structures and Properties
Simplicial complexes consist of vertices, edges, triangles, and higher-dimensional simplices arranged to form a topological space, emphasizing combinatorial and geometric structure. Chain complexes are algebraic objects defined by sequences of abelian groups or modules connected by boundary homomorphisms with composition zero, focusing on algebraic relations and homology computation. While simplicial complexes provide geometric intuition and a foundation for defining chain complexes, chain complexes abstract these structures into algebraic terms for studying topological invariants like homology groups.
Applications in Algebraic Topology
Simplicial complexes serve as a fundamental tool for modeling topological spaces in algebraic topology by decomposing spaces into simple building blocks like vertices, edges, and higher-dimensional simplices. Chain complexes arise from these simplicial complexes by assigning algebraic structures, such as groups or modules, to simplices and defining boundary operators that connect these structures, enabling the computation of homology groups. Homology groups derived from chain complexes provide powerful invariants that classify topological spaces, detect holes, and characterize their geometric features in applications ranging from sensor networks to data analysis.
Computational Considerations
Simplicial complexes provide a combinatorial framework ideal for representing topological spaces through simplices, enabling efficient data structures for computation in persistent homology and topological data analysis. Chain complexes, defined algebraically through sequences of abelian groups and boundary operators, offer flexibility for abstract algebraic manipulations but often require more computational resources to manage boundary maps and homology calculations. The choice between simplicial and chain complexes impacts algorithmic complexity, memory usage, and implementation efficiency in computational topology applications.
Advantages and Limitations
Simplicial complexes provide a geometric and combinatorial framework for topological spaces, enabling intuitive visualization and direct computation of homology due to their simple simplex-based structure. Chain complexes, on the other hand, offer greater algebraic flexibility, allowing for broader applications beyond geometric intuition, including more general homological algebra contexts. However, simplicial complexes can be limited by combinatorial complexity in higher dimensions, while chain complexes may lack straightforward geometric interpretation and often require more abstract algebraic machinery.
Conclusion: Choosing Between Simplicial and Chain Complexes
Choosing between simplicial and chain complexes depends largely on the topological space and computational goals. Simplicial complexes provide a combinatorial approach well-suited for geometric data and explicit triangulations, offering intuitive visualization and straightforward homology computation. Chain complexes, with their abstract algebraic framework, allow greater flexibility for generalized spaces and facilitate advanced algebraic manipulations in homological algebra and category theory contexts.
Simplicial complex Infographic
 libterm.com
libterm.com