Cardinality refers to the number of elements in a set or the uniqueness of values in a database column, playing a crucial role in data analysis and optimization. Understanding cardinality helps improve query performance and ensures accurate data modeling in various applications. Explore the full article to deepen your grasp of cardinality and enhance your data management skills.
Table of Comparison
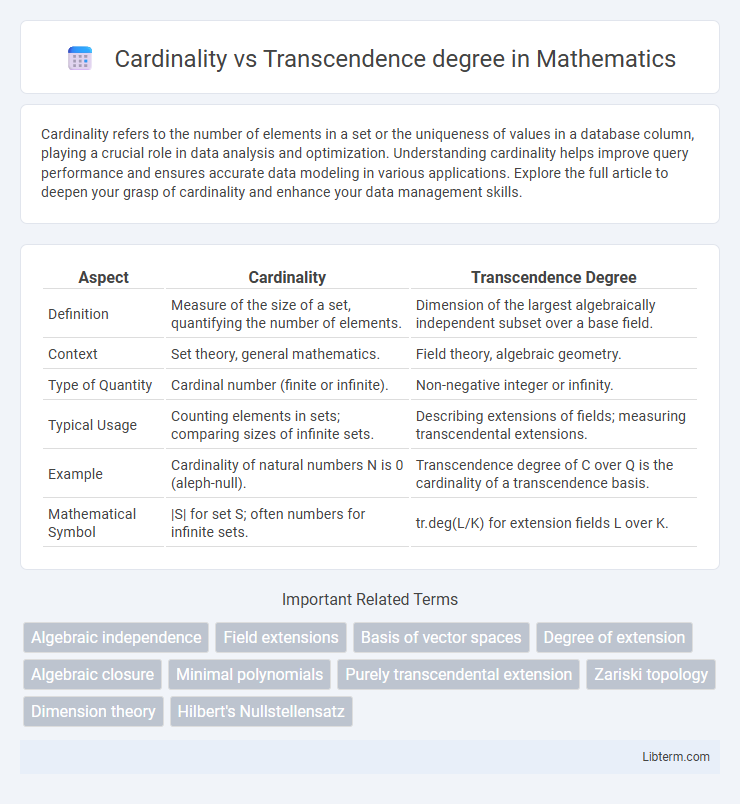
| Aspect | Cardinality | Transcendence Degree |
|---|---|---|
| Definition | Measure of the size of a set, quantifying the number of elements. | Dimension of the largest algebraically independent subset over a base field. |
| Context | Set theory, general mathematics. | Field theory, algebraic geometry. |
| Type of Quantity | Cardinal number (finite or infinite). | Non-negative integer or infinity. |
| Typical Usage | Counting elements in sets; comparing sizes of infinite sets. | Describing extensions of fields; measuring transcendental extensions. |
| Example | Cardinality of natural numbers N is 0 (aleph-null). | Transcendence degree of C over Q is the cardinality of a transcendence basis. |
| Mathematical Symbol | |S| for set S; often numbers for infinite sets. | tr.deg(L/K) for extension fields L over K. |
Introduction to Cardinality and Transcendence Degree
Cardinality measures the size of a set, quantifying the number of elements, while transcendence degree assesses the size of a field extension in terms of the number of algebraically independent transcendental elements. In field theory, transcendence degree indicates how far an extension field is from being algebraic, providing a crucial invariant for comparing field extensions. Understanding cardinality and transcendence degree is essential for studying structures in algebra and their dimensional properties.
Fundamental Concepts: Sets, Fields, and Extensions
Cardinality measures the size of sets by counting the number of elements, fundamental in set theory, while transcendence degree evaluates the size of field extensions by counting algebraically independent elements over a base field. In field theory, an extension field E over a base field F is analyzed through its transcendence degree, which reflects how many elements of E are transcendental over F, contrasting with algebraic extensions where the transcendence degree is zero. Understanding these concepts is crucial for distinguishing between finite cardinality sets, algebraic extensions with no transcendence, and transcendental extensions characterized by infinite or finite transcendence degrees, bridging set theory and field theory in algebraic structures.
Defining Cardinality: Measuring Set Size
Cardinality quantifies the size of a set by establishing a one-to-one correspondence between its elements and natural numbers, allowing comparison of infinite sets through bijections. In contrast, transcendence degree measures the size of a field extension by counting the maximal algebraically independent subset over the base field. Defining cardinality as a foundational tool enables classification of sets into countable and uncountable, providing a rigorous framework for understanding infinite collections in set theory.
What is Transcendence Degree?
Transcendence degree measures the size of the largest algebraically independent subset over a base field within a field extension, providing a key invariant in field theory. It quantifies how many transcendental elements, which are not roots of any nonzero polynomial with coefficients in the base field, exist in the extension. Unlike cardinality, which counts the total number of elements, transcendence degree captures the minimal algebraic complexity needed to generate the extension.
Cardinality in Algebraic and Transcendental Extensions
Cardinality in algebraic extensions refers to the size of the set of algebraic elements over a base field, which is generally countable when the base field is countable due to algebraic elements being roots of polynomials with coefficients in that field. In transcendental extensions, cardinality often becomes uncountable because transcendental elements are not roots of any polynomial over the base field, leading to infinitely many algebraically independent elements. The distinction between algebraic and transcendental extensions is critical for understanding the structure and dimension of field extensions, where transcendence degree measures the maximal number of algebraically independent transcendental elements, while cardinality considers the overall size of these sets.
Comparing Roles: Cardinality vs. Transcendence Degree
Cardinality measures the size of a set, reflecting the number of elements, while transcendence degree quantifies the maximal number of algebraically independent elements in a field extension. Cardinality provides a global count of elements, essential for understanding set size and comparing infinite sets, whereas transcendence degree captures the algebraic complexity and independence within field extensions. Both concepts are crucial in algebra and set theory, with cardinality addressing quantity and transcendence degree highlighting structural independence.
Mathematical Examples and Applications
Cardinality measures the size of sets, such as the infinite cardinality of the real numbers \(\mathbb{R}\) compared to the countable infinity of the integers \(\mathbb{Z}\), while transcendence degree quantifies the maximal number of algebraically independent elements over a base field, critical in field extensions like \(\mathbb{C}/\mathbb{Q}\). In algebraic geometry, transcendence degree identifies the dimension of varieties, with the function field's transcendence degree over \(\mathbb{C}\) equating to the variety's dimension, contrasting with cardinality which does not capture algebraic structure. Applications include classifying fields in Galois theory, where transcendence degree distinguishes purely transcendental extensions, and analyzing infinite sets in set theory, where cardinality differentiates levels of infinity such as countable vs. uncountable sets.
Interplay in Field Theory
The interplay between cardinality and transcendence degree in field theory crucially shapes the structure of field extensions, with transcendence degree measuring the size of maximal algebraically independent subsets, while cardinality quantifies the overall set size. In algebraic extensions, finite transcendence degree correlates with countable cardinalities, whereas infinite transcendence degree can produce uncountable cardinalities emphasizing the complexity of extension fields. Understanding this relationship facilitates classification of extensions, impacting algebraic geometry, model theory, and the study of function fields over various base fields.
Importance in Algebra and Beyond
Cardinality measures the size of a set, essential for understanding infinite structures and comparing their magnitudes in algebra and set theory. Transcendence degree quantifies the number of algebraically independent elements over a base field, critical for analyzing field extensions, algebraic independence, and function fields in algebraic geometry. Both concepts underpin the classification of algebraic structures, influence dimension theory, and extend applications in number theory, model theory, and complex analysis.
Conclusion: When to Use Each Concept
Cardinality measures the size of a set, useful for comparing infinite sets or analyzing cardinalities in set theory. Transcendence degree quantifies the algebraic independence of elements over a base field, critical in field extensions and algebraic geometry. Use cardinality when dealing with quantitative size and set comparisons, and transcendence degree when assessing algebraic complexity and independence within field theory.
Cardinality Infographic
 libterm.com
libterm.com