The normal bundle is a fundamental concept in differential geometry, describing how a submanifold sits inside a larger manifold by capturing directions perpendicular to the submanifold. Understanding its structure can reveal important geometric and topological properties that influence curvature and stability analyses. Discover how the normal bundle plays a crucial role in your study by exploring the detailed explanations in this article.
Table of Comparison
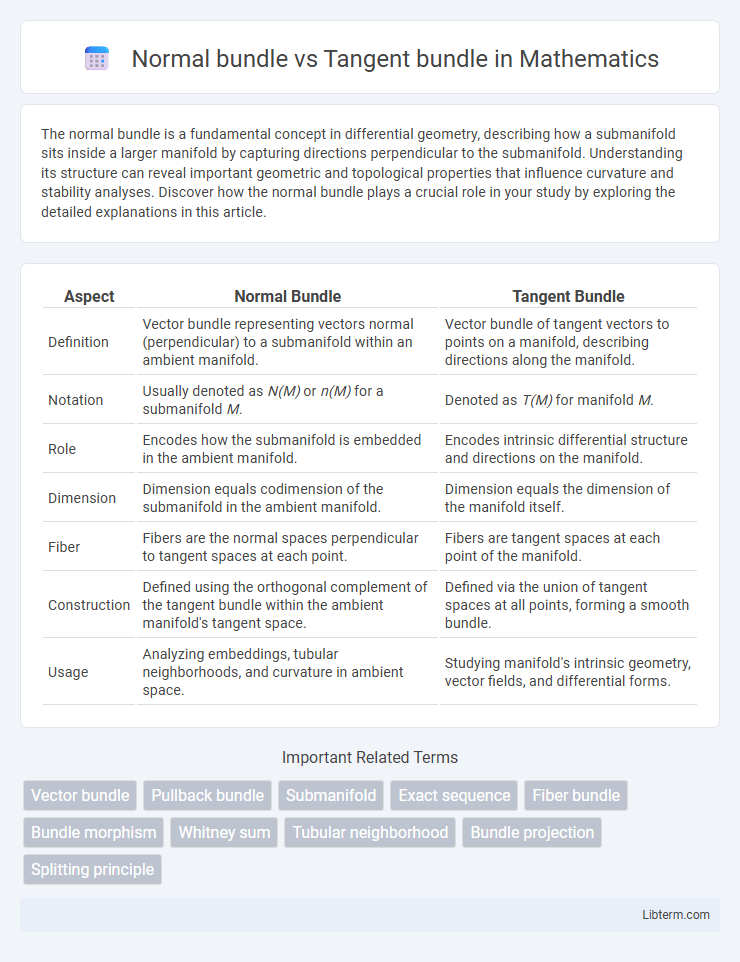
| Aspect | Normal Bundle | Tangent Bundle |
|---|---|---|
| Definition | Vector bundle representing vectors normal (perpendicular) to a submanifold within an ambient manifold. | Vector bundle of tangent vectors to points on a manifold, describing directions along the manifold. |
| Notation | Usually denoted as N(M) or n(M) for a submanifold M. | Denoted as T(M) for manifold M. |
| Role | Encodes how the submanifold is embedded in the ambient manifold. | Encodes intrinsic differential structure and directions on the manifold. |
| Dimension | Dimension equals codimension of the submanifold in the ambient manifold. | Dimension equals the dimension of the manifold itself. |
| Fiber | Fibers are the normal spaces perpendicular to tangent spaces at each point. | Fibers are tangent spaces at each point of the manifold. |
| Construction | Defined using the orthogonal complement of the tangent bundle within the ambient manifold's tangent space. | Defined via the union of tangent spaces at all points, forming a smooth bundle. |
| Usage | Analyzing embeddings, tubular neighborhoods, and curvature in ambient space. | Studying manifold's intrinsic geometry, vector fields, and differential forms. |
Introduction to Vector Bundles
Vector bundles generalize the concept of vector spaces by assigning a vector space to each point of a manifold, with the tangent bundle encompassing all tangent spaces that describe directions on the manifold. The normal bundle, on the other hand, captures the complementary vector spaces orthogonal to a given submanifold's tangent spaces within an ambient manifold. Understanding the distinction between tangent bundles and normal bundles is essential for studying differential geometry and analyzing how submanifolds sit inside higher-dimensional spaces.
Defining the Tangent Bundle
The tangent bundle of a smooth manifold \(M\) is the disjoint union of all tangent spaces \(T_xM\) at each point \(x \in M\), forming a smooth vector bundle over \(M\). It encodes directional derivatives and velocities of curves on the manifold, providing a global geometric framework for differential calculus. Unlike the normal bundle, which describes vectors orthogonal to a submanifold within an ambient space, the tangent bundle intrinsically captures all tangent directions within the manifold itself.
Exploring the Normal Bundle
The normal bundle of a submanifold captures the orthogonal directions to the tangent bundle within the ambient manifold, providing insight into the geometry and curvature of the embedding. It consists of vectors normal to the submanifold at each point, complementing the tangent space and facilitating the study of deformation and stability properties. Understanding the normal bundle is crucial for analyzing submanifold embeddings, mean curvature flow, and related geometric phenomena.
Key Differences: Tangent vs Normal Bundles
The tangent bundle of a differentiable manifold consists of all tangent vectors at every point, forming a vector bundle that encodes directional derivatives and geometric structure. In contrast, the normal bundle is defined for a submanifold and consists of vectors in the ambient manifold orthogonal to the tangent space, capturing the extrinsic curvature information. Key differences lie in their roles: tangent bundles describe intrinsic geometry, while normal bundles describe how a submanifold sits inside a higher-dimensional manifold.
Geometric Interpretation of Each Bundle
The tangent bundle of a manifold consists of all tangent vectors at every point, representing directions in which one can tangentially move within the manifold. The normal bundle, defined for a submanifold embedded in a higher-dimensional manifold, comprises vectors perpendicular to the tangent space, capturing directions normal to the submanifold. Geometrically, the tangent bundle encodes intrinsic movement along the manifold, while the normal bundle characterizes the embedding's extrinsic geometry through normal displacement vectors.
Applications in Differential Geometry
The tangent bundle captures all possible directions on a manifold, making it essential for studying vector fields, differential equations, and curvature. The normal bundle complements this by describing directions orthogonal to a submanifold within an ambient manifold, crucial for embedding problems and analyzing geometric deformations. Applications in differential geometry leverage the interplay between tangent and normal bundles to understand shape, stability, and intersections of submanifolds in various geometric contexts.
Role in Submanifold Theory
The tangent bundle of a submanifold captures all tangent vectors at each point, representing directions intrinsic to the submanifold itself. The normal bundle, in contrast, consists of vectors orthogonal to the submanifold within the ambient manifold, serving to describe how the submanifold is embedded and its extrinsic geometry. These bundles jointly facilitate the study of curvature, embedding properties, and deformation theory in submanifold theory.
Visualizing Tangent and Normal Bundles
Visualizing tangent bundles involves imagining all tangent vectors attached smoothly to each point of a manifold, forming a higher-dimensional space that encapsulates directional derivatives. The normal bundle complements this by representing vectors perpendicular to the manifold, essential for describing how the manifold sits inside an ambient space. Understanding the interaction between tangent and normal bundles aids in grasping geometric properties, curvature, and embedding characteristics of manifolds.
Examples in Mathematics and Physics
The tangent bundle of a smooth manifold consists of all tangent vectors at every point and is fundamental in differential geometry, exemplified by the tangent bundle of a sphere used to study geodesics and curvature. The normal bundle, in contrast, describes vectors perpendicular to a submanifold within a higher-dimensional manifold, such as the normal bundle of a curve embedded in Euclidean space, crucial in the analysis of extrinsic curvature and surface deformation. In physics, tangent bundles underlie the phase space formulation of classical mechanics, while normal bundles appear in general relativity to analyze the embedding of lower-dimensional branes in higher-dimensional spacetimes.
Summary and Comparative Insights
The tangent bundle of a smooth manifold consists of all tangent vectors at every point, representing directions along the manifold, whereas the normal bundle captures vectors orthogonal to the manifold within an ambient space. Tangent bundles play a crucial role in differential geometry and vector fields, while normal bundles are fundamental in understanding embeddings, curvature, and submanifold geometry. Comparing both, tangent bundles describe intrinsic properties of manifolds, whereas normal bundles provide extrinsic geometric information relative to the embedding space.
Normal bundle Infographic
 libterm.com
libterm.com