The nerve complex is a critical network of interconnected neurons responsible for transmitting signals throughout the body, ensuring proper communication between the brain and various organs. Understanding the structure and function of your nerve complex can help in identifying neurological disorders and improving overall nervous system health. Explore the full article to learn how the nerve complex influences your daily life and well-being.
Table of Comparison
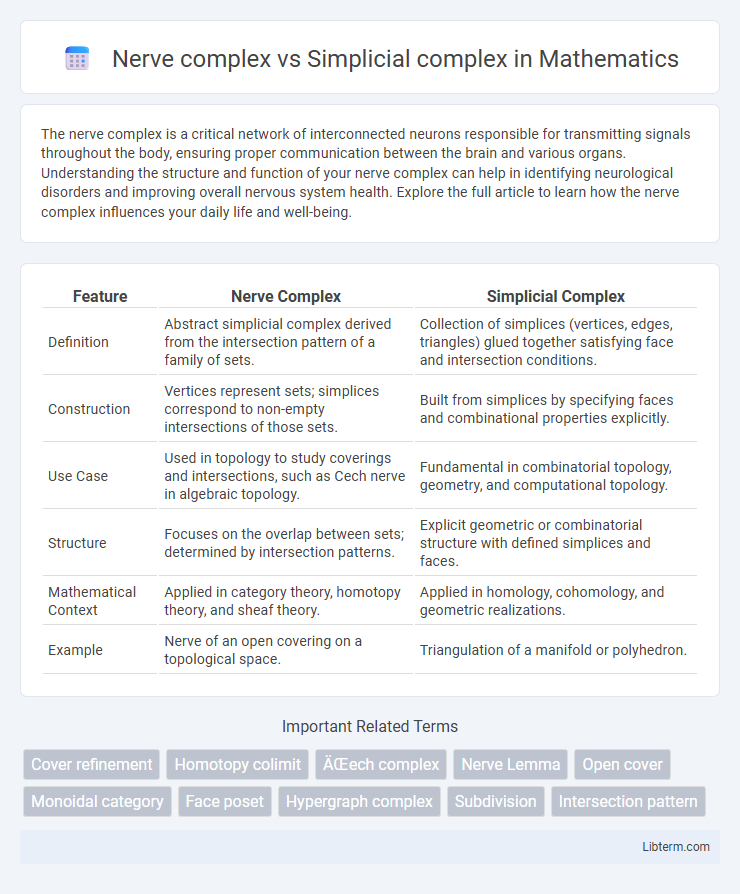
| Feature | Nerve Complex | Simplicial Complex |
|---|---|---|
| Definition | Abstract simplicial complex derived from the intersection pattern of a family of sets. | Collection of simplices (vertices, edges, triangles) glued together satisfying face and intersection conditions. |
| Construction | Vertices represent sets; simplices correspond to non-empty intersections of those sets. | Built from simplices by specifying faces and combinational properties explicitly. |
| Use Case | Used in topology to study coverings and intersections, such as Cech nerve in algebraic topology. | Fundamental in combinatorial topology, geometry, and computational topology. |
| Structure | Focuses on the overlap between sets; determined by intersection patterns. | Explicit geometric or combinatorial structure with defined simplices and faces. |
| Mathematical Context | Applied in category theory, homotopy theory, and sheaf theory. | Applied in homology, cohomology, and geometric realizations. |
| Example | Nerve of an open covering on a topological space. | Triangulation of a manifold or polyhedron. |
Introduction to Nerve Complexes and Simplicial Complexes
Nerve complexes are formed from a family of sets by encoding the pattern of intersections as simplices, providing a combinatorial structure that captures the underlying topology of a cover. Simplicial complexes consist of vertices, edges, triangles, and their higher-dimensional counterparts arranged to model and study the shape and connectivity of spaces in algebraic topology. Understanding the relationship between nerve complexes and simplicial complexes is fundamental in applied topology, enabling the analysis of complex data through intersection patterns and simplicial constructions.
Historical Background and Mathematical Foundations
Nerve complexes originated from Alexandroff's work in the 1920s, providing a combinatorial tool to study topological spaces via covers, focusing on the intersection patterns of open sets. Simplicial complexes trace back to Poincare's early 20th-century studies in algebraic topology, representing spaces through simplices glued along faces, enabling combinatorial and geometric analyses. Both frameworks underpin modern topological data analysis, with nerve complexes emphasizing categorical covers and simplicial complexes emphasizing geometric decompositions.
Definitions: What is a Simplicial Complex?
A simplicial complex is a topological space constructed from simplices, such as points, line segments, triangles, and higher-dimensional analogues, assembled in a manner that satisfies two conditions: every face of a simplex is also in the complex, and the intersection of any two simplices is either empty or a shared face. Each simplex in the complex represents a set of vertices, making the structure ideal for encoding combinatorial and geometric relationships. Simplicial complexes serve as a fundamental tool in algebraic topology, enabling the study of shapes and spaces through discrete combinatorial data.
Definitions: What is a Nerve Complex?
A nerve complex is a simplicial complex constructed from a family of sets by assigning a simplex to every finite subcollection of sets with a nonempty intersection. It captures the combinatorial structure of how sets overlap, encoding intersection patterns as simplices. This concept is fundamental in algebraic topology for analyzing covers and their associated topologies.
Topological Properties of Simplicial Complexes
Simplicial complexes exhibit robust topological properties derived from their combinatorial structure, enabling the calculation of homology groups which reveal connectivity and holes within the space. Unlike nerve complexes, which are constructed from open covers and may lack simplicial structure, simplicial complexes guarantee finite intersections and well-defined simplices, facilitating algebraic topology tools such as the Mayer-Vietoris sequence. These properties make simplicial complexes fundamental in computational topology for persistent homology and topological data analysis applications.
Structural Characteristics of Nerve Complexes
Nerve complexes are constructed from a family of sets, where each simplex corresponds to a non-empty intersection of these sets, resulting in a combinatorial structure that captures the overlap patterns of the underlying collection. Unlike simplicial complexes, which are defined purely by abstract simplices and their faces, nerve complexes encode topological and intersectional information directly tied to the underlying sets, making them useful in applications like algebraic topology and data analysis. The structural characteristic of nerve complexes lies in their representation of intersections, leading to a complex that can reveal higher-order connectivity and coverage properties of the original set family.
Key Differences Between Nerve and Simplicial Complexes
Nerve complexes are constructed from a cover of sets where simplices correspond to non-empty intersections of these sets, while simplicial complexes are abstract collections of simplices defined by vertices and their subsets. The nerve complex inherently encodes the topological relationships of the cover through intersection patterns, whereas simplicial complexes provide a combinatorial framework modeling topological spaces via simplices connected through faces. Key differences include the origin of construction--nerve complexes arise from covers of spaces, and simplicial complexes arise from abstract simplex assemblies--and their applications, with nerve complexes often used in topology and data analysis to capture cover intersections, contrasting with simplicial complexes' broader use in combinatorial topology.
Applications in Topological Data Analysis
Nerve complexes and simplicial complexes serve distinct roles in topological data analysis (TDA), with nerve complexes often used to capture the intersection patterns of covers that aid in reconstructing the shape of data from overlapping regions. Simplicial complexes, such as Vietoris-Rips or Cech complexes, provide a combinatorial framework to approximate the underlying topology of point cloud data by building simplices based on proximity or intersection criteria. In practical applications, nerve complexes excel in analyzing clustered or overlapping datasets by representing cover relationships, while simplicial complexes offer scalable computational methods for identifying homological features like loops and voids in high-dimensional data.
Computational Aspects and Algorithmic Considerations
Nerve complexes enable efficient topological data analysis by representing intersections of cover sets, reducing computational complexity in high-dimensional data processing. Simplicial complexes, constructed from simplices like vertices, edges, and triangles, offer flexible data representation but often involve higher computational overhead due to explicit simplex enumeration. Algorithmic considerations favor nerve complexes for sparse data sampling where computational efficiency and scalability are critical, whereas simplicial complexes provide detailed combinatorial structures essential for fine-grained homological computations.
Future Trends and Research Directions
Emerging research in topological data analysis increasingly explores the computational efficiency and scalability of nerve complexes compared to simplicial complexes in high-dimensional data. Future trends emphasize leveraging nerve complexes for multi-scale representations and persistent homology due to their reduced combinatorial complexity, facilitating improved algorithms in machine learning and data science. Integrating nerve complex frameworks with advancements in neural networks and algebraic topology is anticipated to drive new methodologies for analyzing complex datasets in bioinformatics, sensor networks, and geometric deep learning.
Nerve complex Infographic
 libterm.com
libterm.com