Fractal dimension quantifies the complexity of shapes and patterns that exhibit self-similarity at different scales, offering insights into structures that traditional geometry cannot measure. This concept is widely applied in fields such as physics, biology, and finance to analyze irregular objects or phenomena, from coastline shapes to market fluctuations. Explore the full article to understand how fractal dimension can enhance your analysis of complex systems.
Table of Comparison
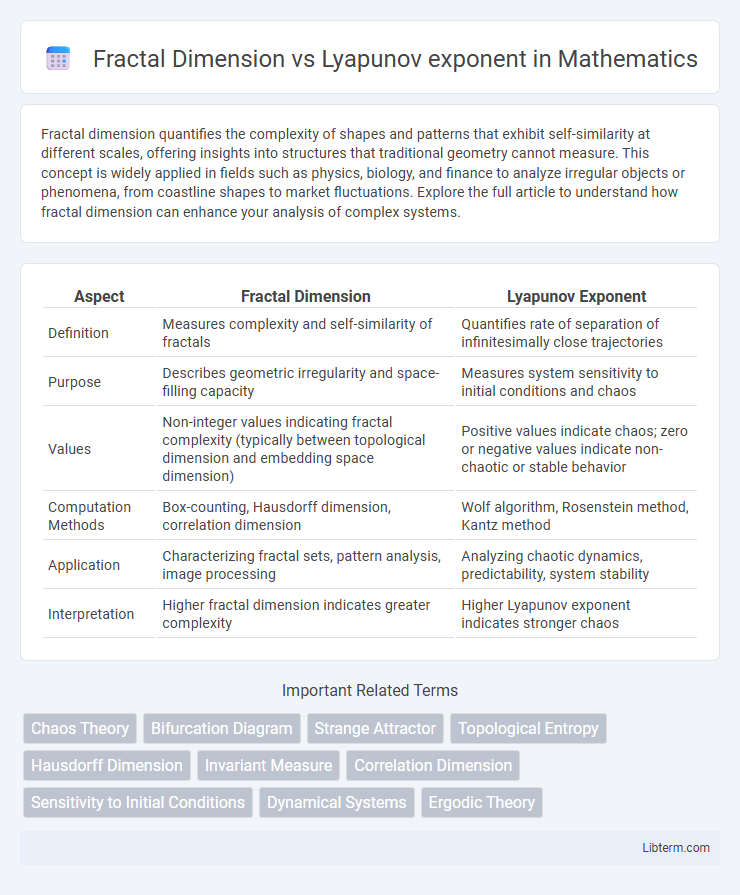
| Aspect | Fractal Dimension | Lyapunov Exponent |
|---|---|---|
| Definition | Measures complexity and self-similarity of fractals | Quantifies rate of separation of infinitesimally close trajectories |
| Purpose | Describes geometric irregularity and space-filling capacity | Measures system sensitivity to initial conditions and chaos |
| Values | Non-integer values indicating fractal complexity (typically between topological dimension and embedding space dimension) | Positive values indicate chaos; zero or negative values indicate non-chaotic or stable behavior |
| Computation Methods | Box-counting, Hausdorff dimension, correlation dimension | Wolf algorithm, Rosenstein method, Kantz method |
| Application | Characterizing fractal sets, pattern analysis, image processing | Analyzing chaotic dynamics, predictability, system stability |
| Interpretation | Higher fractal dimension indicates greater complexity | Higher Lyapunov exponent indicates stronger chaos |
Introduction to Fractal Dimension and Lyapunov Exponent
Fractal dimension quantifies the complexity of geometrical shapes by measuring how detail changes with scale, revealing patterns in chaotic systems. The Lyapunov exponent evaluates the rate at which nearby trajectories in a dynamical system diverge, indicating system sensitivity to initial conditions and predictability. Together, these metrics offer critical insights into chaos theory by characterizing structural intricacies and dynamic stability of nonlinear systems.
Defining Fractal Dimension: Quantifying Complexity
Fractal dimension quantifies complexity by measuring how detail in a pattern changes with scale, capturing the space-filling capacity of fractal structures. It provides a numerical value that indicates the degree of irregularity or fragmentation in a geometric object, distinguishing simple shapes from intricate, self-similar patterns. Unlike the Lyapunov exponent, which assesses sensitivity to initial conditions in dynamical systems, fractal dimension focuses on spatial complexity and scaling properties of fractal sets.
Understanding the Lyapunov Exponent: Measuring Chaos
The Lyapunov exponent quantifies the rate of separation of infinitesimally close trajectories, serving as a critical measure of chaos in dynamic systems. A positive Lyapunov exponent indicates sensitive dependence on initial conditions, characteristic of chaotic behavior, while a negative or zero value signifies stable or periodic dynamics. Unlike the fractal dimension, which describes the geometric complexity of attractors, the Lyapunov exponent captures temporal unpredictability and system stability through exponential divergence rates.
Mathematical Foundations of Fractal Dimension
Fractal dimension quantifies the complexity of geometric shapes by measuring how detail in a pattern changes with scale, rooted in concepts such as self-similarity and scaling laws. Its mathematical foundation relies on methods like box-counting, Hausdorff dimension, and correlation dimension, which rigorously define how fractal sets occupy space in non-integer dimensions. Unlike the Lyapunov exponent, which measures the rate of separation of infinitesimally close trajectories in dynamical systems, the fractal dimension captures spatial complexity and scaling behavior intrinsic to fractal geometry.
Lyapunov Exponent: Calculation and Interpretation
The Lyapunov exponent quantifies the rate of separation of infinitesimally close trajectories in a dynamical system, serving as a key indicator of chaos. Calculation involves evaluating the average exponential divergence of nearby trajectories over time, often using algorithms such as the Wolf, Rosenstein, or Kantz methods. A positive Lyapunov exponent signals sensitivity to initial conditions and chaotic behavior, while zero or negative values indicate periodic or stable dynamics.
Key Differences: Fractal Dimension vs Lyapunov Exponent
Fractal dimension measures the complexity and self-similarity of a geometric shape or attractor, quantifying how detail changes with scale, whereas the Lyapunov exponent gauges the rate of separation of infinitesimally close trajectories, indicating system sensitivity to initial conditions and chaos. Fractal dimension is a static, geometrical property often used in characterizing attractors, while the Lyapunov exponent is a dynamic measure that reflects predictability and stability in a system's evolution over time. Both metrics are crucial in chaos theory but serve fundamentally different roles: fractal dimension captures spatial complexity, and the Lyapunov exponent describes temporal divergence.
Applications in Dynamical Systems Analysis
Fractal dimension quantifies the complexity of geometric structures in phase space, enabling the identification of strange attractors and chaotic behavior in dynamical systems. Lyapunov exponent measures the average rates of divergence or convergence of nearby trajectories, providing insights into system stability and predictability. Together, these metrics are crucial in fields such as weather forecasting, financial market analysis, and physiological signal processing, where understanding chaos and stability is essential for model accuracy and control.
Visualizing Patterns: Fractals and Chaotic Attractors
Fractal dimension quantifies the complexity and self-similarity of fractal patterns, measuring how detail changes with scale to visualize intricate geometric structures. Lyapunov exponent evaluates the sensitivity to initial conditions in chaotic systems, indicating exponential divergence and helping to map chaotic attractors' unpredictable behavior. Combined analysis of fractal dimension and Lyapunov exponent enables enhanced visualization of complex dynamic patterns, revealing underlying order within apparent chaos.
Real-world Examples in Science and Engineering
Fractal dimension quantifies the complexity of geometrical structures observed in phenomena such as turbulent fluid flow, geophysical patterns, and material fracture surfaces, providing insights into their spatial scaling behavior. Lyapunov exponent measures the sensitivity to initial conditions in dynamic systems like weather forecasting, electrical circuits, and biological rhythms, indicating chaotic behavior and predictability limits. In engineering, fractal dimensions help optimize porous material design, while Lyapunov exponents guide control system stability and fault detection.
Conclusion: Complementary Tools for System Characterization
Fractal dimension and Lyapunov exponent serve as complementary tools in characterizing complex dynamical systems by quantifying different aspects of their chaotic behavior. While fractal dimension measures the geometric complexity of attractors, Lyapunov exponent assesses the sensitivity to initial conditions and predictability of system trajectories. Combining both metrics provides a more comprehensive understanding of system dynamics, enabling enhanced analysis of stability, chaos, and underlying structure in nonlinear systems.
Fractal Dimension Infographic
 libterm.com
libterm.com