A Pushdown Automaton (PDA) is a computational model that extends finite automata capabilities by utilizing a stack to handle context-free languages. It operates by reading input symbols and managing stack operations, enabling it to recognize patterns beyond regular languages. Discover how a Pushdown Automaton functions and its applications in computational theory in the following sections.
Table of Comparison
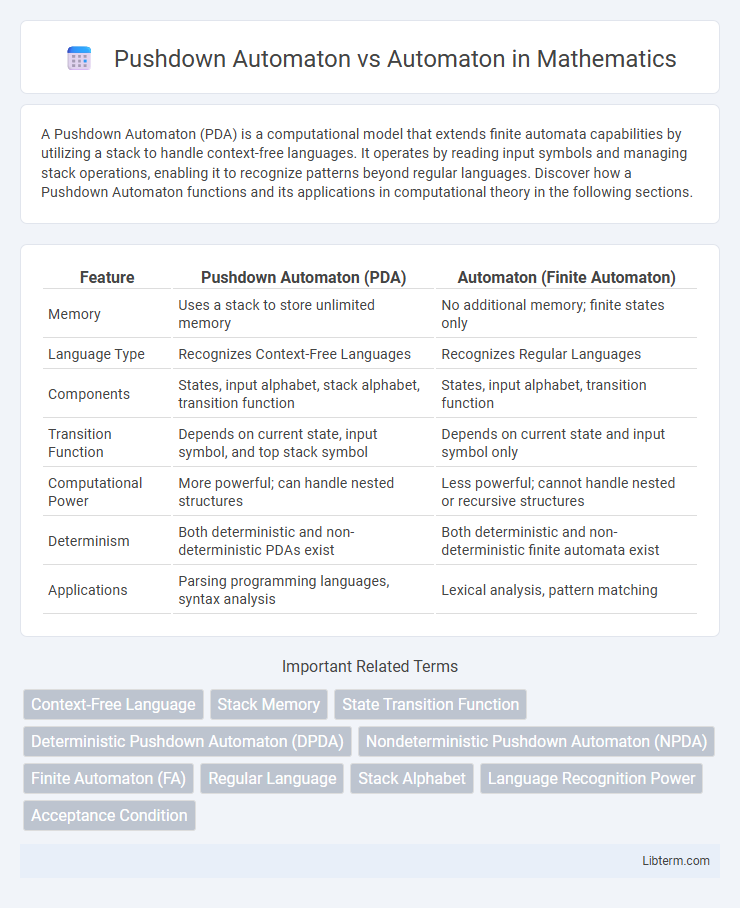
| Feature | Pushdown Automaton (PDA) | Automaton (Finite Automaton) |
|---|---|---|
| Memory | Uses a stack to store unlimited memory | No additional memory; finite states only |
| Language Type | Recognizes Context-Free Languages | Recognizes Regular Languages |
| Components | States, input alphabet, stack alphabet, transition function | States, input alphabet, transition function |
| Transition Function | Depends on current state, input symbol, and top stack symbol | Depends on current state and input symbol only |
| Computational Power | More powerful; can handle nested structures | Less powerful; cannot handle nested or recursive structures |
| Determinism | Both deterministic and non-deterministic PDAs exist | Both deterministic and non-deterministic finite automata exist |
| Applications | Parsing programming languages, syntax analysis | Lexical analysis, pattern matching |
Introduction to Automata Theory
Pushdown Automata (PDA) extend finite automata by incorporating a stack, enabling them to recognize context-free languages beyond the capabilities of regular finite automata. While finite automata process input strings with a fixed amount of memory, PDAs utilize their stack to keep track of nested structures and recursive patterns, essential in parsing programming languages. The distinction is a foundational concept in Automata Theory, illustrating the hierarchy of language classes and computational power between regular and context-free languages.
What is an Automaton?
An automaton is a mathematical model of computation that consists of states, transitions, and inputs used to recognize patterns within input strings. Unlike a pushdown automaton which uses a stack for memory, a basic automaton such as a finite automaton lacks auxiliary memory structures and operates solely based on its current state. Automata serve as foundational tools in formal language theory, compiler design, and parsing algorithms.
Overview of Pushdown Automaton (PDA)
Pushdown Automaton (PDA) extends the capabilities of a finite automaton by incorporating a stack-based memory, enabling it to recognize context-free languages. Unlike standard automata, which have limited memory, PDAs use the stack to handle nested structures such as balanced parentheses or recursive patterns. This additional memory makes PDAs essential in parsing and syntax analysis in compiler design.
Key Differences Between Automaton and Pushdown Automaton
A Pushdown Automaton (PDA) differs from a finite Automaton by incorporating a stack, which enables it to recognize context-free languages, whereas finite Automata recognize only regular languages. The stack in a PDA provides additional memory to handle nested structures and recursive patterns, essential for parsing programming languages and expressions. Unlike Automata, which have limited memory and state transitions, PDAs use their stack to manage and process an unlimited amount of information dynamically.
State and Memory Comparison
Pushdown Automata (PDA) differ from finite Automata primarily in their use of memory and state management; PDAs incorporate a stack allowing them to recognize context-free languages, whereas finite Automata use a finite set of states without auxiliary memory for only regular languages. The stack in PDA provides dynamic memory that stores an unbounded amount of information, enabling the machine to handle nested structures by pushing and popping symbols, while finite Automata rely solely on state transitions with fixed memory. This difference in memory fundamentally expands the computational power of PDAs beyond the capabilities of finite Automata, making PDAs suitable for parsing programming languages and expressions.
Language Recognition Capabilities
Pushdown Automata (PDA) extend finite automata by incorporating a stack, enabling them to recognize context-free languages, such as balanced parentheses and nested structures, which standard finite automata cannot process. Finite automata are limited to recognizing regular languages, characterized by simpler patterns without nested dependencies. The stack in PDAs provides memory for tracking hierarchical language constructs, significantly expanding their language recognition capabilities beyond the reach of traditional automata.
Use Cases of Finite Automata
Finite automata are primarily used in lexical analysis, pattern matching, and simple text processing due to their ability to recognize regular languages. Pushdown automata extend finite automata with a stack, enabling them to parse context-free languages such as programming language syntax and nested structures. Use cases of finite automata include tokenizing input in compilers, validating strings against regular expressions, and protocol verification in networking.
Applications of Pushdown Automata
Pushdown Automata (PDA) are essential in parsing and recognizing context-free languages, making them crucial for compiler design and syntax analysis in programming languages. Unlike finite automata, PDAs utilize a stack to manage nested structures such as parentheses and recursive patterns, enabling the processing of more complex language constructs. Applications of PDAs extend to natural language processing, where context-free grammar models are required for sentence structure analysis and language translation tasks.
Limitations and Strengths of Each Model
Pushdown Automata (PDA) extend finite automata by incorporating a stack, enabling them to recognize context-free languages, which finite automata cannot; however, PDAs are limited in processing context-sensitive languages due to their single stack memory. Finite automata are efficient and simpler, ideal for regular languages, but they lack the memory capacity to handle nested structures or recursive patterns that PDAs manage effectively. While PDAs demonstrate strength in parsing programming languages and balanced parentheses, finite automata excel in fast lexical analysis with lower computational complexity.
Summary and Choosing the Right Model
Pushdown Automata (PDA) extend finite automata by incorporating a stack, enabling the recognition of context-free languages such as balanced parentheses and nested structures, which standard automata cannot process. Finite automata are sufficient for regular language recognition and offer simpler implementation and faster computation for tasks like lexical analysis. Choosing the right model depends on language complexity: PDAs are essential for parsing programming languages and context-free grammars, while finite automata work best for simpler pattern matching and tokenization.
Pushdown Automaton Infographic
 libterm.com
libterm.com