Central projection, also known as perspective projection, is a geometric transformation that maps three-dimensional objects onto a two-dimensional plane using lines that converge at a single point called the center of projection. This technique mimics how the human eye perceives depth and distance, making it essential in fields like computer graphics, technical drawing, and photography. Discover how understanding central projection can enhance your visualization skills by exploring the rest of this article.
Table of Comparison
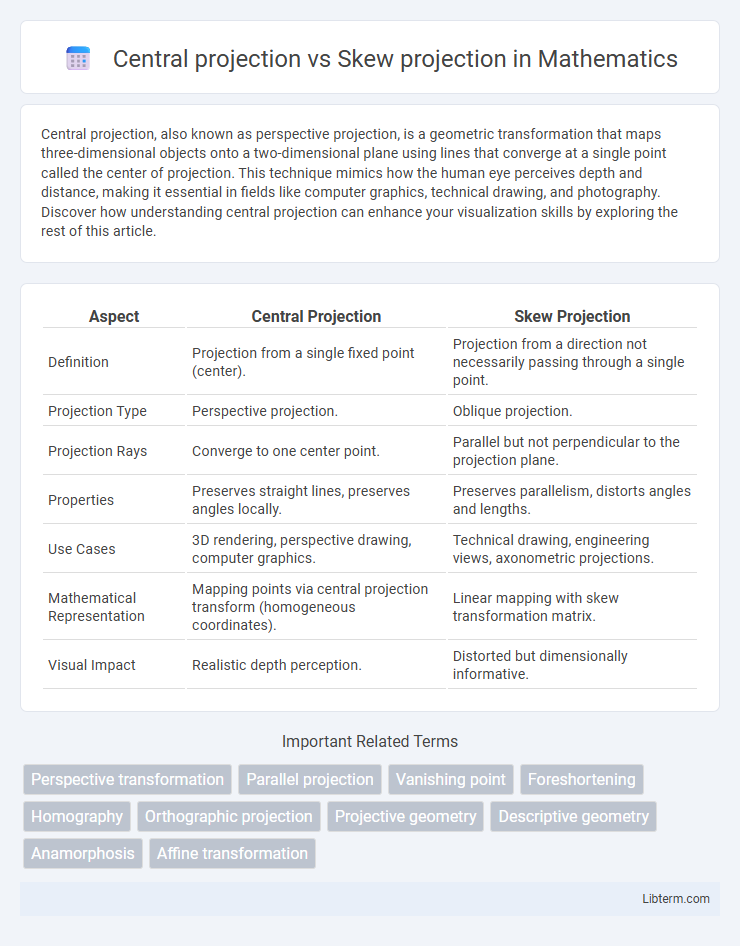
| Aspect | Central Projection | Skew Projection |
|---|---|---|
| Definition | Projection from a single fixed point (center). | Projection from a direction not necessarily passing through a single point. |
| Projection Type | Perspective projection. | Oblique projection. |
| Projection Rays | Converge to one center point. | Parallel but not perpendicular to the projection plane. |
| Properties | Preserves straight lines, preserves angles locally. | Preserves parallelism, distorts angles and lengths. |
| Use Cases | 3D rendering, perspective drawing, computer graphics. | Technical drawing, engineering views, axonometric projections. |
| Mathematical Representation | Mapping points via central projection transform (homogeneous coordinates). | Linear mapping with skew transformation matrix. |
| Visual Impact | Realistic depth perception. | Distorted but dimensionally informative. |
Introduction to Projection Methods in Graphics
Central projection, also known as perspective projection, simulates human eye perception by projecting 3D objects onto a 2D plane with lines converging at a single viewpoint, creating realistic depth and foreshortening effects. Skew projection, or oblique projection, shifts the projection plane parallel to the viewing direction without converging lines, maintaining parallelism and shape proportions but distorting spatial depth. Both projection methods are fundamental in computer graphics for rendering 3D models into 2D images, each optimized for different visualization requirements such as realism in central projection and technical accuracy in skew projection.
Understanding Central Projection
Central projection, also known as perspective projection, maps three-dimensional points onto a two-dimensional plane by projecting rays from a single viewpoint, creating images with realistic depth and scale. This method preserves the relative visual size of objects diminishing with distance, making it ideal for computer graphics and photography where depth perception is crucial. In contrast, skew projection distorts angles and lengths by projecting points along oblique directions, often used in technical drawings where parallelism rather than realism is emphasized.
Exploring Skew Projection
Skew projection is a type of parallel projection where the projection lines are not perpendicular to the projection plane, causing the image to be distorted but preserving parallelism. Unlike central projection, which maps points by lines converging at a single viewpoint and introduces perspective distortion, skew projection maintains consistent scale along certain directions, making it useful in technical drawing and engineering for representing objects without perspective foreshortening. Exploring skew projection enhances understanding of geometric transformations and aids in accurately visualizing structures where true dimensions need to be preserved in specific directions.
Key Differences Between Central and Skew Projection
Central projection, also known as perspective projection, maps 3D points onto a 2D plane by projecting lines through a single viewpoint, resulting in images with depth and realistic scale changes. Skew projection transforms objects by applying a shear factor, distorting shapes without preserving angles or lengths, commonly used in technical drawing to display objects without perspective convergence. Key differences include central projection's convergence of parallel lines towards vanishing points versus skew projection's parallel lines remaining parallel, and central projection's depth representation contrasted with skew projection's distortion for measurable projections.
Mathematical Principles of Central Projection
Central projection relies on the principle of projecting points from a 3D space onto a 2D plane via lines converging at a single viewpoint, defined mathematically by homogenous coordinates and perspective transformation matrices. The projection maps a point \( (X, Y, Z) \) in space to a point \( (x, y) \) on the image plane using the equations \( x = \frac{fX}{Z} \) and \( y = \frac{fY}{Z} \), where \( f \) represents the focal length. In contrast, skew projection involves non-uniform linear transformations without convergence, often represented by affine matrices lacking the division by depth parameter \( Z \).
Mathematical Principles of Skew Projection
Skew projection mathematically relies on transforming coordinates by projecting points onto a subspace along directions that are not perpendicular, defined by an oblique projection matrix with non-orthogonal eigenvectors. Unlike central projection, which maps points through a fixed center, skew projection involves linear transformations characterized by a projection operator \( P = A(A^TA)^{-1}A^T \) modified by a skewing matrix to control the angle and direction of projection. This principle enables the representation of figures in a distorted but geometrically consistent manner, essential for applications in computer graphics and geometric modeling where perspective effects differ from those of central projection.
Applications of Central Projection in Real-World Scenarios
Central projection is widely used in computer graphics for rendering 3D scenes onto 2D screens, providing realistic perspectives in video games and simulations. Architectural visualization relies on central projection to accurately depict spatial relationships and depth in building designs. In photography, central projection principles guide lens design to capture images with a natural field of view and perspective distortion.
Applications of Skew Projection in Various Fields
Skew projection finds critical applications in computer graphics for rendering scenes with oblique angles, enhancing visual depth without complex calculations. In engineering, it facilitates the design of mechanical parts by representing components from non-perpendicular viewpoints, aiding precise measurement. Architectural drafting benefits from skew projection by enabling the visualization of structures in unique perspectives, improving spatial understanding and design accuracy.
Advantages and Limitations of Each Projection Method
Central projection offers accurate perspective representation by converging lines toward a single vanishing point, making it ideal for realistic 3D visualization but can introduce distortion at the edges of the image. Skew projection allows for flexible, non-perpendicular projection angles, enabling easier representation of objects without distortion in certain views but lacks the realistic depth perception provided by central projection. Each method's suitability depends on the need for visual realism versus geometric simplicity in applications like computer graphics or technical drawing.
Choosing the Right Projection: Central vs Skew
Choosing the right projection depends on the desired visual effect and accuracy in representing three-dimensional objects. Central projection, also known as perspective projection, accurately mimics human vision by converging parallel lines at vanishing points, making it ideal for realistic depth representation in architectural and engineering drawings. Skew projection, a type of parallel projection with oblique angles, maintains true size and shape without convergence, making it suitable for technical illustrations where measurements must remain consistent.
Central projection Infographic
 libterm.com
libterm.com