Injective is a decentralized exchange protocol designed to enable fast, secure, and trustless trading of digital assets with zero gas fees and instant transaction finality. It leverages layer-2 scalability solutions and a decentralized order book to provide users with a seamless trading experience and access to various DeFi markets. Explore the full article to discover how Injective can transform your trading strategies and enhance your decentralized finance experience.
Table of Comparison
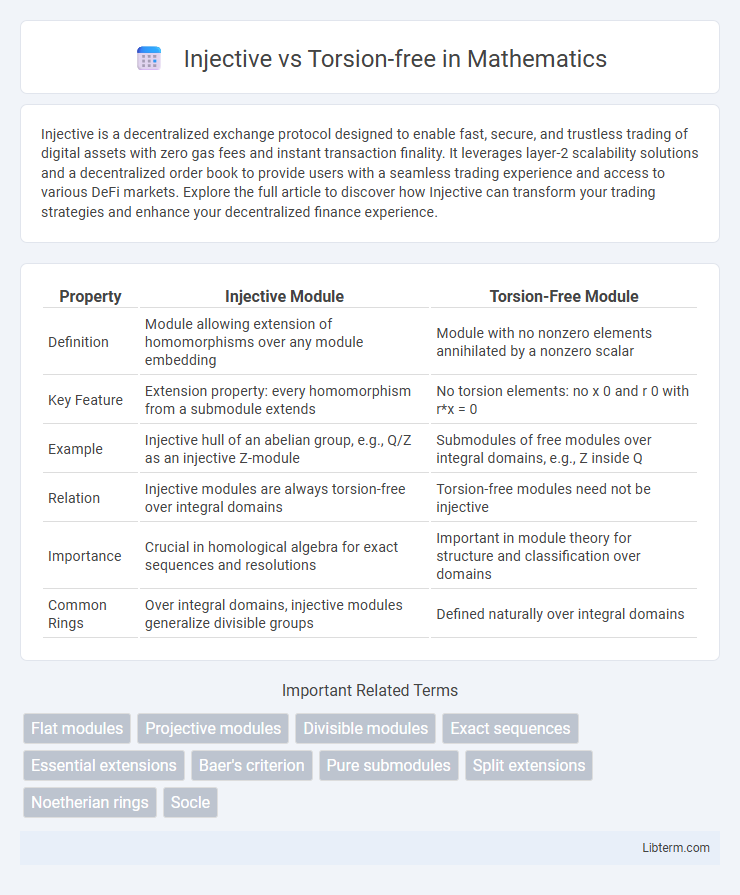
| Property | Injective Module | Torsion-Free Module |
|---|---|---|
| Definition | Module allowing extension of homomorphisms over any module embedding | Module with no nonzero elements annihilated by a nonzero scalar |
| Key Feature | Extension property: every homomorphism from a submodule extends | No torsion elements: no x 0 and r 0 with r*x = 0 |
| Example | Injective hull of an abelian group, e.g., Q/Z as an injective Z-module | Submodules of free modules over integral domains, e.g., Z inside Q |
| Relation | Injective modules are always torsion-free over integral domains | Torsion-free modules need not be injective |
| Importance | Crucial in homological algebra for exact sequences and resolutions | Important in module theory for structure and classification over domains |
| Common Rings | Over integral domains, injective modules generalize divisible groups | Defined naturally over integral domains |
Introduction to Injective and Torsion-Free Structures
Injective modules are characterized by their ability to extend homomorphisms from submodules to the entire module, ensuring that every exact sequence ending with the injective module splits. Torsion-free structures maintain non-zero elements free from annihilation by non-zero scalars, preserving integrity under scalar multiplication within integral domains. Understanding these properties is essential in module theory, as injective modules provide a form of maximal extensibility while torsion-free modules exhibit stability and embed naturally into their field of fractions.
Defining Injective Modules: Core Concepts
Injective modules are defined by their ability to extend module homomorphisms from submodules to the entire module, characterizing them as essential in homological algebra. This property ensures that any exact sequence involving an injective module remains exact after applying the Hom functor, highlighting their role in the study of module extensions. In contrast, torsion-free modules are primarily defined by the absence of elements annihilated by nonzero scalars, emphasizing different structural aspects than injectivity.
Understanding Torsion-Free Modules: Key Properties
Torsion-free modules are characterized by having no nonzero elements annihilated by nonzero scalars, ensuring that multiplication by any nonzero element of the ring remains injective. This property implies a strong structural rigidity, making torsion-free modules particularly important in the study of integral domains and their module theory. Understanding torsion-free modules involves analyzing their behavior under tensor products and homomorphisms, revealing critical distinctions from injective modules, which are defined by their ability to extend homomorphisms from submodules.
Fundamental Differences Between Injective and Torsion-Free
Injective modules are characterized by their ability to absorb homomorphisms from submodules, ensuring extension properties that lead to direct summands in any module containing them. Torsion-free modules, on the other hand, are defined by the absence of elements annihilated by nonzero scalars, which guarantees no torsion elements but does not imply any extension property. The fundamental difference lies in injectivity being a categorical property related to module homomorphism extensions, whereas torsion-freeness is an algebraic property concerning element annihilation.
Examples of Injective Modules in Algebra
Injective modules play a critical role in module theory by allowing every exact sequence to split, which is not generally true for torsion-free modules. Examples of injective modules include the divisible abelian groups such as the rational numbers \(\mathbb{Q}\) considered as a module over the integers \(\mathbb{Z}\), and the module of all p-adic integers used in commutative algebra. Unlike torsion-free modules that only avoid elements annihilated by nonzero scalars, injective modules ensure extensibility of homomorphisms, making them essential in homological algebra and representation theory.
Real-World Applications of Torsion-Free Modules
Torsion-free modules play a crucial role in algebraic geometry and number theory, enabling the classification of vector bundles and simplifying the structure of abelian groups without elements of finite order. These modules are fundamental in coding theory, where their torsion-free property ensures error detection and correction in data transmission over noisy channels. Injective modules, by contrast, are primarily used to extend modules and solve homological problems, but torsion-free modules offer more direct applications in modeling real-world systems with stability and consistency constraints.
Conditions for a Module to Be Both Injective and Torsion-Free
A module is both injective and torsion-free when it is an injective module over an integral domain that does not contain any nonzero elements annihilated by nonzero elements of the ring. Over a principal ideal domain (PID), an injective torsion-free module is necessarily a divisible module, which is a direct sum of copies of the field of fractions. This characterization links injectivity to divisibility, ensuring the module can be embedded into an injective hull while maintaining torsion-free properties.
Injective vs Torsion-Free: Implications in Module Theory
Injective modules exhibit a property of extending homomorphisms, making them essential in solving module-theoretic extension problems, while torsion-free modules lack elements annihilated by nonzero scalars, ensuring injectivity does not imply torsion-freeness. In module theory, injective modules provide a framework for understanding exact sequences and homological dimensions, whereas torsion-free modules are critical in examining modules over integral domains, especially in the context of divisibility and localization. The distinction shapes the study of module decomposition, with injective modules often serving as building blocks in decompositions, contrasting the structural constraints imposed by torsion-free conditions.
Comparative Analysis: Strengths and Limitations
Injective modules exhibit the strength of being direct summands of their extensions, ensuring a highly flexible and well-behaved homological structure, crucial for simplifying exact sequences in module theory, while torsion-free modules excel in maintaining the absence of elements annihilated by nonzero scalars, preserving the purity of algebraic structures like integral domains. Injectivity guarantees the existence of module homomorphisms extension from submodules, making them indispensable in homological algebra, whereas torsion-free modules are vital in number theory and algebraic geometry for maintaining integral properties and avoiding zero divisors. Despite their robustness, injective modules can be complex and less constructive in explicit classifications, while torsion-free modules, though structurally simpler, lack the universal extension property that injective modules provide.
Conclusion: Choosing Between Injective and Torsion-Free Structures
Choosing between injective and torsion-free structures depends on the specific algebraic context and desired properties; injective modules ensure extensibility and exactness preservation, making them ideal for homological algebra applications. Torsion-free structures, characterized by the absence of elements annihilated by nonzero scalars, provide a foundation for maintaining integral properties and simpler submodule behavior. Prioritizing injective modules is advantageous for advanced module-theoretic constructions, while torsion-free modules suit scenarios emphasizing structural rigidity and kernel-free behavior.
Injective Infographic
 libterm.com
libterm.com