Negative semidefinite matrices have all their eigenvalues less than or equal to zero, ensuring that the quadratic form associated with the matrix is always non-positive. These matrices play a crucial role in optimization problems, stability analysis, and control theory, where they help characterize concavity and system behavior. Dive deeper into this article to explore the properties, applications, and examples of negative semidefinite matrices to enhance Your understanding.
Table of Comparison
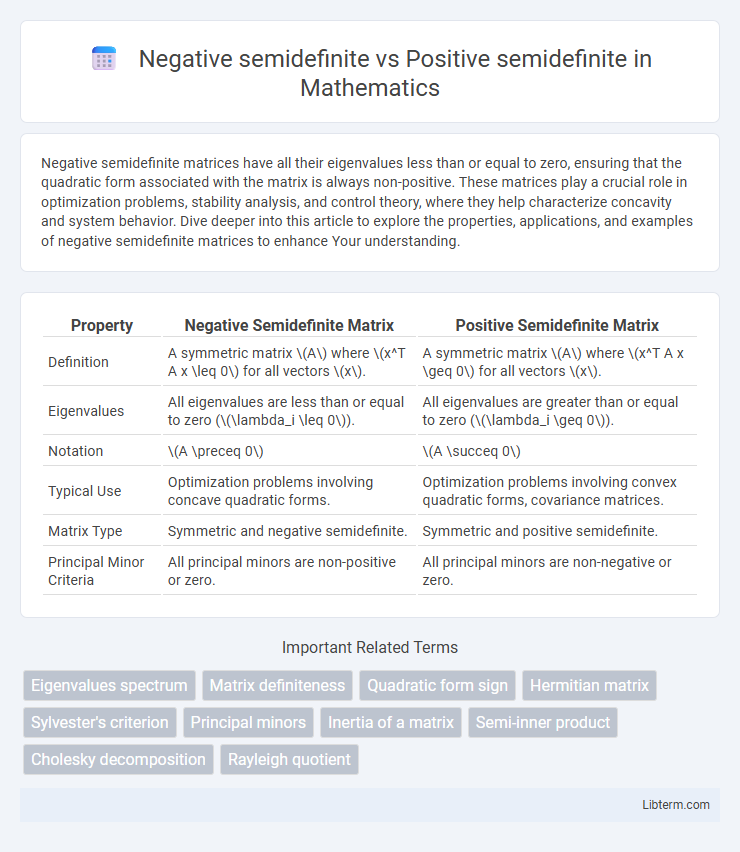
| Property | Negative Semidefinite Matrix | Positive Semidefinite Matrix |
|---|---|---|
| Definition | A symmetric matrix \(A\) where \(x^T A x \leq 0\) for all vectors \(x\). | A symmetric matrix \(A\) where \(x^T A x \geq 0\) for all vectors \(x\). |
| Eigenvalues | All eigenvalues are less than or equal to zero (\(\lambda_i \leq 0\)). | All eigenvalues are greater than or equal to zero (\(\lambda_i \geq 0\)). |
| Notation | \(A \preceq 0\) | \(A \succeq 0\) |
| Typical Use | Optimization problems involving concave quadratic forms. | Optimization problems involving convex quadratic forms, covariance matrices. |
| Matrix Type | Symmetric and negative semidefinite. | Symmetric and positive semidefinite. |
| Principal Minor Criteria | All principal minors are non-positive or zero. | All principal minors are non-negative or zero. |
Introduction to Semidefinite Matrices
Semidefinite matrices are symmetric matrices characterized by their eigenvalues, where positive semidefinite matrices have all non-negative eigenvalues, ensuring xTAx >= 0 for any vector x. Negative semidefinite matrices, conversely, have all non-positive eigenvalues, satisfying xTAx <= 0 for any vector x. These properties are fundamental in optimization, control theory, and quadratic forms, distinguishing how matrices influence convexity and stability in mathematical models.
Defining Positive Semidefinite Matrices
Positive semidefinite matrices are square matrices whose eigenvalues are all non-negative, ensuring that for any non-zero vector \(x\), the quadratic form \(x^T A x \geq 0\). Negative semidefinite matrices, conversely, have non-positive eigenvalues, resulting in \(x^T A x \leq 0\) for any vector \(x\). This distinction plays a critical role in optimization problems, numerical analysis, and stability assessments in control theory.
Understanding Negative Semidefinite Matrices
Negative semidefinite matrices are symmetric matrices whose eigenvalues are all less than or equal to zero, indicating that for any nonzero vector x, the quadratic form xTAx is less than or equal to zero. These matrices play a crucial role in optimization and stability analysis, as they describe concave functions and systems that dissipate energy or contract. Understanding the distinction from positive semidefinite matrices, which have nonnegative eigenvalues and correspond to convex functions, is essential for applications in control theory, economics, and machine learning.
Key Mathematical Properties
Negative semidefinite matrices have all eigenvalues less than or equal to zero, ensuring that for any vector x, the quadratic form xTAx is less than or equal to zero. Positive semidefinite matrices have all eigenvalues greater than or equal to zero, guaranteeing non-negative quadratic forms xTAx for all vectors x. Both types exhibit symmetric properties and play crucial roles in optimization, stability analysis, and covariance matrices in statistics.
Eigenvalues: The Core Distinction
Negative semidefinite matrices have eigenvalues that are all less than or equal to zero, indicating that their quadratic forms never produce positive outputs. Positive semidefinite matrices possess eigenvalues that are all greater than or equal to zero, ensuring nonnegative quadratic forms. This difference in eigenvalue sign is the fundamental criterion separating negative semidefinite matrices from positive semidefinite matrices.
Criteria for Identification
Positive semidefinite matrices have all non-negative eigenvalues, ensuring that for any vector x, the quadratic form xTAx is greater than or equal to zero. Negative semidefinite matrices exhibit non-positive eigenvalues, so the quadratic form xTAx is less than or equal to zero for all vectors x. The identification criteria rely on eigenvalue analysis or checking that all leading principal minors have non-negative signs for positive semidefiniteness, and non-positive signs for negative semidefiniteness.
Applications in Optimization
Positive semidefinite matrices play a crucial role in convex optimization problems, ensuring that quadratic forms are convex and enabling efficient algorithm convergence. Negative semidefinite matrices are often used to characterize concave functions, important for maximizing objectives in concave optimization frameworks. Both matrix types are fundamental in semidefinite programming, where matrix constraints define feasible regions for optimization tasks in control theory, signal processing, and machine learning.
Practical Examples and Use Cases
Negative semidefinite matrices frequently appear in optimization problems involving concave functions, such as in economics for utility maximization under risk constraints. Positive semidefinite matrices are essential in machine learning for covariance matrices, kernel methods, and ensuring convexity in quadratic programming. Control theory uses positive semidefinite matrices to guarantee system stability through Lyapunov functions, while negative semidefinite matrices help analyze energy dissipation in dynamic systems.
Common Misconceptions
Negative semidefinite matrices are often mistakenly thought to be the simple opposites of positive semidefinite matrices, but their key difference lies in the nonpositive versus nonnegative eigenvalues, not just sign inversion. A frequent misconception is that any matrix with all nonpositive diagonal entries is negative semidefinite; in reality, the eigenvalue spectrum, not solely diagonal terms, determines definiteness. Another common error confuses negative semidefinite matrices with negative definite ones, overlooking the allowance for zero eigenvalues in semidefinite cases that affect matrix behavior in optimization and stability analysis.
Summary: Choosing the Right Matrix Type
Negative semidefinite matrices have all eigenvalues less than or equal to zero, often representing concave quadratic forms, while positive semidefinite matrices have eigenvalues greater than or equal to zero, representing convex forms. Selecting the appropriate matrix type depends on the problem context, such as stability analysis favoring negative semidefinite matrices and optimization constraints relying on positive semidefinite matrices. Correct identification ensures accurate modeling in applications like control theory, machine learning, and structural engineering.
Negative semidefinite Infographic
 libterm.com
libterm.com