Intrametric technology enhances precision and efficiency by enabling seamless communication within a single metric system. It optimizes data integration and simplifies complex workflows, ensuring consistent and accurate results. Discover how intrametric solutions can transform your processes by reading the full article.
Table of Comparison
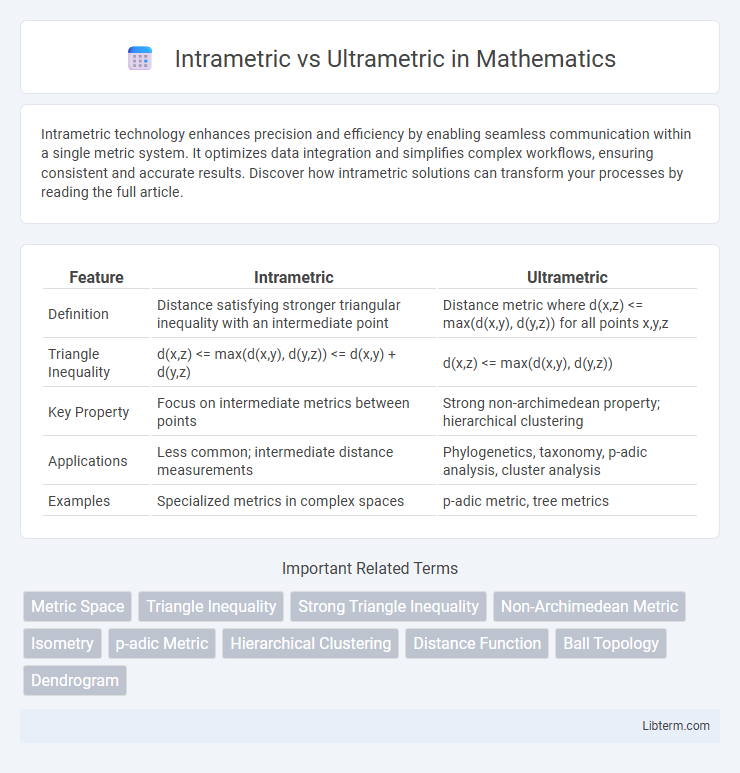
| Feature | Intrametric | Ultrametric |
|---|---|---|
| Definition | Distance satisfying stronger triangular inequality with an intermediate point | Distance metric where d(x,z) <= max(d(x,y), d(y,z)) for all points x,y,z |
| Triangle Inequality | d(x,z) <= max(d(x,y), d(y,z)) <= d(x,y) + d(y,z) | d(x,z) <= max(d(x,y), d(y,z)) |
| Key Property | Focus on intermediate metrics between points | Strong non-archimedean property; hierarchical clustering |
| Applications | Less common; intermediate distance measurements | Phylogenetics, taxonomy, p-adic analysis, cluster analysis |
| Examples | Specialized metrics in complex spaces | p-adic metric, tree metrics |
Introduction to Metric Spaces
Metric spaces provide a framework to measure distances between points, where intrametric and ultrametric spaces represent specialized types with distinct distance properties. An intrametric space satisfies the usual metric axioms but emphasizes strong triangle inequalities, while an ultrametric space strengthens this by ensuring the ultrametric inequality, where the distance between any two points is at most the maximum of the distances between each point and a third point. Ultrametric spaces often arise in p-adic number theory and hierarchical clustering, offering unique geometric insights within the broader context of metric space theory.
Defining Intrametric and Ultrametric Distances
Intrametric distances satisfy the inequality d(x,z) <= max{d(x,y), d(y,z)} for any points x, y, z, indicating that the distance between two points cannot exceed the larger of the two distances passing through a third point, blending properties of metric and ultrametric spaces. Ultrametric distances strengthen this condition by requiring d(x,z) <= max{d(x,y), d(y,z)} with the added ultrametric inequality that the triangle formed is isosceles with the base no longer than the equal sides, characteristic of hierarchical clustering structures. These definitions establish distinct geometric constraints that influence data interpretation in clustering and taxonomy, with ultrametrics enforcing a stricter tree-like metric than intrametrics.
Mathematical Properties of Intrametrics
Intrametrics satisfy a relaxed version of the ultrametric inequality, where the distance between points is bounded by the maximum of pairwise distances but with less strict constraints. Unlike ultrametrics, intrametrics do not require the strong triangle inequality to hold for all triples, leading to greater flexibility in modeling hierarchical structures. Intrametrics maintain non-negativity, symmetry, and identity of indiscernibles, making them useful in areas such as clustering and phylogenetics where partial hierarchical relationships exist.
Ultrametric Inequality Explained
Ultrametric inequality states that for any three points x, y, and z in a metric space, the distance d(x, z) is at most the maximum of d(x, y) and d(y, z), strengthening the standard triangle inequality used in intrametric spaces. This property implies that every triangle in an ultrametric space is either isosceles with the two longer sides equal or equilateral, creating tight hierarchical clustering structures. Ultrametrics are essential in fields like phylogenetics and p-adic number theory due to their ability to model nested or tree-like relationships efficiently.
Key Differences between Intrametric and Ultrametric
Intrametric distances measure the direct dissimilarity between points without strict hierarchical constraints, whereas ultrametric distances impose a stronger triangle inequality, ensuring that for any three points, the two larger distances are equal. Ultrametric spaces naturally represent hierarchical clustering and tree-like structures because all triplets satisfy the ultrametric inequality, while intrametric distances do not necessarily reflect hierarchical relationships. Key differences include the application scope, where ultrametrics are essential in phylogenetics and taxonomy, and intrametrics provide a more general framework for measuring similarities in metric spaces.
Real-World Applications of Intrametric Metrics
Intrametric metrics are widely used in clustering algorithms for hierarchical data analysis, enabling efficient grouping in fields like bioinformatics and psychology where similarity relationships are non-linear. Unlike ultrametric metrics, which require strict triangle inequalities facilitating tree-like structures, intrametrics allow for more flexible data representations crucial in natural language processing and pattern recognition. Real-world applications include taxonomic classification, speech and image recognition, and network analysis where capturing nuanced proximities improves accuracy and interpretability.
Ultrametric Spaces in Phylogenetics and Taxonomy
Ultrametric spaces, characterized by a strengthened triangle inequality where the distance between any two points is at most the maximum of the distances to a third point, are fundamental in phylogenetics and taxonomy for representing evolutionary relationships. These spaces enable the construction of rooted phylogenetic trees where all leaves are equidistant from the root, reflecting consistent molecular clock assumptions and divergence times among species. Ultrametric distances facilitate clustering algorithms like UPGMA, providing a framework for inferring taxonomic hierarchies based on genetic or phenotypic similarity measures.
Visualizing Intrametric vs Ultrametric Spaces
Visualizing intrametric spaces involves representing data points where the triangle inequality is strengthened so that the maximum distance dominates, typically displayed using rooted trees or dendrograms highlighting hierarchical clustering with equal distances within clusters. Ultrametric spaces emphasize strict hierarchical relationships where all triangles are isosceles with the base no longer than the equal sides, often visualized through ultrametric trees that reveal clear, nested cluster structures and uniform branching levels. These visual tools differentiate intrametric spaces by their relaxed ultrametric inequality and ultrametric spaces by their precise, strict hierarchy, supporting clearer interpretation of underlying metric properties in data analysis.
Common Misconceptions and Pitfalls
Intrametric and ultrametric distances differ fundamentally in their triangle inequality constraints, where ultrametric distances satisfy the strong triangle inequality d(x,z) <= max{d(x,y), d(y,z)} used in hierarchical clustering and intrametric distances relax this condition. A common misconception is treating intrametrics as a subset of ultrametrics, while intrametrics allow more flexibility and do not always produce strict equidistant clusters. Pitfalls include misapplying ultrametric assumptions to datasets better suited for intrametric models, leading to inaccurate hierarchical representations and clustering results.
Future Directions in Metric Space Research
Future directions in metric space research emphasize exploring the distinctions and applications of intrametric and ultrametric spaces in data analysis and machine learning. Advancements aim to enhance clustering algorithms and hierarchical modeling by leveraging the strong triangle inequality characteristic of ultrametric spaces, improving robustness and interpretability. Developing scalable computational methods for intrametric structures will further enable the analysis of high-dimensional and complex datasets across bioinformatics, taxonomy, and network science.
Intrametric Infographic
 libterm.com
libterm.com