Simplicial complexes are mathematical structures made up of points, line segments, triangles, and higher-dimensional analogs that are used to study topological spaces. They provide a framework for analyzing shapes and data in fields such as algebraic topology, computational geometry, and data analysis. Discover how simplicial complexes can deepen your understanding of complex geometric and topological problems by exploring the rest of this article.
Table of Comparison
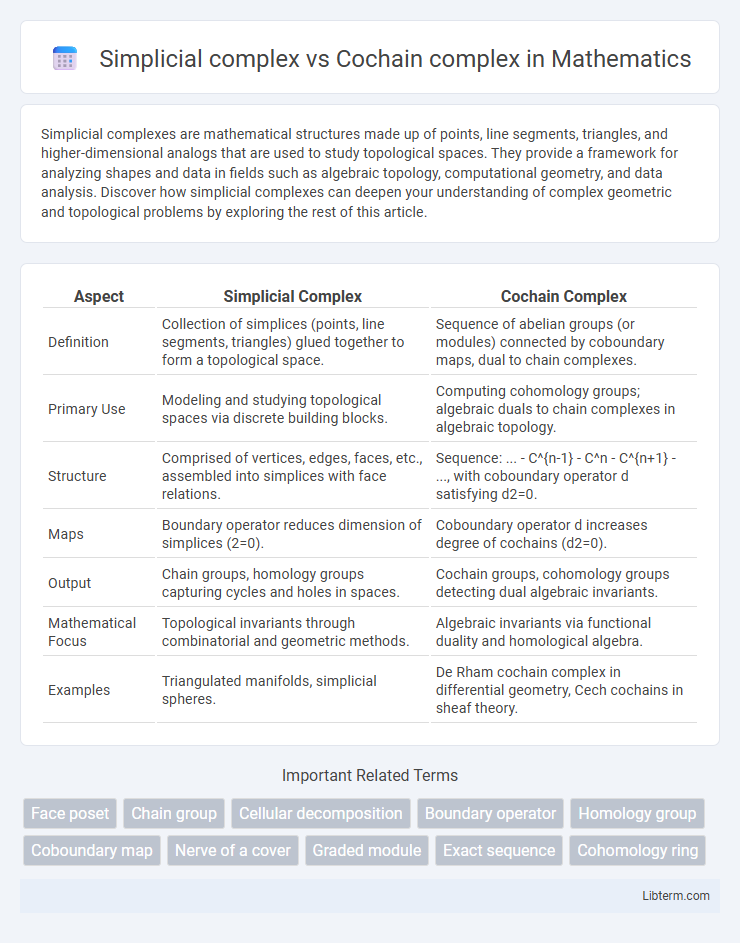
| Aspect | Simplicial Complex | Cochain Complex |
|---|---|---|
| Definition | Collection of simplices (points, line segments, triangles) glued together to form a topological space. | Sequence of abelian groups (or modules) connected by coboundary maps, dual to chain complexes. |
| Primary Use | Modeling and studying topological spaces via discrete building blocks. | Computing cohomology groups; algebraic duals to chain complexes in algebraic topology. |
| Structure | Comprised of vertices, edges, faces, etc., assembled into simplices with face relations. | Sequence: ... - C^{n-1} - C^n - C^{n+1} - ..., with coboundary operator d satisfying d2=0. |
| Maps | Boundary operator reduces dimension of simplices (2=0). | Coboundary operator d increases degree of cochains (d2=0). |
| Output | Chain groups, homology groups capturing cycles and holes in spaces. | Cochain groups, cohomology groups detecting dual algebraic invariants. |
| Mathematical Focus | Topological invariants through combinatorial and geometric methods. | Algebraic invariants via functional duality and homological algebra. |
| Examples | Triangulated manifolds, simplicial spheres. | De Rham cochain complex in differential geometry, Cech cochains in sheaf theory. |
Introduction to Simplicial Complexes
Simplicial complexes provide a combinatorial framework for studying topological spaces by decomposing them into simplices such as vertices, edges, and higher-dimensional triangles. Unlike cochain complexes, which involve algebraic operations on cochains and focus on differential structures, simplicial complexes emphasize the geometric and combinatorial assembly of simplices. This structure enables the computation of topological invariants like homology groups by analyzing the connectivity and arrangement of simplices.
Understanding Cochain Complexes
Cochain complexes consist of sequences of abelian groups or modules connected by coboundary maps, where each map's composition with the next is zero, facilitating the computation of cohomology groups. These structures generalize simplicial cohomology by associating algebraic data with simplices, enabling detailed analysis of topological spaces. Understanding cochain complexes is essential for exploring dualities in algebraic topology and for applications in homological algebra.
Key Definitions and Terminology
A simplicial complex is a collection of simplices (vertices, edges, triangles, and higher-dimensional analogs) that are glued together in a combinatorial way satisfying specific intersection properties, while a cochain complex consists of a sequence of abelian groups or modules connected by coboundary maps. In a simplicial complex, the key objects include simplices and faces, whereas the cochain complex involves cochains, coboundary operators, and cohomology groups. The cochain complex often arises from a simplicial complex by assigning algebraic data to each simplex dimension, enabling computations of topological invariants.
Structure and Construction of Simplicial Complexes
Simplicial complexes consist of simplices such as points, line segments, and triangles assembled to form a topological space, organized by their face relations and dimension. Their construction involves defining a finite set of vertices and specifying which subsets form simplices, ensuring closure under taking faces. In contrast, cochain complexes arise algebraically from these simplicial complexes by associating cochains--functions on simplices--and defining coboundary operators to study topological invariants via cohomology.
Algebraic Framework of Cochain Complexes
Cochain complexes provide an algebraic framework through a sequence of abelian groups or modules connected by coboundary maps, enabling the computation of cohomology. Unlike simplicial complexes that rely on combinatorial structures of simplices, cochain complexes abstract these relationships algebraically, focusing on functions or cochains defined on the simplices. This algebraic viewpoint facilitates the study of topological invariants by transforming geometric problems into homological algebra.
Comparison: Homology vs Cohomology
Simplicial complexes provide a geometric framework for computing homology groups, which measure topological features like holes and connected components through chains and boundary operators. In contrast, cochain complexes use cochains and coboundary operators to define cohomology groups, capturing dual algebraic invariants such as cocycles and coboundaries that offer insights into topological spaces' functions and structures. Homology emphasizes cycles and boundaries, while cohomology focuses on cocycles and coboundaries, often enabling richer algebraic structures like cup products and duality theorems.
Applications in Topology and Algebra
Simplicial complexes provide a combinatorial framework for studying topological spaces through simplices, enabling the computation of homology groups that classify spaces based on their holes and voids. Cochain complexes, arising from algebraic structures on these simplicial complexes, facilitate the calculation of cohomology groups, which reveal richer algebraic invariants such as cup products essential in algebraic topology. In algebra, cochain complexes are pivotal in examining extensions, deformations, and obstructions within modules and chain complexes, bridging topology and homological algebra through their applications in spectral sequences and derived functors.
Similarities Between Simplicial and Cochain Complexes
Simplicial complexes and cochain complexes both provide algebraic structures used in algebraic topology to study topological spaces. They consist of graded sets or modules connected by boundary or coboundary operators that satisfy nilpotency conditions, enabling the computation of homology and cohomology groups. Both frameworks facilitate the analysis of shape and connectivity by translating geometric information into algebraic invariants.
Differences: Computational and Theoretical Aspects
Simplicial complexes are combinatorial structures used to study topological spaces through simplices, enabling computational topology methods like persistent homology, while cochain complexes involve algebraic constructions with cochains and coboundary operators, facilitating the calculation of cohomology groups. Computationally, simplicial complexes provide a geometric framework that is often more intuitive for algorithms handling high-dimensional data, whereas cochain complexes emphasize algebraic operations that may require more abstract algebraic manipulation. Theoretically, simplicial complexes focus on building space from simple pieces and understanding connectivity, whereas cochain complexes offer a dual perspective useful in deriving invariants like cup products and cohomological operations.
Conclusion: Choosing the Right Complex
Selecting between a simplicial complex and a cochain complex depends on the specific topological or algebraic problem and the desired computational approach. Simplicial complexes provide a direct combinatorial representation of topological spaces, ideal for geometric intuition and homology computations. Cochain complexes, on the other hand, facilitate algebraic manipulations and cohomology theories, offering greater flexibility for duality principles and functional analysis in algebraic topology.
Simplicial complex Infographic
 libterm.com
libterm.com