Poisson algebra combines the structures of associative and Lie algebras, providing a framework for studying Hamiltonian mechanics and various geometric contexts. It features a commutative product and a Lie bracket that satisfies the Leibniz rule, enabling the modeling of both algebraic and differential properties. Discover how Poisson algebras influence mathematical physics and geometry throughout the rest of this article.
Table of Comparison
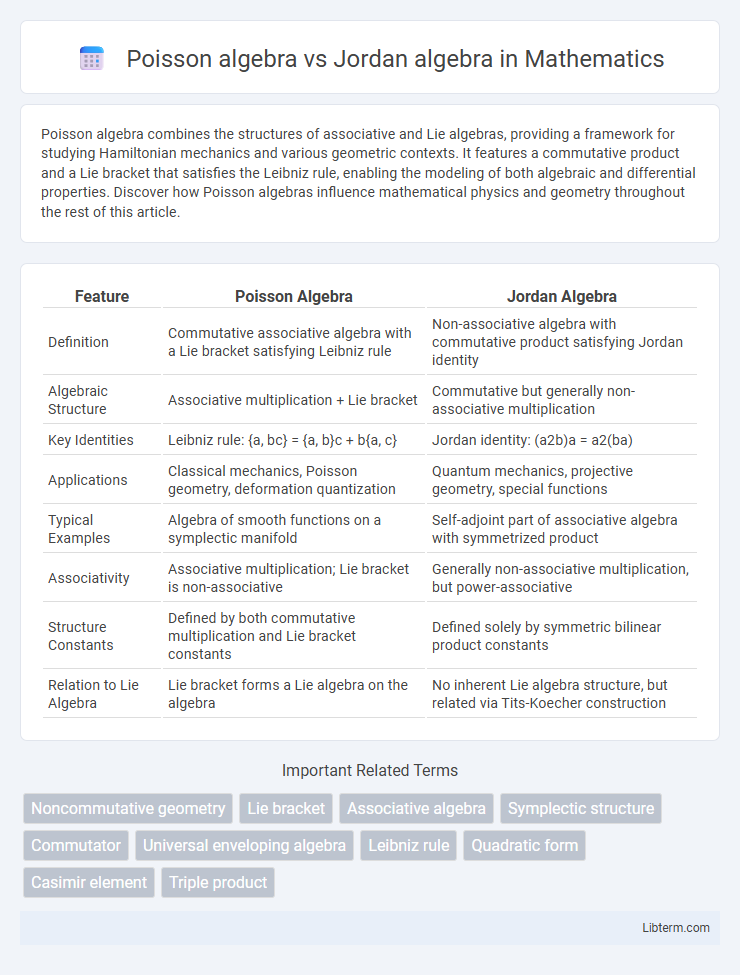
| Feature | Poisson Algebra | Jordan Algebra |
|---|---|---|
| Definition | Commutative associative algebra with a Lie bracket satisfying Leibniz rule | Non-associative algebra with commutative product satisfying Jordan identity |
| Algebraic Structure | Associative multiplication + Lie bracket | Commutative but generally non-associative multiplication |
| Key Identities | Leibniz rule: {a, bc} = {a, b}c + b{a, c} | Jordan identity: (a2b)a = a2(ba) |
| Applications | Classical mechanics, Poisson geometry, deformation quantization | Quantum mechanics, projective geometry, special functions |
| Typical Examples | Algebra of smooth functions on a symplectic manifold | Self-adjoint part of associative algebra with symmetrized product |
| Associativity | Associative multiplication; Lie bracket is non-associative | Generally non-associative multiplication, but power-associative |
| Structure Constants | Defined by both commutative multiplication and Lie bracket constants | Defined solely by symmetric bilinear product constants |
| Relation to Lie Algebra | Lie bracket forms a Lie algebra on the algebra | No inherent Lie algebra structure, but related via Tits-Koecher construction |
Introduction to Poisson and Jordan Algebras
Poisson algebras combine a commutative associative algebra with a Lie bracket satisfying the Leibniz rule, modeling classical mechanics' phase space structures. Jordan algebras are non-associative algebras defined by the Jordan identity, originally developed to formalize observables in quantum mechanics. Both algebraic structures play crucial roles in mathematical physics, with Poisson algebras emphasizing classical Poisson brackets and Jordan algebras focusing on symmetric products and quantum observables.
Historical Background and Mathematical Origins
Poisson algebras originated from the study of classical mechanics in the 19th century, formalizing the algebraic structure of observables with a Lie bracket and associative product that satisfy the Leibniz rule, reflecting the properties of the Poisson bracket on smooth functions. Jordan algebras emerged in the 1930s from Pascual Jordan's work in quantum mechanics, aiming to generalize the algebraic structure of observables by focusing on commutative but nonassociative products, inspired by the symmetrized product of operators in Hilbert spaces. The development of both algebras marked significant advancements in linking algebraic frameworks with physical theories, influencing areas such as symplectic geometry for Poisson algebras and quantum theory for Jordan algebras.
Defining Poisson Algebra: Structure and Examples
Poisson algebra is a mathematical structure combining a commutative associative algebra with a Lie bracket satisfying the Leibniz rule, enabling the construction of Hamiltonian mechanics in algebraic terms. It features a bilinear Poisson bracket {*,*} that is antisymmetric, satisfies the Jacobi identity, and acts as a derivation with respect to the associative multiplication, exemplified in the algebra of smooth functions on a symplectic manifold. Contrastingly, Jordan algebras are commutative but non-associative algebras defined by the Jordan identity, primarily used in quantum mechanics without a Lie bracket structure.
Defining Jordan Algebra: Structure and Applications
Jordan algebra is a non-associative algebra defined by the commutative product satisfying the Jordan identity (x2*y)*x = x2*(y*x), primarily used to model observables in quantum mechanics and optimize algebraic structures in differential geometry. Unlike Poisson algebras, which combine Lie and associative algebra structures to handle Hamiltonian dynamics, Jordan algebras emphasize commutativity and the quadratic representation, critical for studying projective geometry and operator algebras. Their applications span quantum theory, statistical mechanics, and the theory of exceptional Lie groups, showcasing their unique role in abstract algebra and mathematical physics.
Core Axioms: Comparing Fundamental Properties
Poisson algebras combine a commutative associative product with a Lie bracket satisfying the Leibniz rule, integrating both associative and Lie algebra structures in their core axioms. Jordan algebras feature a commutative, but generally non-associative product obeying the Jordan identity, which emphasizes symmetrized multiplication without a Lie bracket. The key distinction in fundamental properties lies in Poisson algebras enforcing the Lie bracket's derivation condition on the associative product, while Jordan algebras focus solely on non-associative commutative multiplication satisfying the Jordan polynomial identity.
Key Differences in Algebraic Operations
Poisson algebras combine a commutative associative product with a Lie bracket satisfying the Leibniz rule, enabling the modeling of both associative and Lie algebraic structures simultaneously. Jordan algebras, in contrast, are non-associative algebras defined by a commutative product satisfying the Jordan identity, emphasizing symmetrized product operations without a Lie bracket. The key difference lies in the presence of the Lie bracket in Poisson algebras, which influences the algebraic operations by intertwining associative and Lie structures, whereas Jordan algebras focus solely on commutative, non-associative multiplication adhering to specific polynomial identities.
Roles in Mathematical Physics and Quantum Theory
Poisson algebras serve as a fundamental structure in classical mechanics, encoding the phase space with a Lie bracket that governs the dynamics of observables and enabling the transition to quantum theory via deformation quantization. Jordan algebras, on the other hand, provide a non-associative algebraic framework modeling observables in quantum mechanics, particularly emphasizing the algebraic properties of self-adjoint operators in Hilbert spaces. Both algebras facilitate the formulation of physical theories: Poisson algebras underpin the classical-quantum correspondence, while Jordan algebras capture the algebraic essence of quantum observables beyond associative operator algebras.
Representation Theory: Poisson vs Jordan Algebras
Poisson algebra representation theory explores modules equipped with both associative and Lie algebraic actions that satisfy the Leibniz rule, emphasizing the dual nature of commutative and Lie structures in deformation quantization. Jordan algebra representation theory focuses on modules preserving the commutative, non-associative product governed by the Jordan identity, with important applications in projective geometry and quantum mechanics. The key distinction lies in Poisson representations managing a Lie-Poisson bracket alongside commutative multiplication, while Jordan representations maintain compatibility with the symmetric Jordan product, influencing their respective module categories and morphisms.
Interconnections and Hybrid Structures
Poisson algebras combine associative and Lie algebra structures with a compatible bracket operation, serving as a fundamental framework in classical mechanics and deformation quantization. Jordan algebras emphasize commutative but generally non-associative multiplication, often appearing in quantum theory and projective geometry. Hybrid structures, such as Poisson-Jordan algebras, explore the interplay between Lie-related bracket operations and Jordan-type products, revealing rich interconnections that enable advancements in non-associative geometry and integrable systems.
Future Directions: Research and Applications
Future research in Poisson algebras centers on their role in mathematical physics, particularly in deformation quantization and integrable systems, where exploring noncommutative deformations can reveal new quantum structures. Jordan algebras find promising applications in quantum information theory and symmetric spaces, with ongoing studies aimed at understanding their automorphism groups and extension to infinite dimensions. Interdisciplinary approaches integrating Poisson and Jordan algebraic frameworks may unlock novel insights in non-associative geometry and theoretical physics models.
Poisson algebra Infographic
 libterm.com
libterm.com