Linear order refers to arranging items, events, or elements sequentially from beginning to end based on a specific criterion such as time, size, or importance. Understanding linear order is essential for organizing information clearly, enhancing comprehension, and improving problem-solving efficiency. Explore the rest of the article to discover how mastering linear order can benefit your daily tasks and analytical skills.
Table of Comparison
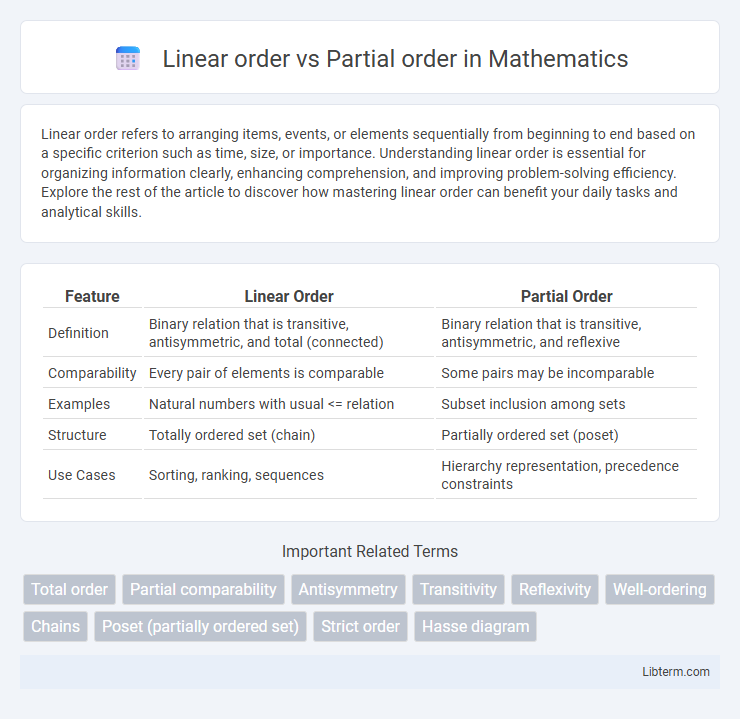
| Feature | Linear Order | Partial Order |
|---|---|---|
| Definition | Binary relation that is transitive, antisymmetric, and total (connected) | Binary relation that is transitive, antisymmetric, and reflexive |
| Comparability | Every pair of elements is comparable | Some pairs may be incomparable |
| Examples | Natural numbers with usual <= relation | Subset inclusion among sets |
| Structure | Totally ordered set (chain) | Partially ordered set (poset) |
| Use Cases | Sorting, ranking, sequences | Hierarchy representation, precedence constraints |
Introduction to Order Relations
Order relations categorize elements based on their arrangement or precedence, with linear orders requiring every pair of elements to be comparable, forming a strict or total sequence. Partial orders allow some elements to remain incomparable, reflecting hierarchy or dependency structures without enforcing a complete sequence. These order relations underpin key concepts in mathematics, computer science, and data organization by defining how elements relate within sets.
Defining Linear Order
Linear order is a type of ordering relation where every pair of elements is comparable, meaning for any two elements a and b, either a <= b or b <= a holds true. This strict comparability ensures a total or linear sequence without ambiguity in element ranking. Unlike partial order, which allows some elements to be incomparable, linear order provides a complete and transitive hierarchy essential in sorting algorithms and ordered data structures.
Understanding Partial Order
Partial order defines a binary relation over a set that is reflexive, antisymmetric, and transitive, allowing some elements to be incomparable, unlike linear order which requires every pair to be comparable. Understanding partial order is essential in fields like computer science and mathematics for modeling hierarchies, dependency structures, and scheduling problems where not all elements have a sequential relationship. Partial orders enable the representation of complex systems where elements can coexist without strict precedence, facilitating flexible and realistic data organization.
Key Differences Between Linear and Partial Order
Linear order is a type of partial order where every pair of elements is comparable, meaning for any two elements a and b, either a <= b or b <= a holds true. Partial order, by contrast, allows elements to be incomparable, providing a broader structure defined by reflexivity, antisymmetry, and transitivity but not total comparability. The key difference lies in the comparability condition: linear orders enforce total comparability, while partial orders permit incomparability among elements.
Examples of Linear Order in Mathematics
A linear order, also known as a total order, arranges elements so every pair is comparable, such as the natural numbers with the usual less than or equal relation (<=). Examples include the standard ordering of real numbers, integers, and rational numbers, where each pair satisfies comparability, antisymmetry, and transitivity. Unlike partial orders where some elements may be incomparable, linear orders provide a complete sequencing of elements, critical in algorithms and sorting processes.
Real-World Applications of Partial Order
Partial orders model real-world scenarios where elements have a hierarchical or dependency relationship without requiring every pair to be comparable, such as task scheduling in project management where some tasks must precede others without a strict sequence for all tasks. They are essential in database theory for representing data dependencies and version control systems that track changes across branches in software development. Partial orders also underpin preference rankings and decision-making processes where options may be incomparable but still partially ordered based on certain criteria.
Properties of Linear Order
Linear orders exhibit totality, antisymmetry, and transitivity, meaning every pair of elements is comparable, no two distinct elements precede each other, and the order relation is consistent across elements. Unlike partial orders, linear orders ensure a complete ordering without incomparability, allowing sequences to be arranged in a single, uninterrupted progression. These properties make linear orders crucial in scheduling, sorting algorithms, and any application requiring a definitive sequence of elements.
Properties of Partial Order
Partial order is characterized by three key properties: reflexivity, antisymmetry, and transitivity, which distinguish it from linear order. Reflexivity ensures every element is comparable to itself, antisymmetry prevents distinct elements from being mutually comparable in both directions, and transitivity maintains consistent ordering across elements. Unlike linear order, partial order does not require comparability for all pairs, allowing some elements to remain unordered relative to each other.
Comparing Visualization: Hasse Diagrams and Chains
Hasse diagrams visualize partial orders by representing elements as nodes connected through edges that imply order without showing all transitive relations, allowing clear interpretation of dependencies and hierarchy in complex sets. In contrast, linear orders appear as chains in Hasse diagrams, where every element is comparable, resulting in a simple, unbranched path that emphasizes total comparability. The difference in visualization highlights the flexibility of partial orders for representing non-linear relationships versus the strict sequential nature of linear orders.
Choosing Between Linear and Partial Order in Problem Solving
Choosing between linear order and partial order in problem solving depends on the problem's complexity and constraints. Linear orders require all elements to be comparable, making them suitable for totally ordered tasks like scheduling with strict precedence, whereas partial orders allow incomparability, ideal for representing hierarchical or dependency structures with unrelated elements. Selecting partial order can optimize flexibility and efficiency when some tasks or elements do not have a strict sequential relationship, enabling parallel processing or concurrent execution.
Linear order Infographic
 libterm.com
libterm.com