An infinite set is a collection of elements that has no end, meaning its size cannot be counted or matched with any finite number. This concept plays a crucial role in various branches of mathematics, including calculus and set theory, where understanding the properties of infinite sets helps explore the nature of numbers and functions. Discover how infinite sets impact mathematical thinking and why they are fundamental to your comprehension of advanced math topics in the rest of this article.
Table of Comparison
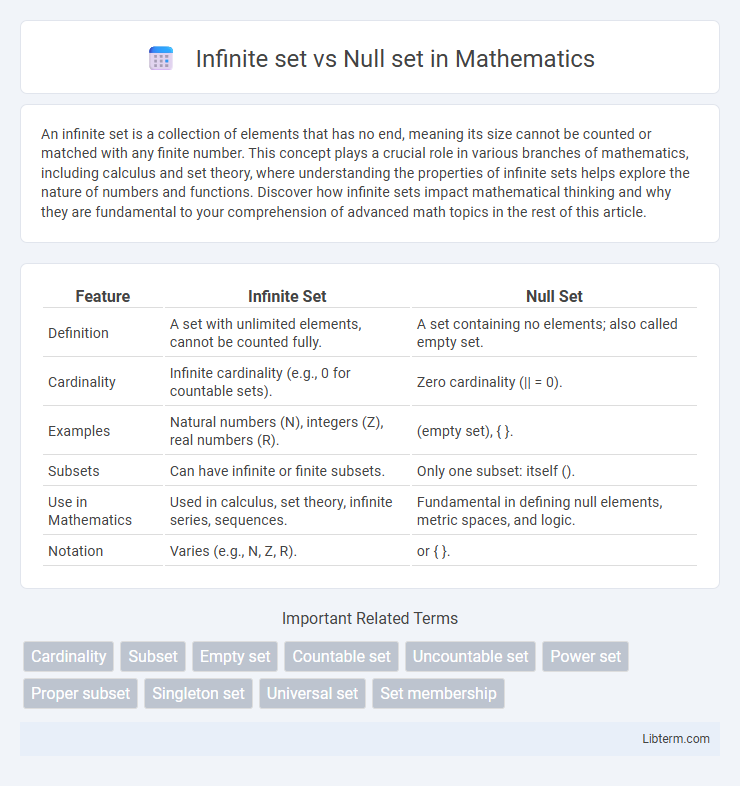
| Feature | Infinite Set | Null Set |
|---|---|---|
| Definition | A set with unlimited elements, cannot be counted fully. | A set containing no elements; also called empty set. |
| Cardinality | Infinite cardinality (e.g., 0 for countable sets). | Zero cardinality (|| = 0). |
| Examples | Natural numbers (N), integers (Z), real numbers (R). | (empty set), { }. |
| Subsets | Can have infinite or finite subsets. | Only one subset: itself (). |
| Use in Mathematics | Used in calculus, set theory, infinite series, sequences. | Fundamental in defining null elements, metric spaces, and logic. |
| Notation | Varies (e.g., N, Z, R). | or { }. |
Introduction to Sets in Mathematics
In mathematics, an infinite set contains infinitely many elements, such as the set of natural numbers, whereas a null set, also called an empty set, contains no elements at all. Infinite sets are fundamental in set theory and are characterized by their non-finite cardinality, while null sets serve as the identity element for union operations. Understanding the distinction between infinite and null sets is crucial for grasping more advanced concepts in mathematics, including cardinality and set operations.
Defining Infinite Sets
Infinite sets are collections of elements with no finite limit, characterized by the ability to establish one-to-one correspondences with proper subsets, such as the set of natural numbers. Unlike null sets, which contain no elements, infinite sets demonstrate unbounded cardinality, often explored through concepts like countability and uncountability. Defining infinite sets involves understanding their properties related to size, structure, and the principles of infinite cardinalities in set theory.
Understanding the Null Set
The null set, also known as the empty set, contains no elements and is a fundamental concept in set theory, representing the idea of 'nothingness' within a set framework. Unlike an infinite set, which has unlimited elements and can be enumerated or described through infinite sequences or cardinalities such as Aleph-null (0), the null set has a fixed cardinality of zero. Understanding the null set is essential for grasping concepts of subsets, intersections, and set operations, as it serves as the unique subset of every set, including infinite ones.
Key Differences: Infinite Set vs Null Set
An infinite set contains an unlimited number of elements, such as the set of natural numbers, whereas a null set, also known as an empty set, contains no elements at all. The cardinality of an infinite set is unbounded or infinite, while the cardinality of a null set is zero. Infinite sets allow for operations involving infinite sequences and limits, but null sets represent the absence of any elements, making them fundamental in set theory as the unique empty subset of all sets.
Examples of Infinite Sets
Examples of infinite sets include the set of natural numbers {1, 2, 3, ...}, the set of integers {..., -2, -1, 0, 1, 2, ...}, and the set of real numbers between 0 and 1. These sets contain infinitely many elements, unlike the null set, which has no elements at all. Infinite sets are fundamental in mathematics for studying sequences, series, and continuous functions.
Examples of Null Sets
Null sets, also known as empty sets, contain no elements, exemplified by the solution set of the equation x^2 + 1 = 0 over real numbers. In contrast, infinite sets like the set of natural numbers have an unbounded number of elements. The null set is symbolized by and is a fundamental concept in set theory representing the absence of elements.
Applications of Infinite and Null Sets
Infinite sets are fundamental in calculus and computer science, enabling modeling of continuous data and algorithmic complexities involving unbounded elements. Null sets, crucial in measure theory and probability, help identify events or conditions with zero impact or probability, aiding in refined mathematical analysis and statistical interpretation. Both concepts underpin advanced fields like topology, functional analysis, and stochastic processes, facilitating rigorous theoretical development and practical problem-solving.
Set Notation and Representation
An infinite set is represented in set notation as {x | x U, P(x)} where U is the universal set and P(x) is a property satisfied by infinitely many elements, such as the set of natural numbers N = {1, 2, 3, ...}. The null set, denoted by or {}, contains no elements and is defined as {x | x U, False}, meaning no x satisfies the condition. Infinite sets can be described using ellipses or set-builder notation to capture their unbounded nature, while the null set's empty representation signifies the absence of any elements.
Common Misconceptions
Infinite sets are often mistakenly believed to be uncountably large, but many infinite sets, such as the set of natural numbers, are countably infinite. A common misconception about the null set is that it contains elements such as zero or null itself, while in reality, it is completely empty with no elements at all. Understanding these distinctions clarifies fundamental concepts in set theory and avoids confusion in mathematical reasoning.
Summary and Conclusion
Infinite sets contain an uncountable or countably endless number of elements, exemplified by natural numbers or real numbers. Null sets, also known as empty sets, contain no elements and serve as the foundational concept of zero cardinality in set theory. Understanding the distinction between infinite and null sets is crucial for advanced mathematics, as it underpins theories in calculus, probability, and logic.
Infinite set Infographic
 libterm.com
libterm.com