Real estate investment offers long-term financial growth and portfolio diversification with tangible asset value. Market trends, property location, and economic factors significantly impact investment returns and risks. Explore this article to uncover essential tips for maximizing your real estate investment success.
Table of Comparison
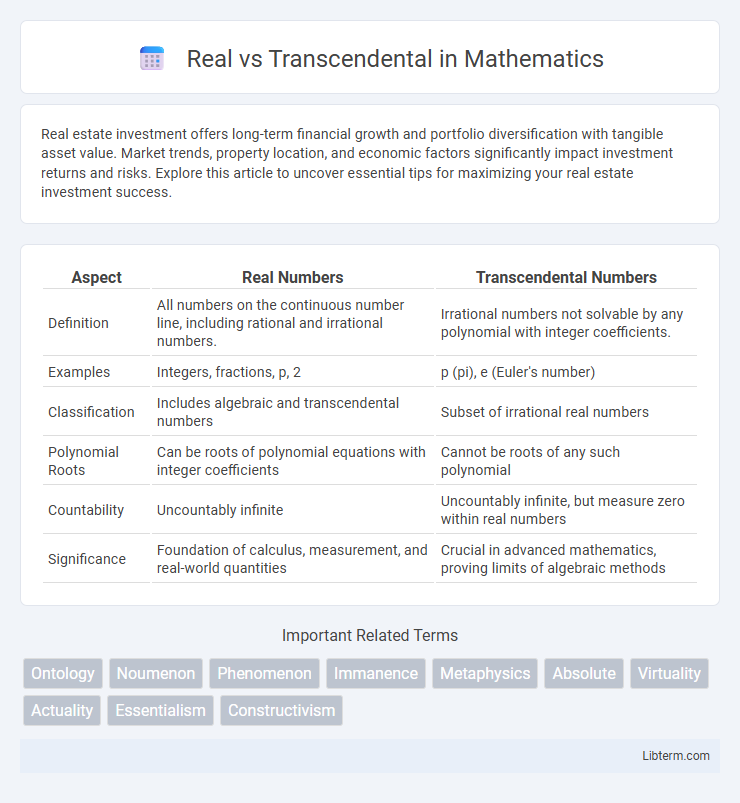
| Aspect | Real Numbers | Transcendental Numbers |
|---|---|---|
| Definition | All numbers on the continuous number line, including rational and irrational numbers. | Irrational numbers not solvable by any polynomial with integer coefficients. |
| Examples | Integers, fractions, p, 2 | p (pi), e (Euler's number) |
| Classification | Includes algebraic and transcendental numbers | Subset of irrational real numbers |
| Polynomial Roots | Can be roots of polynomial equations with integer coefficients | Cannot be roots of any such polynomial |
| Countability | Uncountably infinite | Uncountably infinite, but measure zero within real numbers |
| Significance | Foundation of calculus, measurement, and real-world quantities | Crucial in advanced mathematics, proving limits of algebraic methods |
Understanding Real Numbers: Foundations and Properties
Real numbers encompass all rational and irrational numbers, forming a continuous number line essential for measuring quantities and distances. Their foundational properties include closure, commutativity, associativity, distributivity, identity elements, and inverses, supporting arithmetic and calculus operations. Transcendental numbers, a subset of real numbers like p and e, are non-algebraic and cannot be roots of any non-zero polynomial with rational coefficients, highlighting the complex hierarchy within the real number system.
Defining Transcendental Numbers: Beyond Algebraic Limits
Transcendental numbers are defined as real or complex numbers that are not roots of any non-zero polynomial equation with rational coefficients, distinguishing them from algebraic numbers. These numbers, such as p and e, extend beyond the algebraic limits by defying solutions to polynomial equations, showcasing properties that cannot be captured by algebraic expressions. The study of transcendental numbers highlights their significance in number theory and mathematical analysis, revealing deeper structural complexities in the continuum of real numbers.
Historical Milestones: Discovery of Real and Transcendental Numbers
The distinction between real and transcendental numbers was established through key historical milestones such as the proof of the irrationality of 2 by the ancient Greeks and Euler's work on the transcendence of e. The formal discovery of transcendental numbers was solidified by Charles Hermite in 1873 when he proved that e is transcendental, followed by Ferdinand von Lindemann's 1882 demonstration of the transcendence of p. These breakthroughs marked critical developments in number theory, expanding the understanding of the real number line by identifying numbers that cannot be roots of any polynomial with rational coefficients.
Key Differences: Real Numbers vs Transcendental Numbers
Real numbers include all rational and irrational numbers that can be represented on the number line, encompassing integers, fractions, and non-repeating decimals. Transcendental numbers are a subset of irrational numbers that are not roots of any non-zero polynomial equation with rational coefficients, such as p and e. The key difference lies in algebraic properties: real numbers may satisfy polynomial equations, while transcendental numbers cannot be expressed as solutions to such equations.
Famous Examples: From π and e to Rational Numbers
Famous examples of real numbers include rational numbers like 1/2 and integers such as -3, while transcendental numbers consist of non-algebraic figures like p and e, known for their infinite, non-repeating decimal expansions. The number p (pi) represents the ratio of a circle's circumference to its diameter, fundamental in geometry and trigonometry, whereas e (Euler's number) is the base of natural logarithms essential in calculus and exponential growth models. Rational numbers can be exactly expressed as fractions, contrasting with transcendental numbers, which cannot be roots of any non-zero polynomial equation with rational coefficients.
Role in Mathematics: Real and Transcendental Number Applications
Real numbers form the foundation of calculus, algebra, and real analysis, enabling measurements, modeling, and solving equations across various scientific fields. Transcendental numbers, such as p and e, play a crucial role in complex analysis, number theory, and the proof of limits and approximations that cannot be achieved using algebraic numbers alone. Their unique properties support advanced mathematical concepts, including transcendence proofs and the characterization of irrational quantities in computations and cryptography.
Theories and Proofs: Establishing Transcendence
Theories on transcendental numbers focus on proving that such numbers are not roots of any non-zero polynomial equation with rational coefficients, distinguishing them from algebraic numbers. Classical proofs, such as Hermite's proof of the transcendence of e and Lindemann's extension showing p is transcendental, rely on sophisticated analytical techniques including exponential function properties and linear independence over the rationals. Modern transcendence theory builds on these foundations through advances in Diophantine approximation and transcendence measures, establishing rigorous criteria to confirm the transcendental nature of numbers beyond classical examples.
Algebraic vs Transcendental: Classification and Criteria
Algebraic numbers are roots of non-zero polynomial equations with rational coefficients, while transcendental numbers cannot be expressed as solutions to any such polynomial. The classification relies on determining whether a complex number satisfies an algebraic equation or not, where criteria involve polynomial degree and coefficient rationality. Transcendental numbers, such as pi and e, fundamentally differ from algebraic numbers by their inability to be approximated through finite algebraic relations.
Challenges in Identifying Transcendental Numbers
Identifying transcendental numbers poses significant challenges due to their non-algebraic nature, as they cannot be expressed as roots of any polynomial equation with rational coefficients. Unlike algebraic numbers, which are countable and can be systematically cataloged, transcendental numbers form an uncountably infinite set, making explicit examples rare and difficult to prove. Key transcendental numbers such as p and e required advanced techniques in number theory and analysis, highlighting the complexity in distinguishing transcendental numbers from real algebraic counterparts.
Future Insights: Implications for Mathematics and Science
Transcendental numbers, such as p and e, extend beyond real algebraic numbers, challenging traditional mathematical frameworks and inspiring new computational models. Future research aims to harness these numbers for advancements in cryptography, quantum computing, and complex system analysis. Understanding the distribution and properties of transcendental numbers will deepen insights into fundamental mathematical constants and their applications in theoretical physics.
Real Infographic
 libterm.com
libterm.com