A cyclic group is an algebraic structure consisting of elements generated by repeatedly applying a group operation to a single element called the generator. These groups are fundamental in abstract algebra due to their simple structure and wide applications in number theory, cryptography, and symmetry analysis. Explore the rest of the article to deepen your understanding of cyclic groups and their critical role in mathematics.
Table of Comparison
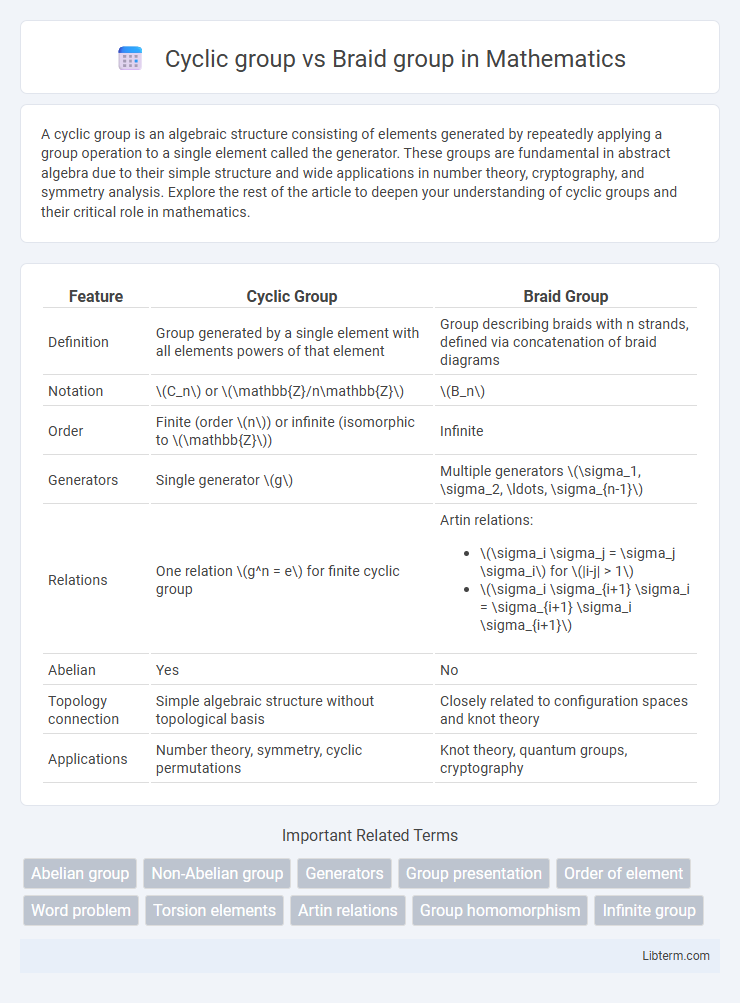
| Feature | Cyclic Group | Braid Group |
|---|---|---|
| Definition | Group generated by a single element with all elements powers of that element | Group describing braids with n strands, defined via concatenation of braid diagrams |
| Notation | \(C_n\) or \(\mathbb{Z}/n\mathbb{Z}\) | \(B_n\) |
| Order | Finite (order \(n\)) or infinite (isomorphic to \(\mathbb{Z}\)) | Infinite |
| Generators | Single generator \(g\) | Multiple generators \(\sigma_1, \sigma_2, \ldots, \sigma_{n-1}\) |
| Relations | One relation \(g^n = e\) for finite cyclic group | Artin relations:
|
| Abelian | Yes | No |
| Topology connection | Simple algebraic structure without topological basis | Closely related to configuration spaces and knot theory |
| Applications | Number theory, symmetry, cyclic permutations | Knot theory, quantum groups, cryptography |
Introduction to Cyclic Groups and Braid Groups
Cyclic groups are algebraic structures generated by a single element, where every group element can be expressed as successive powers of this generator; they are fundamental in group theory and often denoted as \( \mathbb{Z}/n\mathbb{Z} \) for finite cases or \( \mathbb{Z} \) for infinite cyclic groups. Braid groups, denoted by \( B_n \), consist of \( n \)-strand braids with group operations defined by concatenation, representing complex non-commutative structures with rich topological and algebraic properties, often used in knot theory and cryptography. While cyclic groups are Abelian and structurally simple, braid groups exhibit non-Abelian characteristics with generators satisfying specific braid relations, highlighting fundamental differences in their algebraic behavior and applications.
Fundamental Definitions
A cyclic group is an algebraic structure generated by a single element whose powers produce all elements in the group, characterized by being abelian and finite or infinite depending on the order of the generator. In contrast, a braid group consists of equivalence classes of braids with n strands under composition, defined by Artin's presentation with generators s_i subject to specific braid relations reflecting the non-commutative nature. Fundamental differences lie in cyclic groups having a simple, linear structure with one generator, while braid groups exhibit complex non-abelian structure arising from intertwining strands and topological properties.
Algebraic Structure Comparison
Cyclic groups are algebraic structures generated by a single element where every element is a power of this generator, characterized by a simple commutative property and a finite or infinite order. In contrast, braid groups consist of complex generators representing strand crossings with non-commutative relations governed by braid relations, reflecting their topological nature. The fundamental difference lies in cyclic groups' abelian property versus braid groups' non-abelian structure, resulting in a richer algebraic framework in braid groups.
Generators and Relations
Cyclic groups are generated by a single element with the defining relation that this element raised to the group's order equals the identity, represented as \( \langle g \mid g^n = e \rangle \). Braid groups, however, have multiple generators \( \sigma_1, \sigma_2, \ldots, \sigma_{n-1} \) with relations reflecting braid interactions, including the Artin relations: \( \sigma_i \sigma_j = \sigma_j \sigma_i \) for \( |i-j| > 1 \) and \( \sigma_i \sigma_{i+1} \sigma_i = \sigma_{i+1} \sigma_i \sigma_{i+1} \). Unlike cyclic groups, braid groups are infinite, non-abelian, and have complex algebraic structures crucial to topology and group theory.
Visual Representations
Cyclic groups are visually represented as points arranged evenly around a circle, highlighting their rotational symmetry and repetitive structure through simple, uniform diagrams. Braid groups are depicted using strands interlacing in complex patterns, illustrating their intricate intertwining and the non-commutative nature of their generators. These visual distinctions emphasize the fundamental differences in algebraic properties and topological interpretations between cyclic and braid groups.
Applications in Mathematics
Cyclic groups, characterized by their simple structure generated by a single element, are fundamental in number theory and cryptography, facilitating tasks like modular arithmetic and group-based encryption algorithms. Braid groups, with their complex non-abelian structure, play a crucial role in topology and knot theory, providing algebraic invariants essential for understanding the entanglement of strands and contributing to quantum computing through anyon models. Both groups serve as pivotal tools in abstract algebra, yet their distinct properties enable diverse applications across mathematical disciplines, including symmetric structures for cyclic groups and mapping class groups for braid groups.
Role in Cryptography
Cyclic groups provide a simple algebraic structure with efficient computational properties widely used in classical cryptographic protocols such as Diffie-Hellman key exchange and RSA. Braid groups offer a non-commutative complexity that forms the foundation of emerging cryptographic schemes, leveraging hard problems like the conjugacy search problem to enhance security against quantum attacks. The contrasting algebraic complexity of braid groups compared to cyclic groups positions them as promising candidates for post-quantum cryptography frameworks.
Key Differences and Similarities
Cyclic groups are abelian groups generated by a single element with elements forming a finite or infinite sequence under the group operation, while braid groups consist of multiple strands with non-commutative generators satisfying braid relations. Both groups are fundamental in algebra and topology, exhibiting structure through generators and relations, but cyclic groups have simpler, commutative properties compared to the more complex, non-commutative braid groups. Braid groups play a significant role in knot theory and quantum computing, whereas cyclic groups underpin basic group theory concepts and appear in modular arithmetic.
Examples and Illustrations
A cyclic group is the simplest example of a group generated by a single element, such as the integers modulo n under addition, denoted by \( \mathbb{Z}_n \), where every element is a power of a generator \( g \). In contrast, a braid group \( B_n \) consists of n strands that can be interlaced with generators \( \sigma_i \) representing crossings between adjacent strands, where relations encode the braid moves; for example, \( B_3 \) has generators \( \sigma_1 \) and \( \sigma_2 \) satisfying \( \sigma_1 \sigma_2 \sigma_1 = \sigma_2 \sigma_1 \sigma_2 \). Illustrations often depict a cyclic group as points arranged in a circle representing successive powers of a generator, while braid groups are shown as sets of intertwined strings highlighting non-commutative actions and topological entanglements.
Conclusion: Choosing the Right Group
Choosing the right group depends on the specific algebraic properties and applications required. Cyclic groups offer simplicity and ease of computation, making them ideal for problems involving periodicity and rotational symmetry. Braid groups, with their complex structure and rich topological interpretations, are better suited for advanced applications in knot theory, cryptography, and mathematical physics.
Cyclic group Infographic
 libterm.com
libterm.com