Cellular resolution refers to the capacity to distinguish individual cells within a biological tissue during imaging or analysis, essential for accurate diagnosis and research. Advanced microscopy techniques and imaging technologies have dramatically improved cellular resolution, enabling detailed observation of cellular structures and functions. Explore the rest of the article to understand how cellular resolution advancements impact biomedical studies and clinical applications.
Table of Comparison
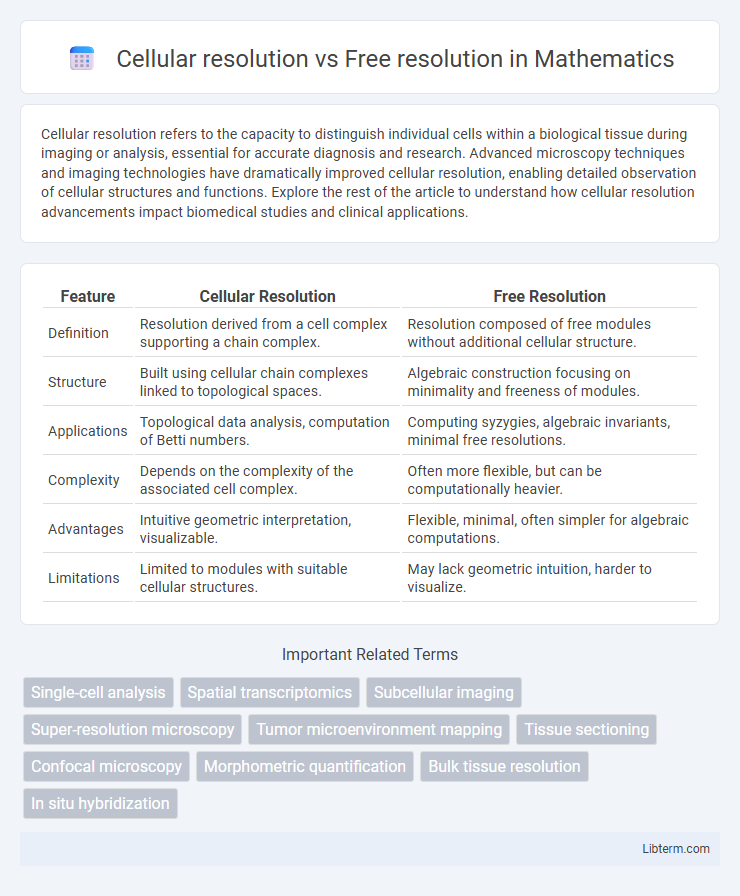
| Feature | Cellular Resolution | Free Resolution |
|---|---|---|
| Definition | Resolution derived from a cell complex supporting a chain complex. | Resolution composed of free modules without additional cellular structure. |
| Structure | Built using cellular chain complexes linked to topological spaces. | Algebraic construction focusing on minimality and freeness of modules. |
| Applications | Topological data analysis, computation of Betti numbers. | Computing syzygies, algebraic invariants, minimal free resolutions. |
| Complexity | Depends on the complexity of the associated cell complex. | Often more flexible, but can be computationally heavier. |
| Advantages | Intuitive geometric interpretation, visualizable. | Flexible, minimal, often simpler for algebraic computations. |
| Limitations | Limited to modules with suitable cellular structures. | May lack geometric intuition, harder to visualize. |
Understanding Cellular Resolution: A Definition
Cellular resolution refers to the ability to distinguish individual cells within a biological sample, enabling detailed analysis at the single-cell level. This precise resolution is crucial for identifying cellular heterogeneity and understanding complex tissue architecture. In contrast, free resolution lacks this specificity, often aggregating signals from multiple cells, which limits the potential for detailed cellular insights.
What is Free Resolution? An Overview
Free resolution refers to the maximum achievable detail in imaging or microscopy without the constraints imposed by cellular boundaries or structures. It allows for the visualization and analysis of features at a molecular or subcellular level, enabling high precision in spatial measurement and data interpretation. Free resolution is critical in contexts requiring accurate mapping of biomolecules independent of cellular compartmentalization, enhancing the understanding of biological processes.
Key Differences Between Cellular and Free Resolution
Cellular resolution refers to the precise segmentation of individual cells within a biological sample, enabling detailed analysis of cellular morphology and function, whereas free resolution pertains to image resolution without specific cellular boundaries, often used in broader tissue or organ imaging. Cellular resolution typically requires advanced imaging techniques such as confocal microscopy or single-cell RNA sequencing to achieve high specificity at the single-cell level. Free resolution allows for general structural visualization but lacks the granularity needed for cell-specific data extraction, making it less suitable for studies demanding cellular heterogeneity insights.
Importance of Resolutions in Algebraic Topology
Cellular resolution and free resolution are crucial in algebraic topology for understanding the structure of modules over a ring through chain complexes. Cellular resolutions derive from cell complexes and provide a geometrically intuitive way to decompose spaces, aiding in the computation of homological invariants. Free resolutions, as projective chain complexes with free modules, offer algebraic tools to analyze module properties, making the choice between them essential for efficient calculations in topological and algebraic contexts.
Applications of Cellular Resolution in Commutative Algebra
Cellular resolution is a powerful tool in commutative algebra for constructing minimal free resolutions of monomial ideals, using cell complexes that reflect the combinatorial structure of the ideals. This approach enables precise computation of Betti numbers and syzygies, facilitating the study of algebraic invariants such as projective dimension and regularity. Cellular resolutions have applications in algebraic geometry, combinatorics, and topological data analysis by providing explicit connections between algebraic properties and underlying geometric or combinatorial objects.
Advantages and Limitations of Free Resolution
Free resolution offers significant advantages in microscopy by providing unrestricted spatial resolution that adapts dynamically to the sample's optical properties, allowing detailed observation of complex biological structures at the nanoscale. Its limitations include increased susceptibility to noise and optical aberrations, requiring advanced computational algorithms for accurate image reconstruction, which can be resource-intensive. Unlike cellular resolution, which is constrained to fixed spatial scales, free resolution enables more flexible imaging but demands greater expertise and equipment investment to achieve optimal results.
How to Construct Cellular Resolutions
Cellular resolutions are constructed by associating monomial ideals with cell complexes, translating algebraic information into topological structures that reflect minimal free resolutions. The process involves labeling cells with monomials and ensuring the differential maps correspond to boundary maps of the complex, yielding a free resolution supported on the cell complex. This method contrasts with free resolutions, which are purely algebraic and may lack such combinatorial or geometric interpretations, facilitating insights into syzygies via cellular topology.
When to Use Cellular vs Free Resolution
Cellular resolution is ideal for chronic wound management and small, localized tissue repairs where targeted cellular analysis enhances treatment precision; free resolution suits acute trauma or large surface wounds requiring expansive tissue regeneration without intricate cellular targeting. Use cellular resolution when detailed cellular interactions and tissue microenvironment assessments are critical for personalized therapy decisions, while free resolution is preferred for rapid coverage and repair of widespread tissue damage. Selecting cellular resolution optimizes outcomes in regenerative medicine by enabling focused interventions, whereas free resolution prioritizes efficient healing in broadly affected wound sites.
Recent Developments in Resolution Techniques
Recent developments in resolution techniques have highlighted the distinction between cellular resolution and free resolution in imaging technologies, particularly in microscopy and medical diagnostics. Cellular resolution focuses on achieving detailed visualization at the individual cell level, essential for studying cellular functions and pathologies, while free resolution emphasizes flexible imaging scales adaptable to various specimen sizes without sacrificing clarity. Innovations such as super-resolution microscopy and adaptive optics have significantly enhanced cellular resolution, enabling researchers to observe subcellular structures with unprecedented precision, whereas advancements in computational imaging and machine learning have improved free resolution by optimizing image reconstruction across diverse resolutions and scales.
Future Trends in Algebraic Resolutions
Future trends in algebraic resolutions emphasize enhanced cellular resolutions for improved computational efficiency and geometric insight over traditional free resolutions, which often become infeasible for large-scale problems. Advances in combinatorial methods and homological algebra facilitate more compact cellular structures, enabling finer algebraic invariant computations and deeper connections with topological data analysis. These developments point toward scalable algorithms leveraging cellular frameworks to address complex algebraic varieties and modules with greater precision.
Cellular resolution Infographic
 libterm.com
libterm.com