Haar measure provides a rigorous way to define a consistent measure on locally compact topological groups, allowing integration over these spaces. This measure is invariant under group translation, making it fundamental in areas such as harmonic analysis and representation theory. Explore the rest of the article to understand how Haar measure underpins key mathematical concepts and applications.
Table of Comparison
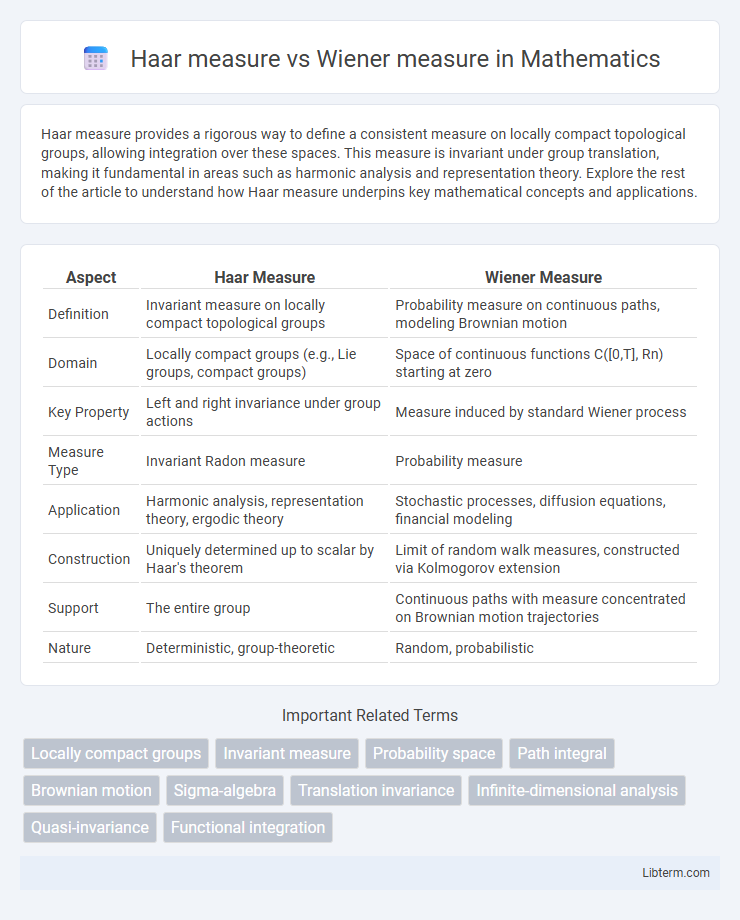
| Aspect | Haar Measure | Wiener Measure |
|---|---|---|
| Definition | Invariant measure on locally compact topological groups | Probability measure on continuous paths, modeling Brownian motion |
| Domain | Locally compact groups (e.g., Lie groups, compact groups) | Space of continuous functions C([0,T], Rn) starting at zero |
| Key Property | Left and right invariance under group actions | Measure induced by standard Wiener process |
| Measure Type | Invariant Radon measure | Probability measure |
| Application | Harmonic analysis, representation theory, ergodic theory | Stochastic processes, diffusion equations, financial modeling |
| Construction | Uniquely determined up to scalar by Haar's theorem | Limit of random walk measures, constructed via Kolmogorov extension |
| Support | The entire group | Continuous paths with measure concentrated on Brownian motion trajectories |
| Nature | Deterministic, group-theoretic | Random, probabilistic |
Introduction to Haar Measure and Wiener Measure
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, fundamental for harmonic analysis and representation theory. Wiener measure is a probability measure on the space of continuous functions, essential in modeling Brownian motion and stochastic processes. Both measures serve distinct purposes: Haar measure enables integration over groups, while Wiener measure facilitates probabilistic analysis of continuous paths.
Defining Haar Measure: Key Concepts
Haar measure is a unique, translation-invariant measure defined on locally compact topological groups, ensuring a consistent way to integrate functions over group elements. It provides a foundation for harmonic analysis by assigning equal measure to all translates of a set, crucial for studying symmetry and group actions. Unlike Wiener measure, which models probability distributions of Brownian motion paths, Haar measure operates in abstract algebraic contexts, emphasizing invariance rather than stochastic properties.
Understanding Wiener Measure: Essential Features
Wiener measure is a probability measure on the space of continuous paths, essential for modeling Brownian motion and stochastic processes in functional analysis. It assigns probabilities to sets of continuous functions, capturing the randomness and temporal evolution of Brownian paths. Unlike Haar measure, which is invariant under group actions in locally compact groups, Wiener measure incorporates the temporal structure and path continuity crucial for stochastic calculus and diffusion process modeling.
Mathematical Foundations of Haar and Wiener Measures
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, fundamental in harmonic analysis and abstract algebra for integrating functions over groups. Wiener measure, constructed on the space of continuous paths, provides a probability measure modeling Brownian motion, essential in stochastic processes and functional analysis. The mathematical foundation of Haar measure relies on group structure and invariance properties, while Wiener measure is grounded in Gaussian processes and the topology of path spaces.
Invariance Properties: Haar vs. Wiener Measure
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, ensuring that the measure of a set remains unchanged under group translations. Wiener measure, defined on the space of continuous paths, lacks strict translation invariance but exhibits invariance under time shifts and certain transformations related to Brownian motion increments. The fundamental difference lies in Haar measure's strict invariance under group actions, while Wiener measure's invariance is expressed through stochastic symmetries inherent to Brownian motion paths.
Applications in Probability and Analysis
Haar measure, a unique translation-invariant measure on locally compact groups, provides a fundamental tool for analyzing symmetries and invariant probabilities in harmonic analysis and ergodic theory. Wiener measure governs the distribution of continuous paths in Brownian motion, playing a crucial role in stochastic processes, diffusion analysis, and the study of Gaussian measures in infinite-dimensional spaces. Applications in probability leverage Haar measure for random walks on groups, while Wiener measure underpins stochastic calculus and the modeling of continuous-time Markov processes.
Topological Groups and Haar Measure
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, enabling integration of functions while respecting group symmetries. It serves as a foundational tool in harmonic analysis and representation theory, providing a way to generalize Lebesgue measure to non-abelian groups. In contrast, Wiener measure arises in the study of Brownian motion on function spaces and is fundamentally probabilistic rather than algebraic or topological.
Stochastic Processes and Wiener Measure
Wiener measure is a foundational probability measure defined on the space of continuous functions, central to modeling Brownian motion in stochastic processes. It captures the distribution of paths generated by a Wiener process, facilitating the analysis of diffusion and random walk phenomena. Haar measure, in contrast, is a translation-invariant measure on locally compact groups and is not typically applied to path spaces, highlighting the distinctive roles these measures play in stochastic analysis and harmonic analysis.
Comparing Use Cases: Haar vs. Wiener in Practice
Haar measure is essential in harmonic analysis and group theory for integrating functions over compact topological groups, enabling the study of invariant measures under group actions. Wiener measure is primarily used in probability theory and stochastic processes to model Brownian motion paths on continuous function spaces. While Haar measure facilitates symmetry-based analysis on groups, Wiener measure provides a rigorous foundation for continuous-time random processes and diffusions in mathematical physics and finance.
Summary: Key Differences and Connections
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, facilitating integration over group elements with a focus on symmetry and algebraic structure. Wiener measure, in contrast, is a probability measure on the space of continuous paths, underpinning Brownian motion and stochastic processes with an emphasis on time-evolution and randomness. The connection lies in their roles as foundational tools in harmonic analysis and probability theory, where Haar measure supports group symmetries and Wiener measure models stochastic behavior on function spaces.
Haar measure Infographic
 libterm.com
libterm.com