Differential equations describe the relationship between a function and its derivatives, playing a crucial role in modeling continuous change in fields like physics, engineering, and biology. Solving these equations helps predict system behavior over time, enabling deeper insights into dynamic processes. Explore the rest of this article to understand different types of differential equations and their practical applications.
Table of Comparison
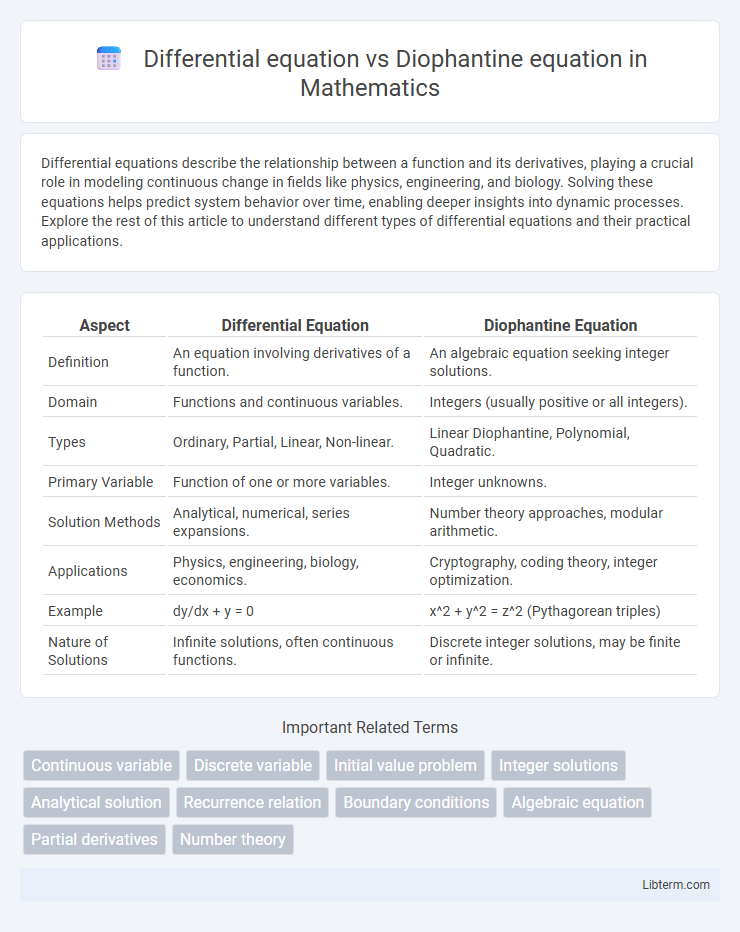
| Aspect | Differential Equation | Diophantine Equation |
|---|---|---|
| Definition | An equation involving derivatives of a function. | An algebraic equation seeking integer solutions. |
| Domain | Functions and continuous variables. | Integers (usually positive or all integers). |
| Types | Ordinary, Partial, Linear, Non-linear. | Linear Diophantine, Polynomial, Quadratic. |
| Primary Variable | Function of one or more variables. | Integer unknowns. |
| Solution Methods | Analytical, numerical, series expansions. | Number theory approaches, modular arithmetic. |
| Applications | Physics, engineering, biology, economics. | Cryptography, coding theory, integer optimization. |
| Example | dy/dx + y = 0 | x^2 + y^2 = z^2 (Pythagorean triples) |
| Nature of Solutions | Infinite solutions, often continuous functions. | Discrete integer solutions, may be finite or infinite. |
Introduction to Differential and Diophantine Equations
Differential equations involve functions and their derivatives, describing continuous systems such as physics and engineering models, while Diophantine equations concern integer solutions to polynomial equations, fundamental in number theory and discrete mathematics. Differential equations are classified into ordinary and partial types, emphasizing analytical methods and existence of solutions, whereas Diophantine equations focus on finding integer or rational solutions, often requiring combinatorial or algebraic approaches. Understanding these two equation classes highlights the contrast between continuous change modeling and discrete solution constraints in advanced mathematics.
Fundamental Concepts and Definitions
Differential equations involve functions and their derivatives, representing relationships that describe rates of change and continuous processes, essential in modeling physical phenomena such as motion, heat transfer, and fluid dynamics. Diophantine equations consist of polynomial equations with integer coefficients seeking integer solutions, central to number theory and integral solutions in algebraic structures. Understanding the nature of solutions--continuous functions for differential equations and discrete integers for Diophantine equations--highlights the fundamental conceptual divergence between these two mathematical fields.
Key Differences Between Differential and Diophantine Equations
Differential equations involve functions and their derivatives, modeling continuous change and rates in fields like physics and engineering, whereas Diophantine equations focus on polynomial equations requiring integer solutions, significant in number theory. Differential equations typically involve infinite solution sets expressed in functional form, while Diophantine equations have discrete solutions limited to integer values. The methods of solving differ fundamentally: differential equations use calculus-based techniques, and Diophantine equations rely on algebraic or number-theoretic approaches such as modular arithmetic.
Applications in Science and Engineering
Differential equations model continuous dynamic systems such as heat transfer, fluid flow, and electrical circuits in engineering, enabling precise predictions and control of physical phenomena. Diophantine equations solve integer-based problems in cryptography, coding theory, and network design by finding solutions that satisfy specific discrete constraints. Both types of equations play critical roles in optimizing system behaviors and solving practical problems across scientific and technological domains.
Methods of Solution
Differential equations are solved using methods such as separation of variables, integrating factors, and characteristic equations for linear cases, often involving calculus techniques. Diophantine equations require integer solutions and are addressed through number theory methods like the Euclidean algorithm, modular arithmetic, and the use of continued fractions. While differential equations emphasize continuous functions and derivatives, Diophantine equations focus on discrete integer solutions with algebraic and arithmetic tools.
Role in Pure and Applied Mathematics
Differential equations model continuous processes and change rates, playing a fundamental role in applied mathematics, physics, and engineering to describe dynamic systems. Diophantine equations, involving integer solutions, are central to pure mathematics, particularly number theory, addressing problems of solvability and integer constraints. Both types of equations underpin theoretical frameworks but diverge in applications, with differential equations driving modeling and prediction, while Diophantine equations focus on discrete structures and algebraic properties.
Examples of Differential Equations
Differential equations describe the relationship between a function and its derivatives, such as the classic example dy/dx = 3x^2, representing the rate of change of y with respect to x. Another key example is the second-order linear differential equation d^2y/dx^2 + 4y = 0, modeling simple harmonic motion in physics. These equations contrast with Diophantine equations, which seek integer solutions, exemplified by the equation x^2 + y^2 = z^2 in number theory.
Examples of Diophantine Equations
Diophantine equations involve finding integer solutions to polynomial equations, such as the classic example \(x^2 + y^2 = z^2\), which represents Pythagorean triples. Another notable instance is Fermat's Last Theorem equation \(x^n + y^n = z^n\) for \(n > 2\), where no non-zero integer solutions exist. In contrast, differential equations like \(\frac{dy}{dx} = ky\) seek functions as solutions and involve calculus rather than strictly integer solutions.
Challenges in Solving Each Type
Differential equations present challenges due to their dependence on continuous variables and the need for methods like separation of variables, integrating factors, or numerical approximations to find solutions. Diophantine equations, involving integer solutions to polynomial equations, pose difficulties because of the discrete solution space and the lack of general solution methods, often requiring number theory techniques or modular arithmetic. Both types demand specialized approaches but differ fundamentally in the nature of their solution sets and applicable mathematical tools.
Summary and Comparative Analysis
Differential equations involve functions and their derivatives, describing continuous change and modeling phenomena in physics, engineering, and biology, while Diophantine equations focus on finding integer solutions to polynomial equations, primarily studied in number theory. Differential equations use calculus-based methods and numerical approximations, whereas Diophantine equations rely on algebraic techniques and integer constraints, often involving methods from algebraic geometry and arithmetic. The key distinction lies in their applications and solution sets: differential equations address dynamic systems with real-valued functions, whereas Diophantine equations are discrete problems centered on integral solutions.
Differential equation Infographic
 libterm.com
libterm.com