Embedding enhances machine learning models by transforming complex data into vector representations that capture semantic relationships. This process improves your system's ability to understand context and meaning across various data types, such as text, images, and audio. Explore the rest of the article to discover how embedding techniques can optimize your AI projects.
Table of Comparison
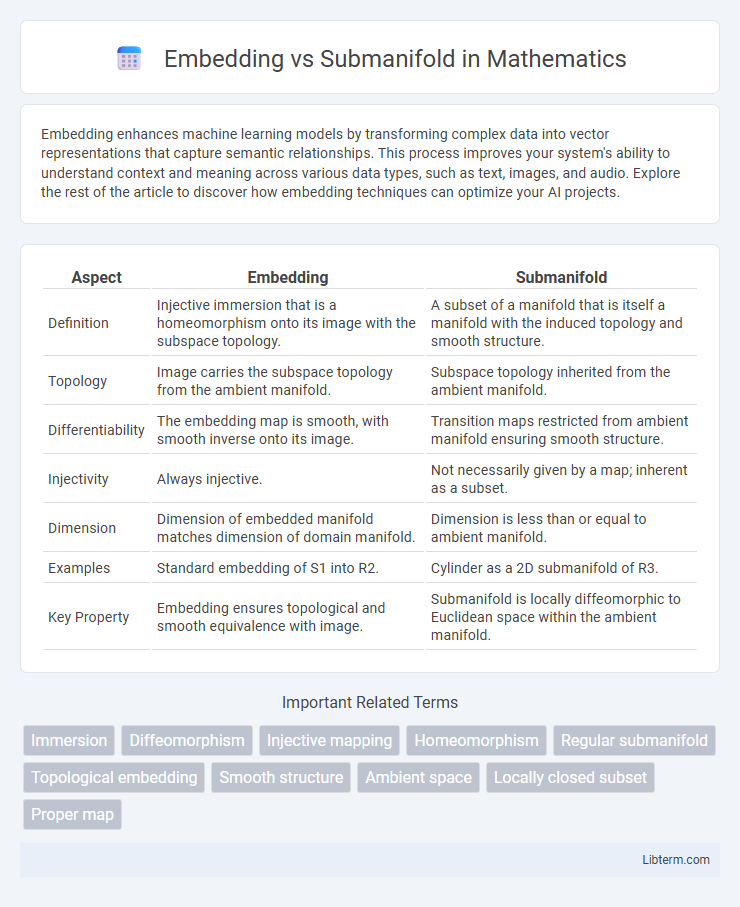
| Aspect | Embedding | Submanifold |
|---|---|---|
| Definition | Injective immersion that is a homeomorphism onto its image with the subspace topology. | A subset of a manifold that is itself a manifold with the induced topology and smooth structure. |
| Topology | Image carries the subspace topology from the ambient manifold. | Subspace topology inherited from the ambient manifold. |
| Differentiability | The embedding map is smooth, with smooth inverse onto its image. | Transition maps restricted from ambient manifold ensuring smooth structure. |
| Injectivity | Always injective. | Not necessarily given by a map; inherent as a subset. |
| Dimension | Dimension of embedded manifold matches dimension of domain manifold. | Dimension is less than or equal to ambient manifold. |
| Examples | Standard embedding of S1 into R2. | Cylinder as a 2D submanifold of R3. |
| Key Property | Embedding ensures topological and smooth equivalence with image. | Submanifold is locally diffeomorphic to Euclidean space within the ambient manifold. |
Introduction to Embeddings and Submanifolds
Embeddings refer to maps from one manifold into another that preserve the topological and differentiable structure, allowing a manifold to be represented within a higher-dimensional space without intersection or distortion. Submanifolds are subsets of manifolds that themselves carry a manifold structure compatible with the ambient space, often classified as embedded or immersed based on how they relate to the enclosing manifold. Understanding embeddings and submanifolds is fundamental in differential geometry for analyzing manifold properties through their representations and intrinsic structure within larger spaces.
Defining Embeddings in Differential Geometry
In differential geometry, defining embeddings involves smooth injective immersions of manifolds that are homeomorphisms onto their images, ensuring the embedded manifold inherits the subspace topology. An embedding preserves geometric properties by embedding a lower-dimensional manifold into a higher-dimensional one without self-intersections, differentiating it from general immersions. Submanifolds, often realized as embedded manifolds, maintain compatibility between their intrinsic differential structure and the ambient space, highlighting the role of embeddings in manifold theory.
Understanding Submanifolds: Key Concepts
Submanifolds are subsets of a manifold that inherit a consistent differentiable structure, allowing them to be analyzed using the tools of differential geometry. The key concept involves the embedding map, a smooth injective immersion that provides a topological embedding, ensuring the submanifold's intrinsic properties are preserved within the ambient space. Understanding the distinction between an embedding and a submanifold centers on the submanifold's ability to locally resemble Euclidean space while being globally situated inside a higher-dimensional manifold.
Mathematical Formalism: Embedding vs Submanifold
An embedding is a smooth map \( f: M \to N \) between manifolds where \( M \) is homeomorphic to its image \( f(M) \) and the differential \( df_p \) is injective at every point \( p \in M \), ensuring \( f(M) \) is an embedded submanifold of \( N \). A submanifold is defined intrinsically as a subset \( S \subset N \) equipped with a manifold structure such that the inclusion map \( i: S \hookrightarrow N \) is an embedding, meaning the topology and smooth structure on \( S \) are induced from \( N \). The mathematical distinction lies in viewing embeddings as maps with injective differentials producing submanifolds, whereas submanifolds are subsets recognized by the embedding property of their inclusion into ambient spaces.
Topological Implications of Embeddings
Embeddings preserve topological properties by providing a homeomorphic image of one space within another, ensuring that local and global structures remain intact without distortion or self-intersection. Submanifolds, while smoothly embedded, may inherit different intrinsic topological features depending on the ambient manifold's geometry, impacting properties like compactness and connectedness. Understanding the topological implications of embeddings is crucial for applications in differential geometry and manifold theory, as it guarantees the faithful representation of the embedded manifold's topology within a higher-dimensional space.
Examples: Recognizing Embeddings and Submanifolds
Embedding occurs when a lower-dimensional manifold is smoothly and injectively placed within a higher-dimensional manifold, exemplified by a circle embedded into a plane without self-intersections. Submanifolds, such as a sphere defined by the zero set of a smooth function in Euclidean space, are subsets that inherit manifold structure from the ambient space. Recognizing embeddings involves checking smoothness and injectivity, while identifying submanifolds often requires verifying the regular value theorem or implicit function conditions.
Differences in Structure and Properties
Embedding involves mapping a lower-dimensional manifold into a higher-dimensional space while preserving topological properties, resulting in an injective and smooth immersion. Submanifold refers to a subset of a manifold that inherits the surrounding manifold's differential structure, often characterized by being a regularly embedded or immersed manifold with the induced topology. Differences in structure arise as embeddings ensure global injectivity and topological equivalence, whereas submanifolds may exhibit local immersion without global injectivity or may not be embedded with a standard subspace topology.
Applications in Mathematics and Physics
Embedding maps a lower-dimensional manifold into a higher-dimensional space preserving topological and geometric properties, crucial in differential geometry for visualizing complex shapes and in general relativity to represent curved spacetime. Submanifolds are subsets of manifolds that inherit properties from the ambient space, extensively used in gauge theory and string theory to analyze fields and branes constrained to specific regions. Both concepts facilitate understanding manifold structures and their interactions, enabling advancements in areas like topology, quantum field theory, and cosmology.
Common Misconceptions and Clarifications
Embedding is often misunderstood as merely an injective function, but it specifically requires a homeomorphism onto its image, preserving topological structure, unlike general immersions. Submanifolds are frequently confused with embedded submanifolds; submanifolds need not be embedded and can have more flexible local behaviors such as being immersed but not embedded. Clarifying these distinctions helps avoid misconceptions around the smoothness and topological properties inherent to embeddings versus more general submanifold concepts.
Conclusion: Choosing Between Embedding and Submanifold
Choosing between embedding and submanifold depends on the application's geometric requirements and computational complexity. Embeddings ensure global injectivity and smoothness, making them ideal for preserving intrinsic manifold structures in higher-dimensional spaces. Submanifolds provide flexibility for local analysis and lower-dimensional representations but may lack the global properties essential for certain machine learning or visualization tasks.
Embedding Infographic
 libterm.com
libterm.com