A fully invariant submodule is a submodule that remains stable under every endomorphism of its parent module, ensuring that any module homomorphism maps elements within this submodule back into it. This property makes fully invariant submodules critical in understanding the structure and behavior of modules in algebra. Explore the rest of the article to deepen your knowledge about fully invariant submodules and their applications.
Table of Comparison
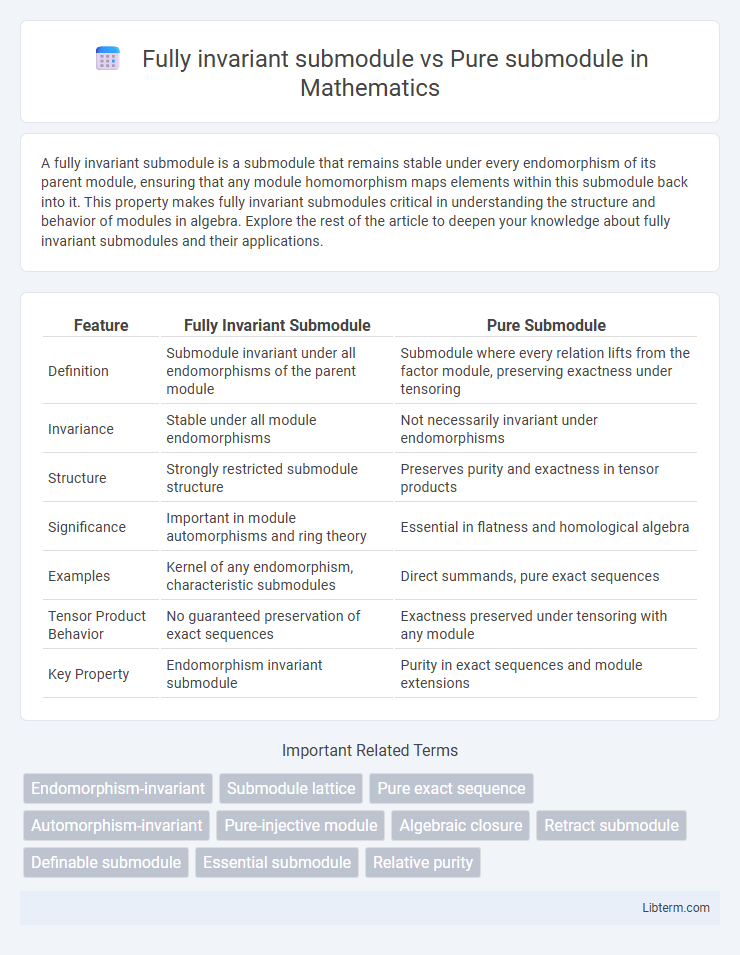
| Feature | Fully Invariant Submodule | Pure Submodule |
|---|---|---|
| Definition | Submodule invariant under all endomorphisms of the parent module | Submodule where every relation lifts from the factor module, preserving exactness under tensoring |
| Invariance | Stable under all module endomorphisms | Not necessarily invariant under endomorphisms |
| Structure | Strongly restricted submodule structure | Preserves purity and exactness in tensor products |
| Significance | Important in module automorphisms and ring theory | Essential in flatness and homological algebra |
| Examples | Kernel of any endomorphism, characteristic submodules | Direct summands, pure exact sequences |
| Tensor Product Behavior | No guaranteed preservation of exact sequences | Exactness preserved under tensoring with any module |
| Key Property | Endomorphism invariant submodule | Purity in exact sequences and module extensions |
Introduction to Submodules in Module Theory
In module theory, a fully invariant submodule is a submodule that remains invariant under every endomorphism of the parent module, ensuring maximal structural stability. Pure submodules are defined by their preservation of system solvability, characterized by exact sequences that remain exact upon tensoring with any module. Understanding the distinction between fully invariant and pure submodules provides insight into module homomorphisms and the internal structure of modules in algebra.
Defining Fully Invariant Submodules
A fully invariant submodule of a module \( M \) is a submodule \( N \) such that every endomorphism of \( M \) maps \( N \) into itself, ensuring invariance under all module homomorphisms from \( M \) to \( M \). This property is stronger than that of pure submodules, which require only the preservation of exact sequences under tensoring with arbitrary modules. Fully invariant submodules play a crucial role in the structure theory of modules, particularly in the context of module endomorphisms and decomposition.
Understanding Pure Submodules
Pure submodules are characterized by the preservation of exact sequences under tensoring, ensuring that for any module M, the tensor product with a pure submodule remains exact, which is essential for understanding their structural stability in module theory. Unlike fully invariant submodules, which are stable under all endomorphisms of the parent module, pure submodules emphasize compatibility with tensor operations and homological properties. This distinction highlights that pure submodules maintain the integrity of algebraic relationships in extension and base change processes, making them crucial in homological algebra and module theory.
Key Differences Between Fully Invariant and Pure Submodules
Fully invariant submodules are submodules preserved under every endomorphism of the parent module, reflecting a strong form of structural stability within module theory. Pure submodules, on the other hand, satisfy the condition that tensoring with any module preserves exact sequences, emphasizing homological purity rather than endomorphism invariance. The key difference lies in their defining properties: fully invariant submodules are characterized by endomorphism-invariance, while pure submodules are identified through the preservation of exactness in tensor products.
Algebraic Properties and Preservation Under Homomorphisms
A fully invariant submodule remains stable under all endomorphisms of the parent module, ensuring algebraic properties like closure under module homomorphisms are preserved universally. In contrast, a pure submodule maintains exactness when tensored with any module, highlighting its preservation of flatness and structural decompositions rather than invariance under arbitrary endomorphisms. Fully invariant submodules are essential in studying module automorphisms, while pure submodules play a crucial role in extension problems and tensor product behavior.
Structural Examples Illustrating Each Submodule
Fully invariant submodules are those preserved under all endomorphisms of the module, exemplified structurally by the socle in a semisimple module where every homomorphism fixes simple submodules. Pure submodules maintain solution sets of linear equations, as demonstrated in the rational numbers Q as a pure submodule of the real numbers R, reflecting the preservation of divisibility relations. These examples highlight the distinction: fully invariant submodules emphasize endomorphism stability, while pure submodules focus on algebraic purity and system solvability within module extensions.
Connections to Module Homomorphisms and Endomorphisms
Fully invariant submodules remain stable under every endomorphism of the parent module, highlighting a strong connection to module endomorphisms and reflecting intrinsic symmetry within the module's structure. Pure submodules, characterized by preservation under tensoring with arbitrary modules, link to module homomorphisms through exact sequences and flatness conditions, ensuring solutions to systems of linear equations lift accurately. The interplay between fully invariant and pure submodules reveals nuanced behavior in module homomorphisms, where fully invariant submodules offer rigidity under endomorphisms while pure submodules facilitate flexible embedding and extension properties.
Role in Module Decomposition and Classification
Fully invariant submodules serve as critical tools in module decomposition due to their stability under all endomorphisms, enabling refined classification through intrinsic structural invariants. Pure submodules, characterized by their exact sequence preservation and tensor product compatibility, facilitate decomposition by maintaining module properties essential for extensions and direct summand analysis. Both concepts play complementary roles in classifying modules: fully invariant submodules provide canonical decompositions aligned with endomorphic actions, while pure submodules ensure decompositions preserve module-theoretic properties key to purity-based classifications.
Applications in Ring and Module Theory
Fully invariant submodules, characterized by their stability under all endomorphisms of a module, play a crucial role in the structural analysis of modules over rings, aiding in the classification and decomposition of modules. Pure submodules, defined by the preservation of exact sequences upon tensoring, are fundamental in studying flat modules and homological dimensions, providing insights into extensions and purity in module theory. Both concepts are integral in understanding the behavior of modules under morphisms and tensor products, impacting the development of ring theoretic properties and categorical frameworks in algebra.
Summary and Further Research Directions
Fully invariant submodules, invariant under all endomorphisms of the parent module, exhibit strong stability properties essential for studying module structure and decomposition. Pure submodules, defined by the preservation of exact sequences under tensoring, facilitate analysis in homological algebra and model theory, revealing insights into direct limits and flatness conditions. Future research may explore the interplay between these submodules in broader module categories, investigate their roles within non-abelian contexts, and develop computational methods for characterizing invariance and purity in complex algebraic systems.
Fully invariant submodule Infographic
 libterm.com
libterm.com