The L1 norm, also known as the Manhattan norm or taxicab norm, measures the sum of the absolute values of a vector's components, making it essential for sparse data representation and robust regression models. It is widely used in machine learning for feature selection and regularization techniques such as LASSO, where minimizing the L1 norm encourages sparsity. Explore the rest of this article to understand how the L1 norm can enhance your data analysis and model performance.
Table of Comparison
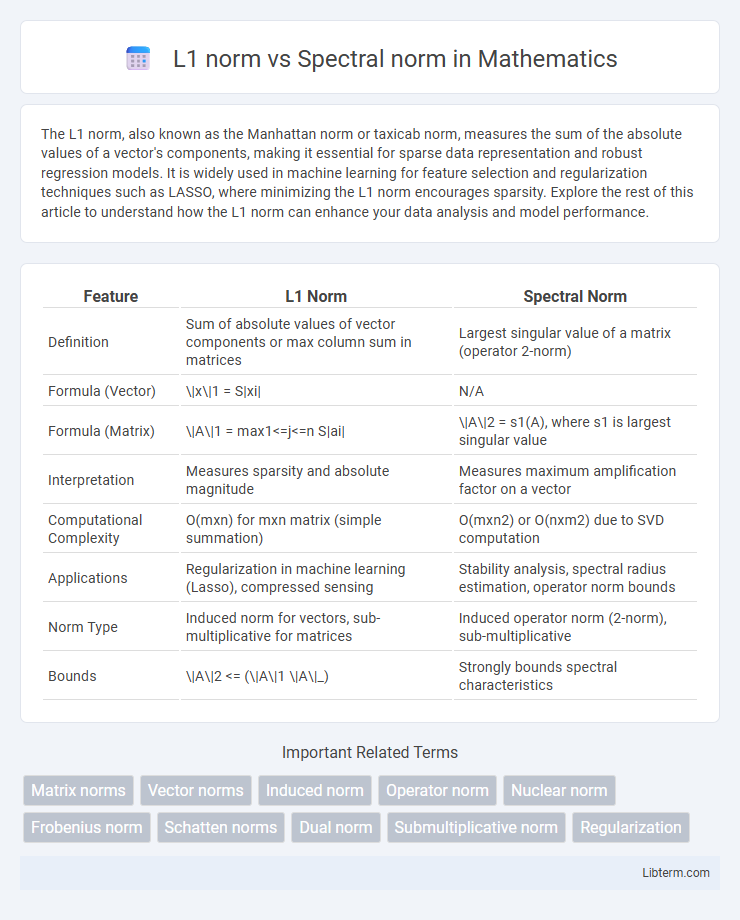
| Feature | L1 Norm | Spectral Norm |
|---|---|---|
| Definition | Sum of absolute values of vector components or max column sum in matrices | Largest singular value of a matrix (operator 2-norm) |
| Formula (Vector) | \|x\|1 = S|xi| | N/A |
| Formula (Matrix) | \|A\|1 = max1<=j<=n S|ai| | \|A\|2 = s1(A), where s1 is largest singular value |
| Interpretation | Measures sparsity and absolute magnitude | Measures maximum amplification factor on a vector |
| Computational Complexity | O(mxn) for mxn matrix (simple summation) | O(mxn2) or O(nxm2) due to SVD computation |
| Applications | Regularization in machine learning (Lasso), compressed sensing | Stability analysis, spectral radius estimation, operator norm bounds |
| Norm Type | Induced norm for vectors, sub-multiplicative for matrices | Induced operator norm (2-norm), sub-multiplicative |
| Bounds | \|A\|2 <= (\|A\|1 \|A\|_) | Strongly bounds spectral characteristics |
Introduction to Matrix Norms
Matrix norms quantify the size or length of a matrix, serving as essential tools in numerical analysis and machine learning. The L1 norm, defined as the maximum absolute column sum, emphasizes sparsity and simplicity, while the spectral norm, equivalent to the largest singular value, measures the maximum stretching factor of the matrix. Understanding the differences between L1 norm and spectral norm aids in selecting appropriate norms for regularization, stability analysis, and optimization tasks in linear algebra applications.
Overview of L1 Norm
The L1 norm, also known as the Manhattan norm, measures the sum of the absolute values of a vector's components, making it useful for promoting sparsity in machine learning models. It is often applied in regularization techniques like Lasso regression to encourage feature selection by shrinking less important coefficients to zero. In contrast to the spectral norm, which captures the largest singular value and reflects matrix operator behavior, the L1 norm focuses on element-wise magnitude, providing a robust measure for vector sparsity and interpretability.
Overview of Spectral Norm
The spectral norm of a matrix, defined as the largest singular value, measures the maximum stretching factor the matrix can apply to a vector, making it crucial in understanding operator behavior in linear algebra. Unlike the L1 norm, which sums absolute values typically of vector elements and emphasizes sparsity, the spectral norm captures the matrix's intrinsic geometric distortion properties. It is widely used in machine learning and numerical analysis for stability assessment and regularization in deep learning models.
Mathematical Definitions
The L1 norm of a matrix, also known as the maximum absolute column sum norm, is defined as the maximum sum of the absolute values of the matrix entries in any column, mathematically expressed as ||A||1 = max_j _i |a_ij| for a matrix A. The spectral norm, or operator 2-norm, corresponds to the largest singular value of the matrix, defined as ||A||2 = max_{x 0} (||Ax||2 / ||x||2), which equals the square root of the largest eigenvalue of A^T A. While the L1 norm measures the maximum column-wise magnitude, the spectral norm captures the maximum amplification factor of the matrix when acting as a linear operator on vectors.
Key Differences Between L1 and Spectral Norms
L1 norm measures the sum of absolute values of a matrix's entries, emphasizing sparse solutions by promoting zeros in vector representations, while the spectral norm represents the largest singular value, indicating the maximum stretching factor of the matrix in any direction. L1 norm is widely used in regularization to enforce sparsity in machine learning models, whereas spectral norm is crucial in stability analysis and controlling Lipschitz constants in deep neural networks. The key difference lies in L1 norm focusing on element-wise magnitude, while spectral norm captures global matrix behavior through eigenvalue or singular value decomposition.
Computational Complexity Comparison
The L1 norm computation involves summing the absolute values of all matrix elements, resulting in a time complexity of O(mn) for an m by n matrix, making it computationally straightforward and efficient. In contrast, the spectral norm requires calculating the largest singular value via singular value decomposition or power iteration methods, with a higher complexity typically around O(mn^2) for dense matrices. Consequently, the L1 norm is preferred in scenarios requiring faster computations, while the spectral norm provides more detailed spectral properties at a greater computational cost.
Use Cases and Applications
L1 norm is widely used in feature selection, sparse coding, and regularization techniques such as Lasso regression due to its ability to promote sparsity by penalizing the absolute sum of coefficients. Spectral norm, which measures the largest singular value of a matrix, finds critical applications in stability analysis of neural networks, control theory, and matrix perturbation studies by bounding operator growth. In deep learning, L1 norm aids in feature interpretability and compression, while spectral norm is essential for controlling Lipschitz constants to ensure robust training and generalization.
Advantages and Disadvantages
L1 norm offers sparsity promotion and robustness to outliers, making it ideal for feature selection and compressed sensing, but it may overlook correlations between features. Spectral norm captures the largest singular value of a matrix, providing insights into stability and sensitivity in linear transformations, though it is computationally intensive and less effective for inducing sparsity. Choosing between L1 and spectral norms depends on whether sparsity or operator stability is prioritized in the application.
Practical Considerations in Machine Learning
L1 norm promotes sparsity by penalizing the sum of absolute values of parameters, making it effective for feature selection and model interpretability in machine learning. Spectral norm controls the largest singular value of weight matrices, enhancing model stability and improving generalization, especially in deep neural networks. Choosing between L1 and spectral norm depends on whether sparsity or Lipschitz continuity is prioritized in specific applications like regularization and robustness.
Conclusion and Recommendations
The L1 norm measures matrix sparsity by summing absolute values of elements while the spectral norm captures the largest singular value, indicating maximum stretching effect in linear transformations. For applications requiring robustness to sparse noise or promoting sparsity, the L1 norm is preferable, whereas the spectral norm suits stability analysis and bounding operator behavior. Selecting the norm depends on whether focus lies on element-wise magnitude effects (L1 norm) or spectral properties dictating system response (spectral norm).
L1 norm Infographic
 libterm.com
libterm.com