The Cantor set is a fractal formed by repeatedly removing the middle third from a line segment, resulting in a highly intricate structure with zero length but uncountably many points. This mathematical construct demonstrates key concepts in topology, measure theory, and chaos theory, making it a fundamental example in understanding fractal geometry. Explore the rest of this article to uncover how the Cantor set challenges conventional notions of size and dimension.
Table of Comparison
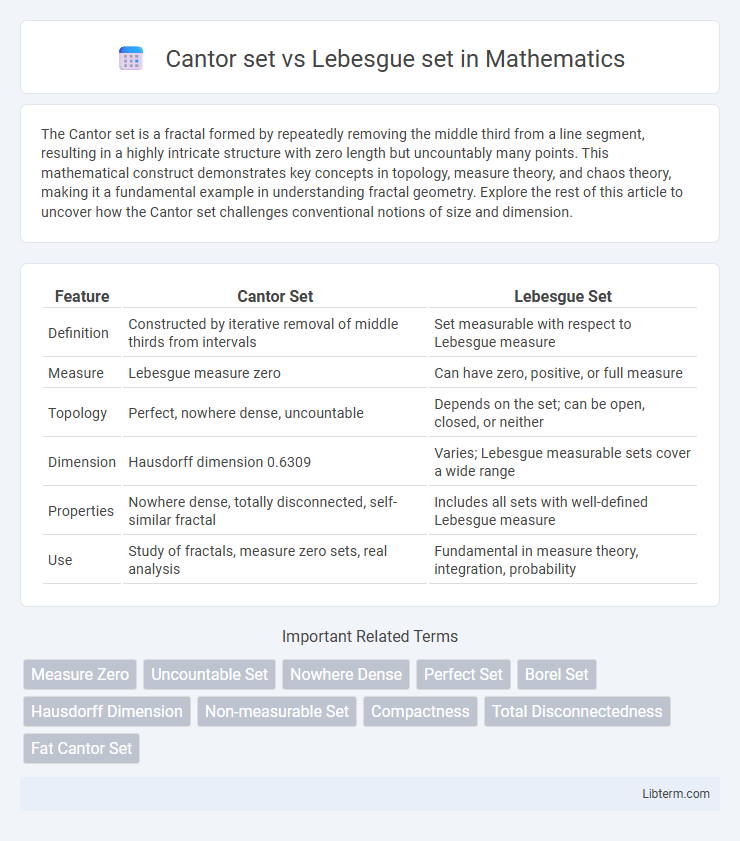
| Feature | Cantor Set | Lebesgue Set |
|---|---|---|
| Definition | Constructed by iterative removal of middle thirds from intervals | Set measurable with respect to Lebesgue measure |
| Measure | Lebesgue measure zero | Can have zero, positive, or full measure |
| Topology | Perfect, nowhere dense, uncountable | Depends on the set; can be open, closed, or neither |
| Dimension | Hausdorff dimension 0.6309 | Varies; Lebesgue measurable sets cover a wide range |
| Properties | Nowhere dense, totally disconnected, self-similar fractal | Includes all sets with well-defined Lebesgue measure |
| Use | Study of fractals, measure zero sets, real analysis | Fundamental in measure theory, integration, probability |
Introduction to Cantor Set and Lebesgue Set
The Cantor set is a classic example of a fractal and uncountably infinite set formed by repeatedly removing the middle third of line segments, showcasing properties such as perfectness and nowhere density. The Lebesgue set relates to Lebesgue measure theory, representing measurable subsets of real numbers where notions of length and integration are well-defined. Understanding the Cantor set provides insight into complex set constructions, while the Lebesgue set underpins modern measure theory and the foundation for Lebesgue integration.
Historical Background and Mathematical Origins
The Cantor set, introduced by Georg Cantor in 1883, originated from his work on point-set topology and set theory, emphasizing the construction of a perfect, nowhere dense set with zero measure. The Lebesgue set emerged from Henri Lebesgue's early 20th-century efforts to generalize integration theory, leading to the concept of Lebesgue measure and measurable sets that extended beyond traditional Riemann integration. These foundational developments shaped modern analysis by contrasting pathological examples like the Cantor set with measure-theoretic frameworks established by Lebesgue.
Construction of the Cantor Set
The Cantor set is constructed by iteratively removing the open middle third from each interval, starting with the unit interval [0, 1], resulting in a fractal set with zero Lebesgue measure. This process involves an infinite number of steps, leaving a perfect, totally disconnected, uncountable set that is nowhere dense in the real line. In contrast, the Lebesgue measure assesses the "size" of sets, assigning a measure of zero to the Cantor set despite its uncountable cardinality.
Properties and Characteristics of the Cantor Set
The Cantor set is a perfect, nowhere dense, uncountably infinite subset of the real line characterized by its zero Lebesgue measure and self-similar fractal structure. Unlike the Lebesgue measurable sets, the Cantor set is constructed through an iterative process of removing middle thirds, resulting in a set that is totally disconnected yet compact. Its unique properties include being closed, having no intervals, and exhibiting a Hausdorff dimension less than 1, contrasting with the typical Lebesgue sets that often contain intervals and have positive measure.
Understanding the Lebesgue Set in Measure Theory
The Lebesgue set in measure theory refers to the collection of points where a measurable function behaves "regularly" with respect to local averages, characterized by the Lebesgue differentiation theorem. Unlike the Cantor set, which is a fractal set with zero Lebesgue measure and perfect, nowhere dense structure, the Lebesgue set highlights points of approximate continuity of functions and their Lebesgue points. This distinction underscores the Lebesgue set's role in analyzing function behavior almost everywhere, contrasting with the Cantor set's significance in topology and measure as a measure-zero anomalous set.
Key Differences: Cantor Set vs Lebesgue Set
The Cantor set is a perfect, nowhere dense fractal created by repeatedly removing the middle thirds from a line segment, resulting in an uncountably infinite set with Lebesgue measure zero. In contrast, Lebesgue sets refer to measurable subsets of the real line with well-defined Lebesgue measure, often used to assess the size and integration properties of sets. Key differences include the Cantor set's zero Lebesgue measure despite its uncountable cardinality, while Lebesgue sets can have zero, positive, or infinite measure and are integral in measure theory and real analysis.
Dimensionality and Measure: Comparative Analysis
The Cantor set is a classic example of a fractal with zero Lebesgue measure but a Hausdorff dimension of approximately 0.6309, illustrating its complex self-similar structure despite having no "length" in the traditional sense. In contrast, Lebesgue measurable sets, such as intervals, typically have positive Lebesgue measure and integer dimensions corresponding to their topological dimensions. This comparative analysis highlights how the Cantor set challenges conventional notions of dimensionality and measure by exhibiting a non-integer fractal dimension while remaining measure-zero, unlike most Lebesgue measurable sets which have integer dimensions and non-zero measures.
Applications in Real Analysis and Probability
The Cantor set, a perfect, nowhere dense fractal with zero Lebesgue measure, is pivotal in real analysis for illustrating concepts like measure zero sets and non-countable sets, while its properties aid in constructing pathological examples of functions. The Lebesgue set, linked to the Lebesgue differentiation theorem, characterizes points where functions are differentiable almost everywhere, crucial for understanding absolute continuity and integral convergence in analysis. In probability theory, the Cantor set models distributions with singular continuous measures, whereas the Lebesgue set underpins measure-theoretic foundations for random variable behavior and integration.
Implications in Modern Mathematics
The Cantor set, a classic example of a fractal with zero Lebesgue measure, is fundamental in topology and measure theory, illustrating how uncountable sets can have null measure. Lebesgue measurable sets, central to integration theory, enable the formalization of the Lebesgue integral, which extends the Riemann integral and supports advanced analysis in probability and functional spaces. Understanding the distinction between these sets deepens insights into measure zero phenomena and supports the development of modern mathematical analysis, dynamical systems, and fractal geometry.
Conclusion: Significance of Comparing Cantor and Lebesgue Sets
Comparing Cantor and Lebesgue sets highlights key differences in measure theory and topology, where the Cantor set is uncountable with zero Lebesgue measure, exemplifying a fractal structure, while Lebesgue measurable sets extend to encompass a broader class including intervals with positive measure. This comparison underscores the Cantor set's role in demonstrating the limitations of classical notions of size and continuity within real analysis. Understanding these contrasts deepens insights into measure theory foundations and fractal geometry applications.
Cantor set Infographic
 libterm.com
libterm.com