Jordan measure is a mathematical concept used to determine the size of a set in Euclidean space, focusing on its boundary's behavior to establish measurability. It plays an essential role in real analysis by providing foundational understanding before more advanced measures like the Lebesgue measure are introduced. Explore the detailed explanation and applications of Jordan measure in the rest of the article to deepen your comprehension.
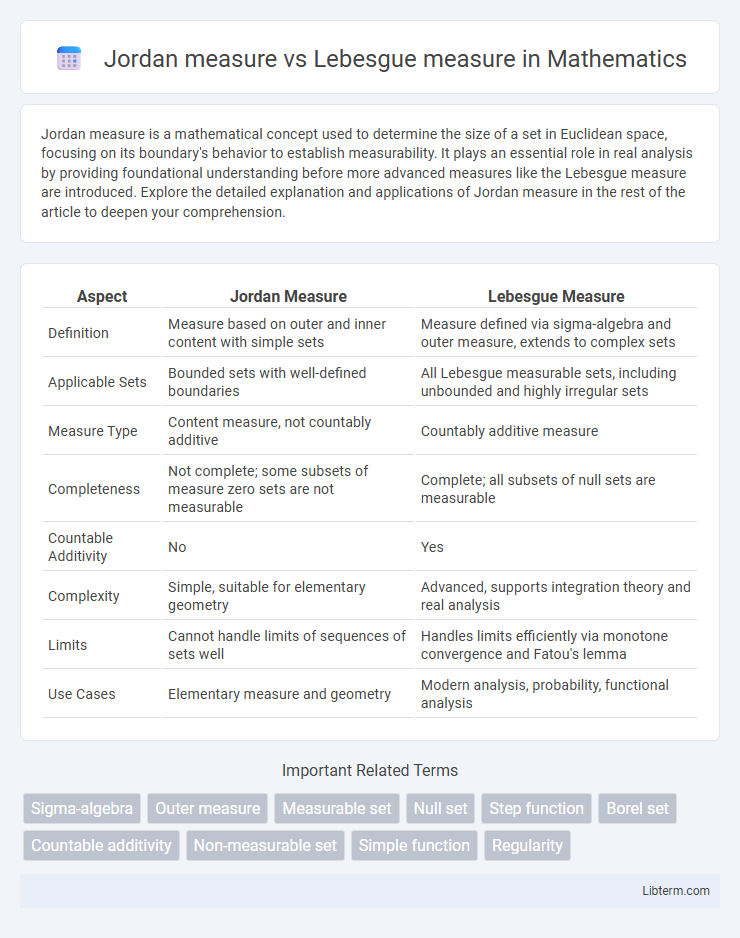
Table of Comparison
| Aspect | Jordan Measure | Lebesgue Measure |
|---|---|---|
| Definition | Measure based on outer and inner content with simple sets | Measure defined via sigma-algebra and outer measure, extends to complex sets |
| Applicable Sets | Bounded sets with well-defined boundaries | All Lebesgue measurable sets, including unbounded and highly irregular sets |
| Measure Type | Content measure, not countably additive | Countably additive measure |
| Completeness | Not complete; some subsets of measure zero sets are not measurable | Complete; all subsets of null sets are measurable |
| Countable Additivity | No | Yes |
| Complexity | Simple, suitable for elementary geometry | Advanced, supports integration theory and real analysis |
| Limits | Cannot handle limits of sequences of sets well | Handles limits efficiently via monotone convergence and Fatou's lemma |
| Use Cases | Elementary measure and geometry | Modern analysis, probability, functional analysis |
Introduction to Jordan and Lebesgue Measures
Jordan measure, an early concept in measure theory, assigns a set's size by approximating it with finite unions of rectangles, making it suitable for bounded, simple shapes. Lebesgue measure generalizes this concept by handling more complex sets, including those with irregular boundaries, through countable unions and limits, ensuring measure completeness. The Lebesgue measure extends Jordan measure by providing a more robust framework for integration and real analysis applications.
Historical Context and Motivation
The Jordan measure was developed in the late 19th century as part of efforts to formalize the concept of area for bounded sets in Euclidean space, particularly useful in geometric contexts where sets are well-behaved and have simple boundaries. It served as an early foundation before the introduction of the Lebesgue measure in 1902, which was motivated by the need to extend measure theory to more complex and irregular subsets, allowing for broader applications in analysis and integration. The Lebesgue measure generalized the Jordan measure by overcoming limitations related to countable additivity and the ability to measure more general sets, thus providing a more powerful and flexible framework for modern mathematical analysis.
Definition of Jordan Measure
Jordan measure, also known as Jordan content, is defined for bounded sets in Euclidean space where the boundary has measure zero, assigning a measure based on the approximation of the set by finite unions of rectangles. It relies on the concept of inner and outer approximations using "simple" sets to determine the measure, requiring the set to be Jordan measurable if these two approximations coincide. Unlike Lebesgue measure, Jordan measure is limited to sets with "nice" boundaries and is not complete, as it cannot measure all subsets of null sets.
Definition of Lebesgue Measure
Lebesgue measure is defined as a countably additive set function that extends the concept of length, area, and volume to more complex sets than those measurable by Jordan measure. Unlike Jordan measure, which applies only to sets with well-defined boundaries and excludes sets with complicated structures, Lebesgue measure can assign a measure to a broader class of sets, including those with fractal boundaries or countable unions of intervals. This generality makes Lebesgue measure fundamental in modern analysis, particularly in integration theory and probability.
Key Differences Between Jordan and Lebesgue Measures
Jordan measure is restricted to bounded sets with piecewise continuous boundaries and fails to measure sets with complex structures or infinite boundaries, whereas Lebesgue measure extends to a wider class of sets including unbounded and more irregular sets. Jordan measure is primarily constructed through finite sums of volumes of simple sets, limiting its applicability, while Lebesgue measure uses countable unions and limits, providing greater flexibility and robustness. Unlike Jordan measure, Lebesgue measure handles limit operations and convergence effectively, making it foundational in modern analysis and probability theory.
Examples: Sets with Jordan vs. Lebesgue Measurability
The Jordan measure applies effectively to simple sets like finite unions of rectangles, such as closed intervals [0,1] in \(\mathbb{R}\), whereas the Lebesgue measure extends to more complex or irregular sets like the Cantor set, which is Lebesgue measurable but not Jordan measurable. For example, the characteristic function of the rationals in [0,1] fails Jordan measurability due to boundary complexity but remains Lebesgue measurable with measure zero. Lebesgue measure thus includes a wider class of sets, particularly those with intricate boundaries or fractal structures, compared to the more restrictive Jordan measure.
Properties of Jordan Measure
Jordan measure is defined for bounded sets with boundaries of measure zero, making it suitable for simple geometric shapes. It is finitely additive but not countably additive, distinguishing it from Lebesgue measure, which extends to more complex sets through countable additivity. The Jordan measure is limited by its requirement for sets to be Jordan measurable, meaning the boundary must have zero Lebesgue measure, restricting its applicability in advanced analysis.
Properties of Lebesgue Measure
Lebesgue measure extends Jordan measure by assigning values to a broader class of sets, including unbounded and highly irregular ones, ensuring countable additivity for disjoint sets. It is complete, meaning every subset of a null set is measurable, and invariant under translations and rotations in Euclidean space. These properties make Lebesgue measure fundamental in modern analysis and probability theory, surpassing Jordan measure's limitations which apply only to bounded sets with piecewise-smooth boundaries.
Applications in Real Analysis
Jordan measure is primarily used for simple sets with piecewise smooth boundaries, making it suitable for classical Riemann integration in real analysis. Lebesgue measure extends the concept to more complex and irregular sets, enabling integration of a wider class of functions, including those that are not Riemann integrable. This broader applicability of Lebesgue measure is fundamental in advanced topics like measure theory, functional analysis, and probability theory.
Summary and Comparative Table
Jordan measure applies to bounded sets with piecewise smooth boundaries, measuring volumes via outer approximations using finite unions of rectangles. Lebesgue measure extends this concept to more general sets, including those with intricate boundaries, capturing measure through countable unions of intervals and providing completeness by assigning measure zero to subsets of null sets. The comparative table highlights Jordan measure as limited to Jordan measurable sets and non-complete, while Lebesgue measure covers a wider class of measurable sets, is complete, and supports countable additivity, making it fundamental in modern analysis.
Jordan measure Infographic
 libterm.com
libterm.com