Analytic sets are a class of subsets in descriptive set theory characterized by being projections of Borel sets, and they play a crucial role in understanding measurable and definable properties within Polish spaces. These sets often exhibit complex structures that challenge classical measurability and definability concepts, making them central to advanced mathematical analysis. Explore the rest of this article to deepen your understanding of analytic sets and their significance in logic and topology.
Table of Comparison
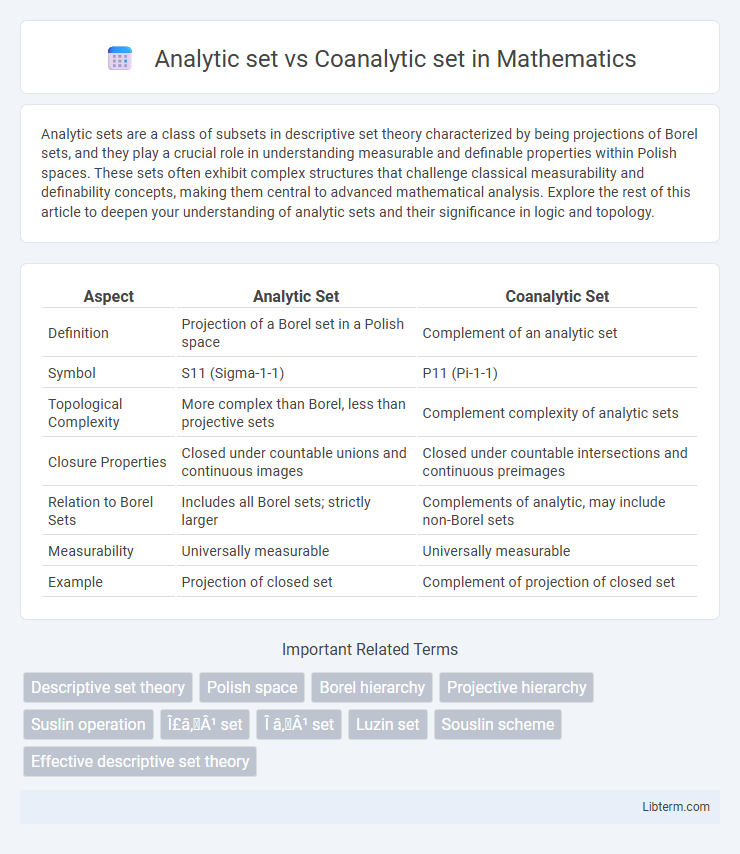
| Aspect | Analytic Set | Coanalytic Set |
|---|---|---|
| Definition | Projection of a Borel set in a Polish space | Complement of an analytic set |
| Symbol | S11 (Sigma-1-1) | P11 (Pi-1-1) |
| Topological Complexity | More complex than Borel, less than projective sets | Complement complexity of analytic sets |
| Closure Properties | Closed under countable unions and continuous images | Closed under countable intersections and continuous preimages |
| Relation to Borel Sets | Includes all Borel sets; strictly larger | Complements of analytic, may include non-Borel sets |
| Measurability | Universally measurable | Universally measurable |
| Example | Projection of closed set | Complement of projection of closed set |
Introduction to Analytic and Coanalytic Sets
Analytic sets, also known as S11 sets, are projections of Borel sets in a Polish space and are fundamental objects in descriptive set theory due to their definability and structural properties. Coanalytic sets, or P11 sets, are complements of analytic sets and frequently arise in the study of complex hierarchical classifications of sets beyond the Borel hierarchy. Understanding the interaction between analytic and coanalytic sets is crucial for exploring the Wadge hierarchy and determinacy principles within the realm of effective descriptive set theory.
Historical Background and Significance
Analytic sets, introduced by descriptive set theorists such as Luzin and Sierpinski in the early 20th century, originated from efforts to extend the study of Borel sets while maintaining projective measurability. Coanalytic sets, defined as complements of analytic sets within Polish spaces, emerged as critical objects in understanding the structure and classification of definable sets beyond the Borel hierarchy. Their historical significance lies in foundational advances to descriptive set theory, impacting fields like measure theory, determinacy, and effective descriptive set theory.
Fundamental Definitions
Analytic sets, also known as S11 sets, are projections of Borel sets in a Polish space and play a crucial role in descriptive set theory due to their definability via continuous images of Borel sets. Coanalytic sets, also called P11 sets, are complements of analytic sets and are characterized by their complexity as sets not representable as projections of any Borel set. These fundamental definitions establish a hierarchy in the projective sets, underpinning many results in effective descriptive set theory and providing a framework for studying definability and classification problems in topological spaces.
Properties of Analytic Sets
Analytic sets, defined as continuous images of Borel sets in Polish spaces, possess key properties such as being universally measurable and having the property of Baire. They are closed under countable unions and intersections, and their complements form the class of coanalytic sets, which are complements of analytic sets. Analytic sets also exhibit the perfect set property in Polish spaces, ensuring that uncountable analytic sets contain a perfect subset.
Properties of Coanalytic Sets
Coanalytic sets, also known as P1^1 sets, are complements of analytic sets and exhibit closure under countable intersections and continuous preimages. They are typically not Borel but have a definable structure characterized by their relationship to projections of closed sets in Polish spaces. Coanalytic sets are crucial in descriptive set theory due to their complexity and role in hierarchy and determinacy results.
Key Differences Between Analytic and Coanalytic Sets
Analytic sets, also known as S11 sets, are projections of Borel sets in Polish spaces and are closed under continuous images and countable unions, while coanalytic sets, or P11 sets, are complements of analytic sets and are closed under countable intersections. Analytic sets may not be Borel, exhibiting higher descriptive complexity, whereas coanalytic sets often represent complements of these complex structures, highlighting their duality in descriptive set theory. Key distinctions include closure properties, definability through projections versus complements, and their roles in the projective hierarchy within Polish spaces.
Examples Illustrating Analytic and Coanalytic Sets
Analytic sets, such as projections of Borel sets in Polish spaces, include the classical example of the set of all irrational numbers in the real line, which can be represented as the continuous image of a perfect set. Coanalytic sets, being complements of analytic sets, include complex sets like the set of well-orderings on the natural numbers, which is coanalytic but not Borel. These examples illustrate the intricate hierarchy of definability and complexity within descriptive set theory, highlighting how analytic sets arise from projections while coanalytic sets come from complements, often involving subtle constructions beyond elementary Borel structure.
Descriptive Set Theory: Context and Applications
Analytic sets, defined as continuous images of Borel sets, form a fundamental class in descriptive set theory, characterized by their projective definability and closure under continuous mappings. Coanalytic sets, complements of analytic sets, often present higher complexity and are essential in studying hierarchies such as the projective hierarchy within Polish spaces. Applications in descriptive set theory include classifying complexity of definable sets, analyzing regularity properties, and resolving problems in logic, topology, and real analysis.
The Projective Hierarchy and Its Relevance
Analytic sets (S11) and coanalytic sets (P11) constitute the first level of the projective hierarchy, a fundamental framework in descriptive set theory for classifying complex sets of reals. Analytic sets are projections of Borel sets, while coanalytic sets are complements of analytic sets, both crucial in understanding definability beyond Borel hierarchy. The projective hierarchy extends through alternating projections and complements, with analytic and coanalytic sets serving as building blocks for higher-level complexities and applications in areas such as measure theory, effective descriptive set theory, and determinacy principles.
Open Problems and Current Research Directions
Analytic sets, defined as continuous images of Borel sets, and their complements, coanalytic sets, remain central to descriptive set theory with unresolved questions about their exact structural properties within projective hierarchies. Current research explores the fine interplay between determinacy axioms and regularity properties such as measurability, Baire category, and uniformization problems for analytic and coanalytic sets. Open problems also include characterizing their structural complexity in terms of definability, reducibility, and potential generalizations under large cardinal assumptions.
Analytic set Infographic
 libterm.com
libterm.com