A homeomorphic relationship describes a continuous, bijective mapping between two topological spaces that preserves their essential structure. This concept is crucial in fields such as mathematics and computer science for understanding how shapes and spaces can be transformed without altering their fundamental properties. Explore the article to uncover how homeomorphic mappings influence various scientific and practical applications.
Table of Comparison
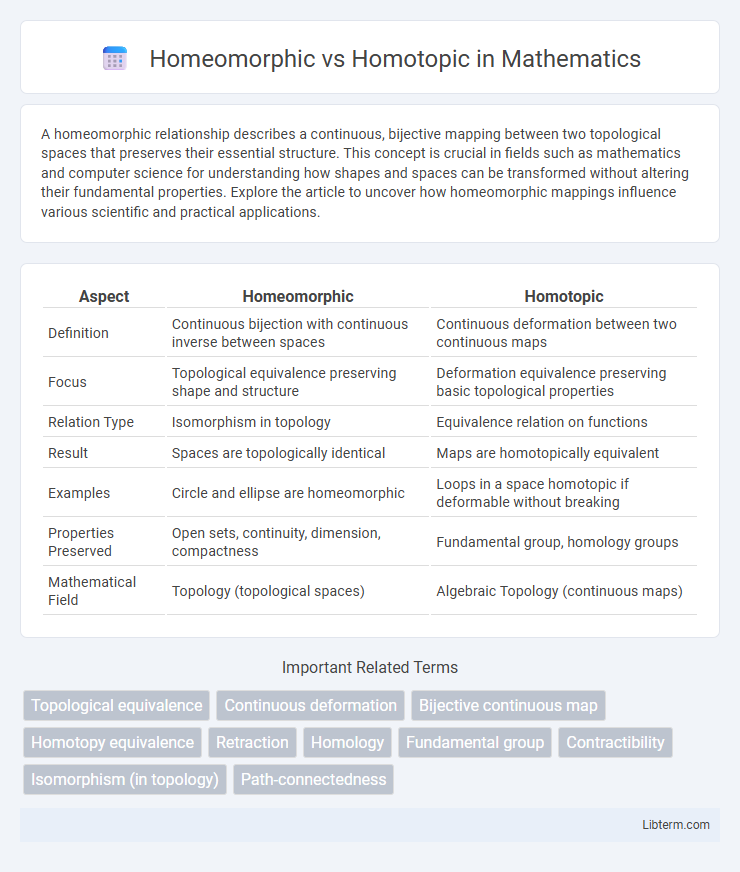
| Aspect | Homeomorphic | Homotopic |
|---|---|---|
| Definition | Continuous bijection with continuous inverse between spaces | Continuous deformation between two continuous maps |
| Focus | Topological equivalence preserving shape and structure | Deformation equivalence preserving basic topological properties |
| Relation Type | Isomorphism in topology | Equivalence relation on functions |
| Result | Spaces are topologically identical | Maps are homotopically equivalent |
| Examples | Circle and ellipse are homeomorphic | Loops in a space homotopic if deformable without breaking |
| Properties Preserved | Open sets, continuity, dimension, compactness | Fundamental group, homology groups |
| Mathematical Field | Topology (topological spaces) | Algebraic Topology (continuous maps) |
Introduction to Topological Concepts
Homeomorphic and homotopic are fundamental concepts in topology that describe different types of equivalences between spaces. Homeomorphic spaces are topologically identical, meaning there exists a continuous, bijective map with a continuous inverse between them, preserving all topological properties. Homotopic spaces are related by continuous deformations called homotopies, allowing one space to be continuously transformed into another without tearing or gluing, emphasizing the preservation of topological features up to continuous deformation rather than exact shape.
Defining Homeomorphic Spaces
Homeomorphic spaces are topological spaces that can be continuously transformed into each other through a bijective continuous function with a continuous inverse, preserving their topological properties. Defining homeomorphic spaces involves identifying a homeomorphism that illustrates this equivalence, ensuring both spaces share the same structure and are topologically indistinguishable. This concept is fundamental in topology to classify spaces based on shape rather than size or distortion.
Understanding Homotopic Maps
Homotopic maps refer to continuous functions between topological spaces that can be continuously deformed into each other, preserving their essential structural properties without necessarily being identical. Unlike homeomorphic maps, which establish a one-to-one, onto, and bicontinuous correspondence preserving exact topological equivalence, homotopic maps emphasize the concept of deformation through homotopy equivalence. Understanding homotopic maps involves analyzing continuous transformations within homotopy classes, crucial for studying algebraic topology and classifying spaces based on their intrinsic shape rather than precise form.
Key Differences: Homeomorphism vs Homotopy
Homeomorphism is a continuous bijection between topological spaces with a continuous inverse, preserving topological properties and indicating that two spaces are topologically equivalent. Homotopy involves a continuous deformation from one function or space to another, capturing the idea of spaces being "the same" up to continuous transformations but not necessarily identical in topological structure. Key differences include homeomorphism requiring a strict structural equivalence, while homotopy emphasizes equivalence up to deformation, making homotopic spaces weaker invariants in topology compared to homeomorphic ones.
Examples of Homeomorphic Spaces
Homeomorphic spaces are topologically equivalent, meaning there exists a continuous, bijective map with a continuous inverse between them, exemplified by a coffee cup and a doughnut, both having one hole. Other examples include a solid disk and a square, which can be continuously deformed into each other without cutting or gluing. Such spaces preserve properties like connectedness and compactness, illustrating the concept of topological equivalence.
Examples of Homotopic Transformations
Homotopic transformations include continuously deforming a coffee cup into a donut shape, as both share a single hole, illustrating their homotopy equivalence in topology. Another example involves shrinking a loop on a plane to a point without tearing or gluing, demonstrating a homotopy between the loop and the trivial path. These examples highlight how homotopic maps preserve topological properties while allowing flexible continuous deformations.
Topological Invariants and Their Role
Topological invariants such as the fundamental group, homology groups, and Euler characteristic play a crucial role in distinguishing homeomorphic and homotopic spaces. Homeomorphic spaces preserve all topological invariants exactly, indicating a strong form of equivalence, while homotopic spaces may share some invariants like homotopy type but differ in finer structures. Understanding these invariants helps classify spaces by revealing properties that remain unchanged under continuous deformations versus those requiring stronger equivalences.
Applications in Mathematics and Science
Homeomorphic structures enable topological classification of spaces by preserving properties like connectedness and compactness, essential in fields such as geometry and data analysis. Homotopic equivalence is crucial in algebraic topology for studying continuous deformations, influencing applications in robotics path planning and sensor network coverage. Both concepts facilitate understanding spatial properties and transformations, underpinning advanced research in mathematical physics and computer science.
Common Misconceptions and Pitfalls
Homeomorphic spaces are topologically identical with a continuous bijection and continuous inverse, while homotopic maps refer to continuous deformations between functions within a space. A common misconception is treating homotopy equivalence as a stronger condition than homeomorphism, although homeomorphism implies homotopy equivalence but not vice versa. Pitfalls arise when ignoring that homotopy preserves only the fundamental shape or connectivity, not exact geometric or topological structure, leading to errors in classifying spaces.
Conclusion: Choosing Between Homeomorphism and Homotopy
Choosing between homeomorphism and homotopy depends on the desired level of equivalence in topological spaces. Homeomorphism requires a bijective, continuous map with a continuous inverse, preserving all topological properties and structure intact, suitable for classifying spaces that are topologically identical. Homotopy provides a more flexible equivalence by allowing continuous deformation between maps, capturing essential shape features while ignoring finer geometric details, making it ideal for studying spaces up to deformation.
Homeomorphic Infographic
 libterm.com
libterm.com