Closed category words consist of functional words such as prepositions, conjunctions, articles, and pronouns that rarely accept new additions, maintaining the structural integrity of language. These essential words serve as grammatical connectors and provide relationships between content words, enhancing the clarity and coherence of your sentences. Dive deeper into this article to explore how closed category words shape effective communication and language learning.
Table of Comparison
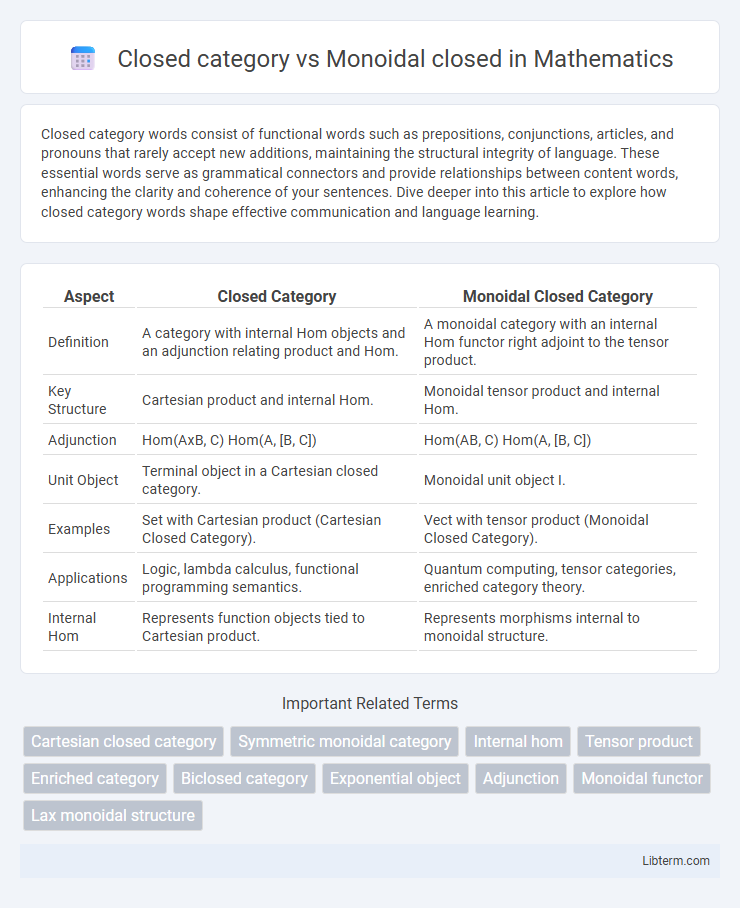
| Aspect | Closed Category | Monoidal Closed Category |
|---|---|---|
| Definition | A category with internal Hom objects and an adjunction relating product and Hom. | A monoidal category with an internal Hom functor right adjoint to the tensor product. |
| Key Structure | Cartesian product and internal Hom. | Monoidal tensor product and internal Hom. |
| Adjunction | Hom(AxB, C) Hom(A, [B, C]) | Hom(AB, C) Hom(A, [B, C]) |
| Unit Object | Terminal object in a Cartesian closed category. | Monoidal unit object I. |
| Examples | Set with Cartesian product (Cartesian Closed Category). | Vect with tensor product (Monoidal Closed Category). |
| Applications | Logic, lambda calculus, functional programming semantics. | Quantum computing, tensor categories, enriched category theory. |
| Internal Hom | Represents function objects tied to Cartesian product. | Represents morphisms internal to monoidal structure. |
Introduction to Closed Categories and Monoidal Closed Categories
Closed categories feature internal hom-functors that provide a way to represent morphisms as objects, enabling function type constructions within the category. Monoidal closed categories extend this concept by introducing a tensor product with an internal hom-functor that is adjoint to the tensor, enriching the structure with both monoidal and closed properties. These frameworks are fundamental in categorical logic and programming language semantics, facilitating the modeling of function spaces and tensorial interactions in a unified algebraic setting.
Defining Closed Categories
Closed categories are foundational structures in category theory where each hom-functor has a right adjoint, enabling the internalization of morphisms as objects, characterized by an internal hom-functor. Monoidal closed categories extend this concept to monoidal categories, having an internal hom-functor relative to the monoidal product, allowing the expression of morphisms compatible with the tensor structure. The defining feature of closed categories is the existence of exponential objects or internal homs that represent morphisms internally, facilitating enriched categorical analysis and functional abstraction.
Understanding Monoidal Closed Categories
Monoidal closed categories extend the concept of closed categories by incorporating a tensor product with an internal hom-functor that satisfies a natural isomorphism Y^(X-) (Y^X)(-). This structure allows for a deep understanding of function spaces within a monoidal context, bridging category theory with linear logic and enriched category theory. Recognizing the internal hom as an adjoint functor to the tensor product is key to unraveling the richness of monoidal closed categories and their applications in theoretical computer science and algebra.
Key Differences Between Closed and Monoidal Closed Categories
Closed categories provide an internal hom-functor enabling function objects within the category, allowing morphisms to be represented as objects. Monoidal closed categories extend this concept by integrating a monoidal structure, offering a tensor product alongside an internal hom-functor compatible with the tensor. The key difference lies in the monoidal closed category's enhanced framework that combines monoidal and closed properties, facilitating richer constructions such as currying and evaluation in the presence of tensor products.
Internal Homs in Closed and Monoidal Closed Contexts
Internal Homs in closed categories provide an object representing morphisms between two objects, allowing function spaces within the category itself. Monoidal closed categories extend this concept by combining a tensor product structure with internal Homs, enabling the representation of morphisms in a context enriched by the monoidal operation. This tensor-Hom adjunction underpins the internal Hom's role in monoidal closed categories, facilitating enriched categorical constructions and higher-order mappings.
Semantics and Categorical Structures
Closed categories provide a framework where hom-objects exist internally, enabling function spaces to be objects within the category, which supports internal hom-functors essential for semantic interpretations in categorical structures. Monoidal closed categories extend this concept by incorporating a monoidal tensor product alongside an internal Hom, allowing the modeling of resource-sensitive semantics and enriching the expressiveness of categorical semantics with tensorial operations. The distinction is pivotal in semantics since closed categories emphasize internalizing morphisms, while monoidal closed categories unify this with monoidal structures, facilitating advanced semantic frameworks like linear logic and enriched category theory.
Examples of Closed Categories
Closed categories include cartesian closed categories like the category of sets (Set), where the exponential object represents function spaces. Monoidal closed categories, such as the category of vector spaces with the tensor product, provide an internal hom functor compatible with the monoidal structure. Examples of closed categories therefore illustrate how internal hom-objects generalize function spaces in various categorical contexts.
Examples of Monoidal Closed Categories
Monoidal closed categories exemplify structures where each object has an internal hom-functor adjoint to the tensor product, such as the category of vector spaces over a field with the tensor product and Hom-functor representing linear maps. Another key example is the category of topological spaces with the smash product and function space construction, enabling a closed monoidal structure relevant in algebraic topology. Cartesian closed categories, a special case of monoidal closed categories with the cartesian product, include sets with function spaces, highlighting the versatility of monoidal closure in categorical frameworks.
Applications in Logic and Computer Science
Closed categories provide a foundational framework for modeling function spaces and internal hom-objects, crucial in the semantics of typed lambda calculus and functional programming languages. Monoidal closed categories extend this structure by incorporating a tensor product, enabling the representation of resource-sensitive logics such as linear logic and applications in quantum computing. These categorical structures facilitate reasoning about computation, type systems, and program equivalences through their well-defined morphisms and internal hom-functors.
Summary: Choosing the Right Category Structure
Closed categories provide a framework where each hom-set can be represented internally, enabling function spaces as objects within the category. Monoidal closed categories extend this by integrating a tensor product with an internal hom-functor that satisfies specific adjunction properties, crucial for modeling processes like resource-sensitive computation. Selecting between closed and monoidal closed categories depends on the presence of a tensor structure and the need for internal hom-objects compatible with that tensor, guiding applications in logic, computer science, and categorical algebra.
Closed category Infographic
 libterm.com
libterm.com