Finite resources are limited and require careful management to ensure sustainability and long-term availability. Understanding how to optimize the use of finite assets can significantly impact your efficiency and environmental footprint. Explore the rest of this article to learn practical strategies for maximizing the value of finite resources.
Table of Comparison
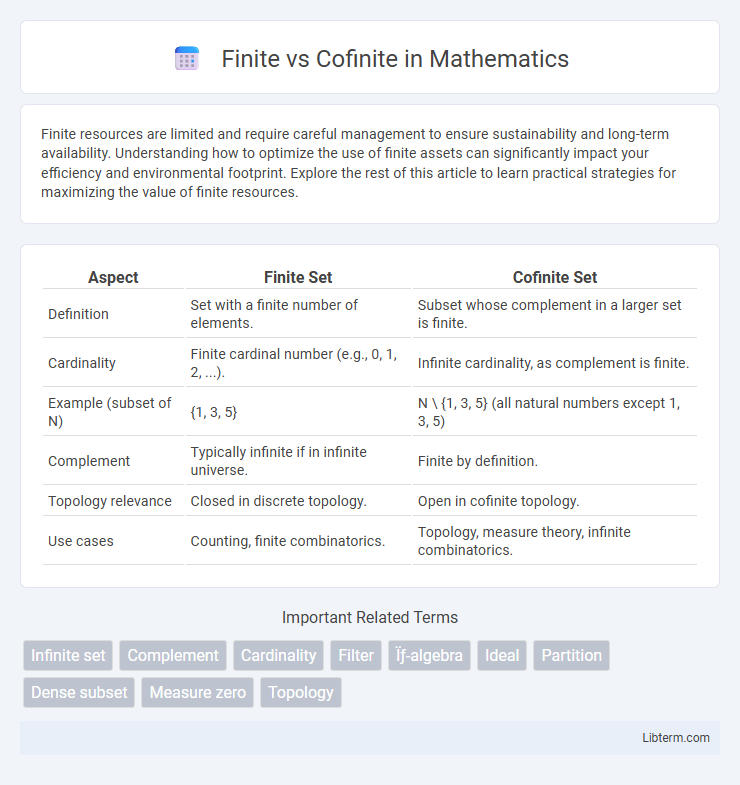
| Aspect | Finite Set | Cofinite Set |
|---|---|---|
| Definition | Set with a finite number of elements. | Subset whose complement in a larger set is finite. |
| Cardinality | Finite cardinal number (e.g., 0, 1, 2, ...). | Infinite cardinality, as complement is finite. |
| Example (subset of N) | {1, 3, 5} | N \ {1, 3, 5} (all natural numbers except 1, 3, 5) |
| Complement | Typically infinite if in infinite universe. | Finite by definition. |
| Topology relevance | Closed in discrete topology. | Open in cofinite topology. |
| Use cases | Counting, finite combinatorics. | Topology, measure theory, infinite combinatorics. |
Introduction to Finite and Cofinite Sets
Finite sets contain a limited number of elements, making them countable and easily enumerable, as seen in sets like {1, 2, 3}. Cofinite sets, by contrast, have complements that are finite, meaning the set itself can be infinite, but only a finite number of elements are excluded from the universal set. Understanding finite and cofinite sets is fundamental in topology and set theory, especially in analyzing properties related to closure and density.
Definitions: Finite Sets Explained
Finite sets are collections containing a limited number of elements, where each member can be explicitly counted or listed, such as {1, 2, 3}. Cofinite sets are subsets of a universal set whose complements are finite, meaning they include all but finitely many elements from the universal set. Understanding the distinction between finite and cofinite sets is crucial in fields like topology and set theory, where these concepts influence the structure and properties of different mathematical spaces.
Understanding Cofinite Sets
Cofinite sets are subsets of a given set whose complements are finite, meaning the set contains all but a limited number of elements from the original. Understanding cofinite sets involves recognizing their importance in topology and analysis, where they often form key examples of open or dense sets. Their properties contrast with finite sets by emphasizing the dominance of the large, nearly complete portion of the set rather than the small exceptions.
Key Differences Between Finite and Cofinite
Finite sets contain a limited number of elements, while cofinite sets are characterized by having complements that are finite within a larger universal set. The key difference lies in the nature of their complements: a finite set's complement can be infinite, whereas a cofinite set's complement is always finite. This distinction impacts set operations and is crucial in areas such as topology and logic.
Properties of Finite Sets
Finite sets are characterized by a specific number of distinct elements, enabling precise cardinality measurement. Their subsets are also finite, and operations such as union, intersection, and complement preserve finiteness or co-finiteness under defined conditions. Finite sets serve as a fundamental concept in combinatorics, discrete mathematics, and computer science due to their well-defined structure and predictability.
Properties of Cofinite Sets
Cofinite sets are subsets of a given universal set whose complements are finite, making them significant in topology and set theory due to their closure properties under finite intersections and unions. These sets are always infinite unless the universal set itself is finite, and any cofinite set contains all but finitely many elements of the universal set. Important properties include that the family of cofinite sets forms a filter, is closed under supersets, and their complements provide key examples in defining cofinite topologies.
Examples of Finite and Cofinite Sets
Finite sets include examples like {1, 2, 3}, {a, b, c}, and the empty set , each containing a limited number of elements. Cofinite sets are complements of finite sets within a universal set, such as the set of all natural numbers except {1, 2, 3}, denoted N \ {1, 2, 3}, which contains all natural numbers except those three. Understanding these examples clarifies the distinction: finite sets have a countable number of elements, while cofinite sets have elements missing only finitely many points from an infinite universal set.
Finite and Cofinite in Set Theory
In set theory, a finite set contains a limited number of elements, making it countable and easy to enumerate. A cofinite set is defined as the complement of a finite set within a given universal set, meaning it includes all elements except for a finite number of them. Understanding these concepts is crucial for applications in topology, measure theory, and combinatorics, where properties of sets and their complements influence structure and behavior.
Applications in Mathematics and Logic
Finite and cofinite sets play crucial roles in mathematics and logic, particularly in set theory and computational complexity. Finite sets are essential in combinatorics for counting problems, while cofinite sets, whose complements are finite, are significant in topology and model theory for understanding closure properties and definability. In logic, cofinite sets often appear in the study of decidability and the characterization of certain types of languages or theories.
Conclusion: Finite vs Cofinite Summary
Finite sets contain a limited number of elements, whereas cofinite sets have complements that are finite, meaning they include almost all elements of a given universal set except for a finite subset. The distinction is crucial in topology and set theory, where finite sets are closed and discrete, and cofinite sets form a cofinite topology that influences convergence and continuity properties. Understanding finite versus cofinite subsets helps clarify structural relationships in infinite sets and the behavior of functions defined on them.
Finite Infographic
 libterm.com
libterm.com