A Kahler manifold is a complex manifold equipped with a Hermitian metric whose associated 2-form is closed, providing a rich structure that intertwines complex, symplectic, and Riemannian geometry. This unique combination allows for powerful tools in both theoretical physics and differential geometry, particularly in fields like string theory and complex algebraic geometry. Discover how the properties of Kahler manifolds can enhance your understanding of advanced geometric concepts by reading the rest of the article.
Table of Comparison
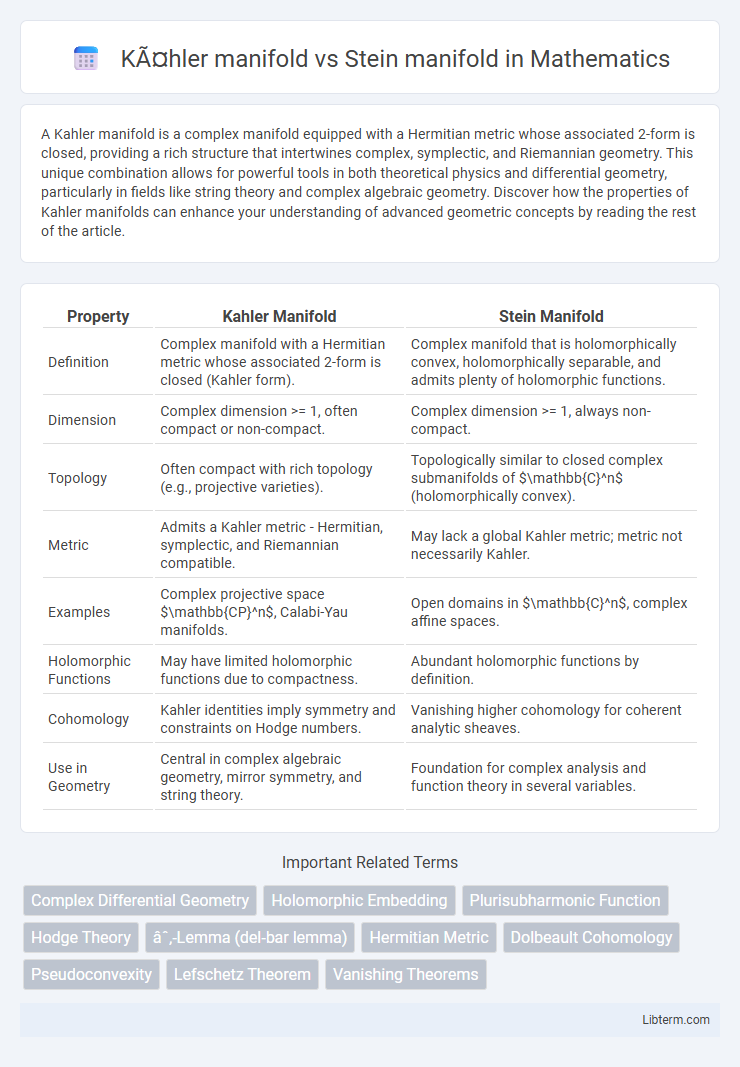
| Property | Kahler Manifold | Stein Manifold |
|---|---|---|
| Definition | Complex manifold with a Hermitian metric whose associated 2-form is closed (Kahler form). | Complex manifold that is holomorphically convex, holomorphically separable, and admits plenty of holomorphic functions. |
| Dimension | Complex dimension >= 1, often compact or non-compact. | Complex dimension >= 1, always non-compact. |
| Topology | Often compact with rich topology (e.g., projective varieties). | Topologically similar to closed complex submanifolds of $\mathbb{C}^n$ (holomorphically convex). |
| Metric | Admits a Kahler metric - Hermitian, symplectic, and Riemannian compatible. | May lack a global Kahler metric; metric not necessarily Kahler. |
| Examples | Complex projective space $\mathbb{CP}^n$, Calabi-Yau manifolds. | Open domains in $\mathbb{C}^n$, complex affine spaces. |
| Holomorphic Functions | May have limited holomorphic functions due to compactness. | Abundant holomorphic functions by definition. |
| Cohomology | Kahler identities imply symmetry and constraints on Hodge numbers. | Vanishing higher cohomology for coherent analytic sheaves. |
| Use in Geometry | Central in complex algebraic geometry, mirror symmetry, and string theory. | Foundation for complex analysis and function theory in several variables. |
Introduction to Kähler and Stein Manifolds
Kahler manifolds are complex manifolds equipped with a Hermitian metric whose associated two-form is closed, providing a rich interplay between complex geometry, symplectic structure, and Riemannian geometry. Stein manifolds, on the other hand, are complex manifolds characterized by holomorphic convexity and the existence of plenty of holomorphic functions, resembling affine complex spaces. These foundational structures play crucial roles in complex analysis and differential geometry, with Kahler manifolds serving as natural settings for Hodge theory, while Stein manifolds facilitate complex analytic methods and embedding problems.
Historical Context and Origins
Kahler manifolds originated from the work of Erich Kahler in the 1930s, who introduced a rich structure combining Riemannian, symplectic, and complex geometry, significantly advancing the study of complex manifolds with a metric compatible with both symplectic and complex structures. Stein manifolds trace back to Karl Stein's research in the 1950s, focusing on complex analysis and holomorphic functions, characterizing spaces that generalize domains of holomorphy in several complex variables. Both concepts emerged from distinct mathematical problems: Kahler manifolds address geometric structures bridging multiple fields, while Stein manifolds emphasize analytic properties fundamental to complex function theory.
Definitions: Kähler Manifolds
Kahler manifolds are complex manifolds equipped with a Hermitian metric whose associated 2-form is closed, making it symplectic and compatible with the complex structure. This structure combines Riemannian, complex, and symplectic geometry, characterized by a positive definite Kahler form derived from the metric and complex structure. In contrast, Stein manifolds are complex manifolds analogous to affine spaces in algebraic geometry, defined by holomorphic convexity and the existence of plenty of global holomorphic functions.
Definitions: Stein Manifolds
Stein manifolds are complex manifolds that are holomorphically convex and holomorphically separable, serving as the complex-analytic analogs of affine varieties in algebraic geometry. They admit proper holomorphic embeddings into complex Euclidean space, characterized by the existence of sufficiently many global holomorphic functions to separate points and provide local coordinates. These properties distinguish Stein manifolds from Kahler manifolds, which are equipped with a Hermitian metric whose associated (1,1)-form is closed, emphasizing geometric structures rather than holomorphic convexity.
Key Properties and Structures
Kahler manifolds exhibit a rich geometric structure characterized by a Hermitian metric compatible with a symplectic form, allowing for Hodge theory and complex differential geometry applications. Stein manifolds, as holomorphically convex complex manifolds, support the existence of plenty of global holomorphic functions, enabling powerful embedding theorems and function theory analogous to affine varieties. While Kahler manifolds emphasize metric and curvature properties critical in complex geometry and algebraic geometry, Stein manifolds focus on complex-analytic properties facilitating function theory and complex analysis.
Similarities Between Kähler and Stein Manifolds
Kahler and Stein manifolds both exhibit rich complex structures integral to complex geometry, with Kahler manifolds characterized by a Hermitian metric whose associated two-form is closed, and Stein manifolds defined by holomorphic convexity and separability. Both types of manifolds support holomorphic functions with strong analytical properties, facilitating complex analysis and algebraic geometry applications. Their shared capacity for defining plurisubharmonic functions highlights fundamental parallels in potential theory and complex differential geometry.
Fundamental Differences and Contrasts
Kahler manifolds are complex manifolds equipped with a Hermitian metric whose associated (1,1)-form is closed, yielding rich geometric structures such as Ricci curvature and Hodge theory. Stein manifolds, as complex analytic analogs of affine spaces, are holomorphically convex, holomorphically separable, and admit plenty of holomorphic functions, but lack the intrinsic metric structures of Kahler manifolds. The fundamental contrast lies in Kahler manifolds emphasizing geometric and metric properties with a symplectic form, while Stein manifolds focus on complex analytic properties and function theory without requiring closedness of the fundamental form or compactness conditions.
Examples of Kähler and Stein Manifolds
Compact complex projective spaces, such as complex projective space \(\mathbb{CP}^n\), serve as fundamental examples of Kahler manifolds due to their rich symplectic and complex structures. Stein manifolds are exemplified by domains of holomorphy in \(\mathbb{C}^n\), including open subsets like the unit ball or polydiscs, characterized by their holomorphic convexity and existence of plurisubharmonic exhaustion functions. Unlike Kahler manifolds, which are often compact and equipped with a Hermitian metric whose imaginary part is closed, Stein manifolds are typically non-compact and exhibit strong holomorphic convexity properties crucial for complex analysis and function theory.
Applications in Complex Geometry and Physics
Kahler manifolds play a crucial role in complex geometry and theoretical physics, particularly in string theory and supersymmetry, due to their rich structure combining symplectic, Riemannian, and complex geometry which enables the study of Calabi-Yau manifolds and mirror symmetry. Stein manifolds serve as fundamental examples of complex manifolds that admit proper holomorphic embeddings into complex Euclidean spaces, facilitating problems in several complex variables and complex dynamical systems. In physics, the geometric quantization on Kahler manifolds aids in formulating quantum field theories, while Stein manifolds provide the analytical framework for complex analytic methods in quantum mechanics and complex differential equations.
Open Problems and Research Directions
Kahler manifolds, characterized by their rich geometric structure combining symplectic, complex, and Riemannian properties, present open problems related to understanding their global classification and the existence of special metrics such as Kahler-Einstein metrics on non-compact manifolds. Stein manifolds, defined as complex manifolds that are holomorphically convex and resemble affine complex spaces, pose research challenges in embedding problems and their interaction with complex dynamical systems. Current research explores the boundaries between these classes, particularly the extension of Kahler structures on Stein manifolds and the impact of complex analytic properties on curvature and topological invariants.
Kähler manifold Infographic
 libterm.com
libterm.com