A pullback in mathematics refers to the operation of transferring structures such as functions, forms, or measures from one space to another via a mapping, preserving essential properties. Limits describe the value that a function or sequence approaches as the input or index approaches a particular point or infinity, fundamental in calculus and analysis. Explore the rest of this article to deepen your understanding of pullbacks, limits, and their pivotal roles in advanced mathematical concepts.
Table of Comparison
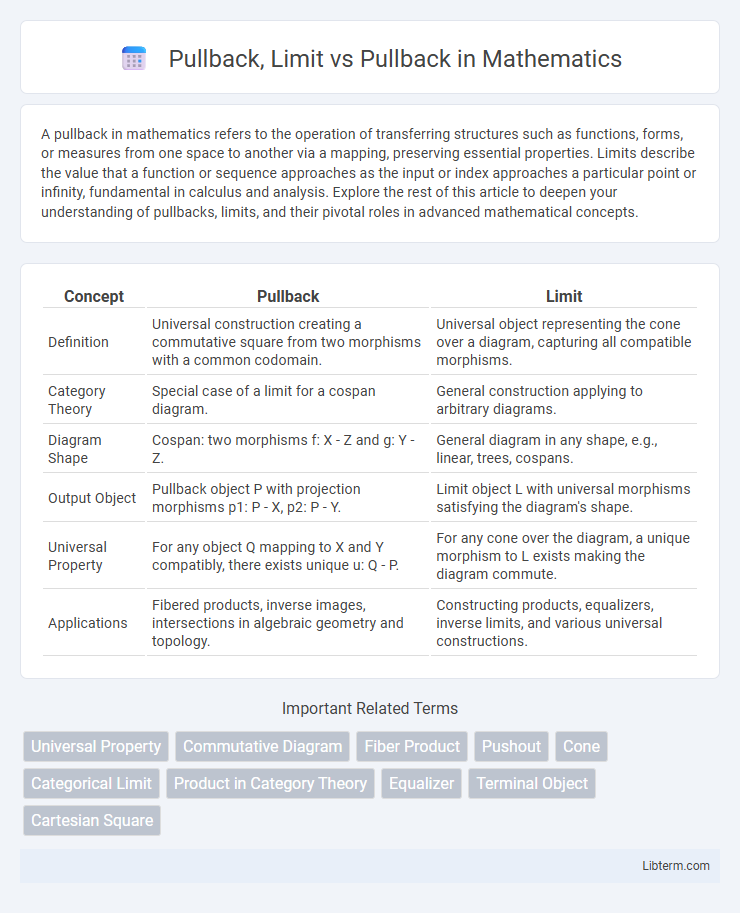
| Concept | Pullback | Limit |
|---|---|---|
| Definition | Universal construction creating a commutative square from two morphisms with a common codomain. | Universal object representing the cone over a diagram, capturing all compatible morphisms. |
| Category Theory | Special case of a limit for a cospan diagram. | General construction applying to arbitrary diagrams. |
| Diagram Shape | Cospan: two morphisms f: X - Z and g: Y - Z. | General diagram in any shape, e.g., linear, trees, cospans. |
| Output Object | Pullback object P with projection morphisms p1: P - X, p2: P - Y. | Limit object L with universal morphisms satisfying the diagram's shape. |
| Universal Property | For any object Q mapping to X and Y compatibly, there exists unique u: Q - P. | For any cone over the diagram, a unique morphism to L exists making the diagram commute. |
| Applications | Fibered products, inverse images, intersections in algebraic geometry and topology. | Constructing products, equalizers, inverse limits, and various universal constructions. |
Understanding Pullbacks in Category Theory
Pullbacks in category theory represent a universal construction that combines two morphisms with a common codomain to form a commutative square, capturing the notion of a fibered product. Limits generalize pullbacks by providing a universal cone over any given diagram, making pullbacks a specific case of limits involving span-shaped diagrams. Understanding pullbacks as particular limits aids in analyzing how objects and morphisms interact within categories, facilitating deeper insights into categorical constructions and their applications in algebra and topology.
Formal Definition of Pullback
A pullback in category theory is defined as a universal construction that represents the limit of a diagram consisting of two morphisms with a common codomain. Formally, given morphisms \( f: X \to Z \) and \( g: Y \to Z \), their pullback is an object \( P \) along with projections \( p_1: P \to X \) and \( p_2: P \to Y \) such that \( f \circ p_1 = g \circ p_2 \), satisfying the universal property that for any object \( Q \) with morphisms \( q_1: Q \to X \), \( q_2: Q \to Y \) where \( f \circ q_1 = g \circ q_2 \), there exists a unique morphism \( u: Q \to P \) making the diagram commute. This formal definition establishes the pullback as a special case of a limit, specifically the limit of the cospan diagram formed by \( f \) and \( g \).
Visualizing Pullbacks with Commutative Diagrams
A pullback in category theory is a limit of a diagram consisting of two morphisms with a shared codomain, representing the most universal object mapping into both domain objects with consistent compositions. Unlike general limits that can involve various shapes, the pullback specifically captures a fiber product or inverse image concept, making it a fundamental construction in categories such as sets, topological spaces, and schemes. Visualizing pullbacks with commutative diagrams highlights their universal property by showing a square where the two morphisms into a common codomain commute and any object mapping into the pullback factors uniquely through this square, emphasizing the pullback's role as the categorical limit of the given diagram.
Key Properties of Pullbacks
Pullbacks, also known as fibered products, are a fundamental construction in category theory capturing the universal property of "pulling back" along morphisms. The key properties of pullbacks include their ability to represent limits of diagrams shaped like two morphisms with a common codomain, ensuring uniqueness and universality up to unique isomorphism. Unlike general limits, pullbacks specifically provide a categorical notion of the intersection or fiber product, preserving structure through commutative squares and reflecting properties like monomorphisms or epimorphisms under suitable conditions.
Limit: A General Categorical Construction
Limits in category theory generalize constructions such as products, equalizers, and pullbacks by providing a universal cone over a diagram. A pullback is a specific example of a limit corresponding to the fiber product of two morphisms with a common codomain, capturing their universal property. Limits encapsulate the essence of universal constructions, allowing the characterization and comparison of diagrams through unique factorization properties in any category.
How Limits Relate to Pullbacks
Pullbacks are a specific type of limit in category theory, where the pullback of two morphisms f: X - Z and g: Y - Z is the limit of the diagram formed by these morphisms. Limits generalize pullbacks by encompassing cones over more complex diagrams, whereas pullbacks focus on the universal property related to a pair of morphisms sharing a codomain. Understanding pullbacks as limits clarifies their role in defining fibered products and properties such as universality and uniqueness within categories.
Pullback vs. Limit: Semantic Differences
Pullbacks and limits are fundamental concepts in category theory with distinct semantic roles. A pullback specifically represents a universal construction that models the product of two morphisms with a shared codomain, capturing the idea of a "fibered product" or "pulling back" along maps. Limits, on the other hand, generalize pullbacks by providing universal cones over arbitrary diagrams, making pullbacks a special case of limits focused on pairs of morphisms rather than complex diagram shapes.
Examples Illustrating Pullbacks and Limits
Pullbacks and limits are fundamental concepts in category theory, with pullbacks representing a specific type of limit that generalizes the notion of a fiber product. For example, given two morphisms \(f: X \to Z\) and \(g: Y \to Z\), their pullback is an object \(P\) together with projections \(p_1: P \to X\) and \(p_2: P \to Y\) such that \(f \circ p_1 = g \circ p_2\), often visualized as a commutative square. Limits encompass a broader class of universal constructions including products, equalizers, and pullbacks, whereby limits capture the "best fit" object mediating a diagram of morphisms, illustrated by the product limit of objects \(A\) and \(B\) with projections mapping into each summand.
Applications of Pullbacks in Mathematics
Pullbacks play a crucial role in category theory by providing a universal construction to "pull back" objects along morphisms, forming a commutative square that generalizes fiber products. Limits represent a broader concept, encapsulating cones and universal properties including pullbacks as specific instances useful for defining products, kernels, and equalizers. Applications of pullbacks in mathematics include algebraic geometry for defining fibered products of schemes, topology for constructing fiber bundles, and homological algebra for investigating exact sequences and derived functors.
Summary: Distinguishing Limit and Pullback
Limits in category theory represent universal cones aggregating a diagram's data into a cohesive object, ensuring unique factorization through it. Pullbacks, a specific type of limit involving two morphisms with a shared codomain, function as a universal solution to the problem of "pulling back" along these maps, constructing a fibered product. The distinction lies in pullbacks serving as specialized limits focused on the interaction and intersection of morphisms, whereas limits encapsulate a broader range of universal constructions across various diagram shapes.
Pullback, Limit Infographic
 libterm.com
libterm.com