Fiber products are essential in mathematics, particularly in category theory and algebraic geometry, where they represent a universal construction combining two objects over a shared base. Understanding fiber products helps you grasp how different structures interact and connect within various mathematical frameworks. Explore the rest of the article to discover detailed examples and applications of fiber products in diverse fields.
Table of Comparison
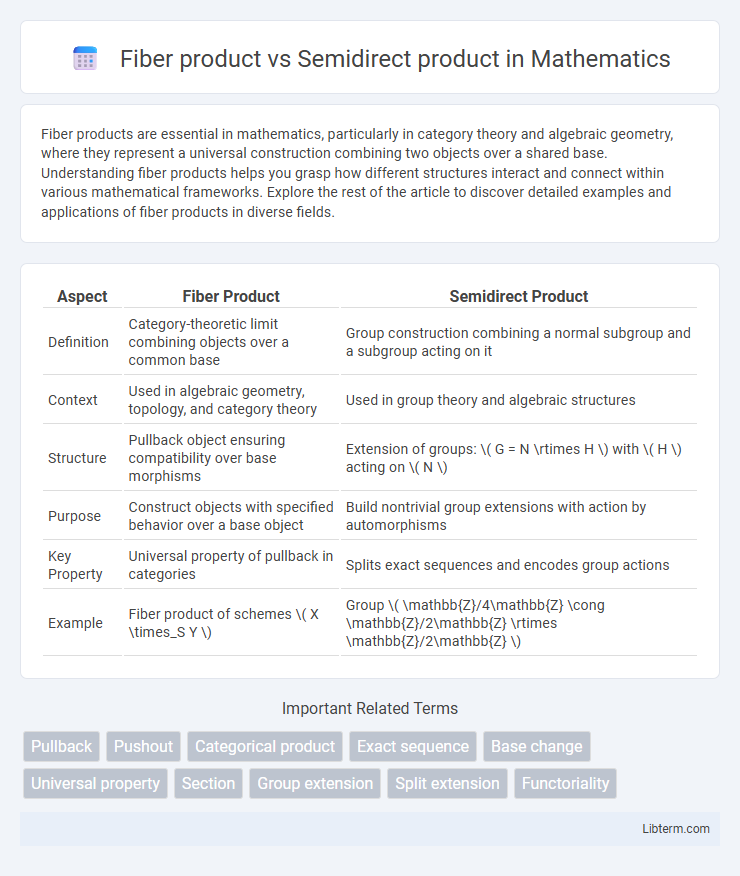
| Aspect | Fiber Product | Semidirect Product |
|---|---|---|
| Definition | Category-theoretic limit combining objects over a common base | Group construction combining a normal subgroup and a subgroup acting on it |
| Context | Used in algebraic geometry, topology, and category theory | Used in group theory and algebraic structures |
| Structure | Pullback object ensuring compatibility over base morphisms | Extension of groups: \( G = N \rtimes H \) with \( H \) acting on \( N \) |
| Purpose | Construct objects with specified behavior over a base object | Build nontrivial group extensions with action by automorphisms |
| Key Property | Universal property of pullback in categories | Splits exact sequences and encodes group actions |
| Example | Fiber product of schemes \( X \times_S Y \) | Group \( \mathbb{Z}/4\mathbb{Z} \cong \mathbb{Z}/2\mathbb{Z} \rtimes \mathbb{Z}/2\mathbb{Z} \) |
Introduction to Fiber and Semidirect Products
Fiber products combine objects over a common base, enabling the construction of new objects characterized by their projections aligning with given morphisms. Semidirect products describe a method to build a group from two subgroups, where one acts on the other, generalizing direct products by incorporating nontrivial group actions. Both constructions facilitate complex algebraic manipulations in categories and group theory, respectively, highlighting their importance in structural analysis.
Defining the Fiber Product in Algebra
The fiber product in algebra is defined as the pullback of two morphisms with a common codomain, forming an object that 'fibers' over this codomain by pairing elements mapped to the same target. Unlike the semidirect product, which constructs a group from a normal subgroup and a complementary subgroup with a specified action, the fiber product emphasizes universal properties and categorical limits. This construction is fundamental in algebraic geometry and category theory for gluing objects along shared structures and ensuring compatibility of mappings.
Understanding the Semidirect Product Structure
The semidirect product combines two groups \( N \) and \( H \) where \( N \) is normal, allowing \( H \) to act on \( N \) via automorphisms, forming a nontrivial group extension. Unlike the fiber product, which intersects groups over a common image, the semidirect product encodes a specific action that determines the multiplication structure within the product. Understanding this structure is crucial for analyzing group actions, symmetry groups, and constructing examples where direct product decompositions fail.
Key Differences Between Fiber and Semidirect Products
Fiber products combine objects in category theory by pulling back along morphisms to a common codomain, primarily focusing on universal properties and limits. Semidirect products form groups by combining a normal subgroup and a complementary subgroup with a specified action, emphasizing group structure and internal symmetries. The fiber product is defined via a universal property related to equalizing maps, whereas the semidirect product is a construction that encodes an action of one group on another within a single combined group.
Algebraic Properties and Use Cases
Fiber products in algebra combine objects over a common base, preserving pullbacks and ensuring universal properties critical in category theory and algebraic geometry. Semidirect products construct groups from a normal subgroup and a complementary subgroup with an action, capturing group extensions and non-abelian structures prominent in group theory and crystallography. Fiber products excel in gluing schemes and sheaves, while semidirect products model symmetries and automorphisms in algebraic and geometric contexts.
Examples of Fiber Products in Mathematics
Fiber products in mathematics often appear in algebraic geometry, where schemes are glued together over a base scheme, such as the fiber product of two affine schemes Spec(A) and Spec(B) over Spec(R) resulting in Spec(A _R B). Another example is in category theory, where fiber products represent pullbacks, like the fiber product of sets X and Y over a set Z with functions f: X - Z and g: Y - Z defined by {(x,y) in XxY | f(x) = g(y)}. This contrasts with semidirect products in group theory, which construct new groups by combining a normal subgroup and a subgroup acting on it, not involving universal pullback properties characteristic of fiber products.
Semidirect Products: Group Actions and Applications
Semidirect products arise from group actions where one group acts on another via automorphisms, allowing the construction of a new group that combines the structures of both. This product generalizes the direct product by incorporating nontrivial interaction between the factor groups, crucial in classifying group extensions and describing symmetry groups in various mathematical and physical contexts. Applications of semidirect products include crystallography, where they model space groups, and algebraic topology, where they aid in understanding fundamental groups with non-simple decompositions.
Advantages and Limitations of Each Product
Fiber products provide a powerful tool for constructing objects that satisfy universal properties in category theory, enabling precise pullbacks and fibered constructions essential for algebraic geometry and topology. Their advantage lies in creating subobjects defined by equalizing conditions, but they can be limited by complexity and lack of straightforward interpretation in general algebraic structures. Semidirect products excel in group theory by combining a normal subgroup and a complementary subgroup with a defined action, facilitating the study of group extensions and automorphisms, yet they require explicit action definitions and may not represent all possible group extensions.
Choosing Between Fiber and Semidirect Products
Choosing between a fiber product and a semidirect product depends on the categorical context and the algebraic structure involved; fiber products are utilized to construct pullbacks in categories, preserving universal properties and enabling limits, whereas semidirect products combine groups with a specified group action, capturing extensions where one subgroup acts on another. Fiber products maintain compatibility with morphisms over a base object, making them essential in topology and algebraic geometry, while semidirect products are pivotal in group theory for building nontrivial group extensions and analyzing symmetry operations. The decision hinges on whether the goal is to achieve a universal construction satisfying a pullback condition or to model group extensions through internal actions.
Conclusion: Which Product Suits Your Needs?
Fiber products excel in scenarios requiring the pullback construction to enforce compatibility between objects via shared morphisms, making them ideal for category theory and algebraic geometry applications. Semidirect products are favored in group theory and algebra for combining groups with a specified action, providing a flexible structure that incorporates both normal and complement subgroups. Choosing between fiber and semidirect products depends on whether your focus is on categorical pullbacks ensuring universal properties or on algebraic group actions combining distinct subgroup dynamics.
Fiber product Infographic
 libterm.com
libterm.com