The concept of an upper limit defines the maximum boundary or threshold that cannot be exceeded in various contexts, such as finance, physics, or technology. Understanding this limit helps optimize performance and avoid risks associated with overstepping established boundaries. Explore the article to discover how recognizing your upper limits can enhance decision-making and efficiency.
Table of Comparison
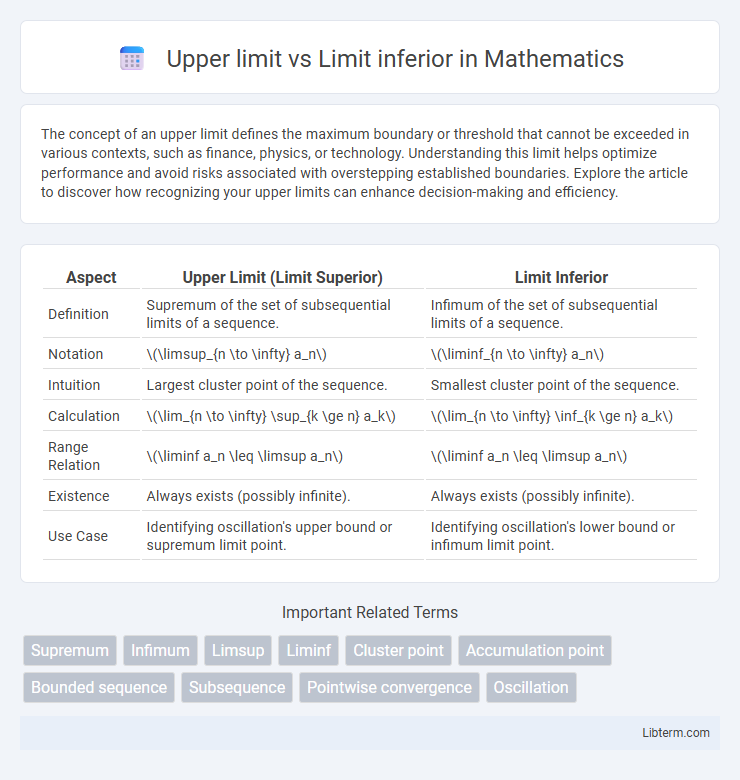
| Aspect | Upper Limit (Limit Superior) | Limit Inferior |
|---|---|---|
| Definition | Supremum of the set of subsequential limits of a sequence. | Infimum of the set of subsequential limits of a sequence. |
| Notation | \(\limsup_{n \to \infty} a_n\) | \(\liminf_{n \to \infty} a_n\) |
| Intuition | Largest cluster point of the sequence. | Smallest cluster point of the sequence. |
| Calculation | \(\lim_{n \to \infty} \sup_{k \ge n} a_k\) | \(\lim_{n \to \infty} \inf_{k \ge n} a_k\) |
| Range Relation | \(\liminf a_n \leq \limsup a_n\) | \(\liminf a_n \leq \limsup a_n\) |
| Existence | Always exists (possibly infinite). | Always exists (possibly infinite). |
| Use Case | Identifying oscillation's upper bound or supremum limit point. | Identifying oscillation's lower bound or infimum limit point. |
Introduction to Upper Limit and Limit Inferior
Upper limit and limit inferior are fundamental concepts in mathematical analysis used to describe the behavior of sequences. The upper limit, or lim sup, represents the greatest accumulation point or the largest subsequential limit of a sequence, capturing the maximum boundary the sequence approaches infinitely often. In contrast, limit inferior, or lim inf, denotes the smallest accumulation point or the minimal subsequential limit, reflecting the lowest boundary the sequence eventually stays above.
Defining the Concepts: Upper Limit vs Limit Inferior
The upper limit (lim sup) of a sequence is the supremum of its set of subsequential limits, representing the greatest accumulation point. The limit inferior (lim inf) is the infimum of the same set, indicating the smallest accumulation point. These concepts capture the boundary behavior of sequences, especially when convergence does not occur, providing precise bounds on the sequence's oscillations.
Mathematical Notation and Symbols
The upper limit, or limit superior, denoted as \(\limsup_{n \to \infty} a_n\), represents the supremum of the set of subsequential limits of a sequence \(\{a_n\}\), effectively capturing the largest cluster point. The limit inferior, symbolized by \(\liminf_{n \to \infty} a_n\), corresponds to the infimum of the set of subsequential limits, indicating the smallest value subsequences approach. These are formally defined using notation such as \(\limsup_{n \to \infty} a_n = \lim_{n \to \infty} \sup_{k \ge n} a_k\) and \(\liminf_{n \to \infty} a_n = \lim_{n \to \infty} \inf_{k \ge n} a_k\).
Visual Representation and Interpretation
The upper limit (lim sup) of a sequence visually represents the greatest accumulation point or the supremum of subsequential limits, often depicted as the highest horizontal line approached infinitely often by the sequence. The limit inferior (lim inf) corresponds to the lowest accumulation point or the infimum of subsequential limits, typically shown as the lowest horizontal boundary that the sequence values approach infinitely closely. In graphical terms, the region between the lim inf and lim sup bands encapsulates the range within which the sequence oscillates endlessly, providing insight into the sequence's long-term behavior and variations.
Calculating Upper Limit and Limit Inferior
Calculating the upper limit involves finding the supremum of the set of limit points or the least upper bound of the sequence's tail values. The limit inferior, or lim inf, is computed by taking the infimum of the set of limit points or the greatest lower bound of the sequence's tail values. Both calculations require analyzing subsequential limits to determine bounds that describe the sequence's long-term behavior.
Key Properties and Differences
The upper limit (lim sup) of a sequence represents the greatest limit point or the supremum of subsequential limits, while the limit inferior (lim inf) corresponds to the smallest limit point or the infimum of subsequential limits. Key properties include lim inf <= lim sup always, with equality holding if and only if the sequence converges. Unlike the limit inferior, which captures the long-term lower bounds of oscillations, the upper limit captures the long-term upper bounds, providing a nuanced description of the sequence's behavior at infinity.
Practical Examples in Sequences
The upper limit (lim sup) of a sequence represents the largest cluster point or the supremum of its tail subsequences, often illustrating the highest boundary that subsequences can approach, such as the sequence defined by a_n = (-1)^n(1 + 1/n) where lim sup equals 1. The limit inferior (lim inf) denotes the smallest cluster point or the infimum of the tail subsequences, capturing the lowest boundary limit, as demonstrated by the same sequence where lim inf equals -1. Practical examples include oscillating sequences like a_n = sin(n)/n where lim inf and lim sup both converge to zero, confirming that the sequence's extreme limit points coincide with its actual limit.
Upper Limit and Limit Inferior in Real Analysis
Upper limit (lim sup) of a sequence in real analysis captures the supremum of its subsequential limits, representing the largest cluster point or the limit of the sequence's tail supremums. Limit inferior (lim inf) denotes the infimum of all subsequential limits, reflecting the smallest limit point or the limit of the sequence's tail infimums. Both concepts are crucial in characterizing the asymptotic behavior of bounded sequences and determining convergence criteria.
Common Misconceptions
Upper limit (lim sup) and limit inferior (lim inf) are often misunderstood as simply the maximum and minimum of a sequence, but they actually represent the supremum of subsequential limits and the infimum of subsequential limits, respectively. A common misconception is treating them as limits of single values rather than bounds for the eventual behavior of a sequence, especially when the sequence does not converge. Correct interpretation requires recognizing lim sup as the greatest cluster point, while lim inf is the smallest cluster point, providing crucial insights into the sequence's oscillatory tendencies.
Applications in Mathematics and Beyond
Upper limit (lim sup) and limit inferior (lim inf) play crucial roles in real analysis, measure theory, and probability, providing bounds that describe the asymptotic behavior of sequences and functions. In stochastic processes, lim sup and lim inf help characterize almost sure convergence and oscillatory behavior, while in optimization, they assist in defining stability criteria and convergence thresholds. Beyond mathematics, these concepts find applications in economics for modeling upper and lower bounds of fluctuating markets and in computer science for analyzing algorithmic complexity limits and network performance bounds.
Upper limit Infographic
 libterm.com
libterm.com