Lambert series are infinite series used extensively in number theory and combinatorics, often represented as sums involving divisor functions and q-exponentials. These series reveal deep connections between arithmetic functions and modular forms, making them a powerful tool for analyzing integer partitions and generating functions. Explore this article to uncover how Lambert series can enhance your understanding of mathematical patterns and solve complex problems.
Table of Comparison
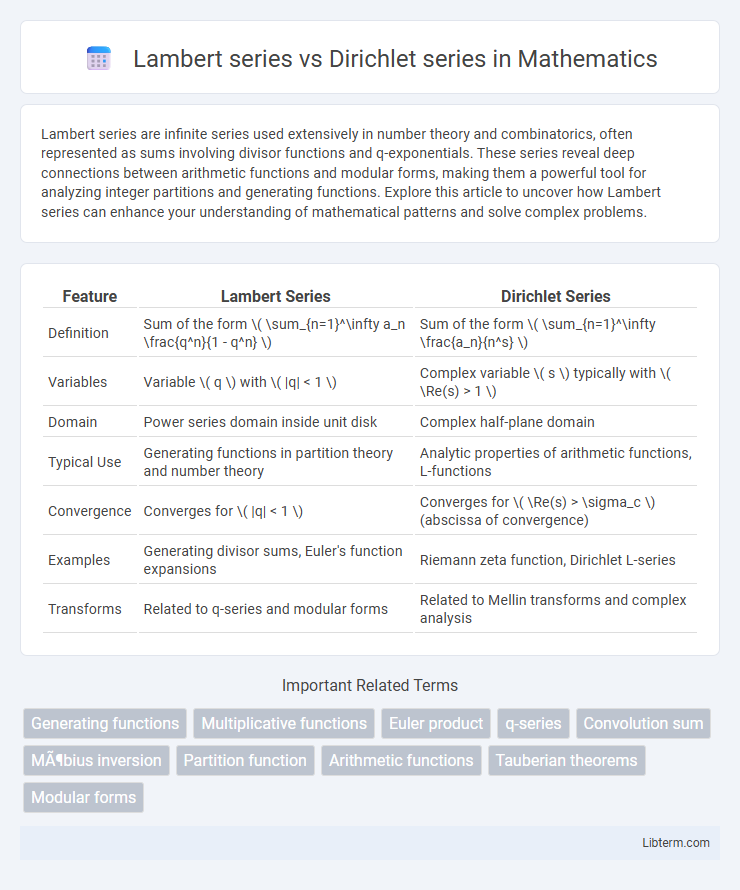
| Feature | Lambert Series | Dirichlet Series |
|---|---|---|
| Definition | Sum of the form \( \sum_{n=1}^\infty a_n \frac{q^n}{1 - q^n} \) | Sum of the form \( \sum_{n=1}^\infty \frac{a_n}{n^s} \) |
| Variables | Variable \( q \) with \( |q| < 1 \) | Complex variable \( s \) typically with \( \Re(s) > 1 \) |
| Domain | Power series domain inside unit disk | Complex half-plane domain |
| Typical Use | Generating functions in partition theory and number theory | Analytic properties of arithmetic functions, L-functions |
| Convergence | Converges for \( |q| < 1 \) | Converges for \( \Re(s) > \sigma_c \) (abscissa of convergence) |
| Examples | Generating divisor sums, Euler's function expansions | Riemann zeta function, Dirichlet L-series |
| Transforms | Related to q-series and modular forms | Related to Mellin transforms and complex analysis |
Introduction to Lambert and Dirichlet Series
Lambert series and Dirichlet series are fundamental tools in analytic number theory used to study arithmetic functions. A Lambert series is expressed as \(\sum_{n=1}^\infty a_n \frac{q^n}{1-q^n}\), often related to divisor sums and q-series expansions. Dirichlet series, defined as \(\sum_{n=1}^\infty \frac{a_n}{n^s}\), play a crucial role in the analysis of multiplicative functions and are central to the theory of the Riemann zeta function and L-functions.
Historical Development and Origin
Lambert series trace back to Johann Heinrich Lambert's 18th-century investigations into series involving divisor functions, playing a pivotal role in the development of analytic number theory. Dirichlet series emerged in the 19th century from Johann Peter Gustav Lejeune Dirichlet's work on L-functions and the distribution of prime numbers in arithmetic progressions. The historical progression from Lambert's investigations on q-series to Dirichlet's application of complex analysis established foundational tools for modern multiplicative number theory and analytic continuation.
Formal Definitions and Notation
The Lambert series is defined as \( L(q) = \sum_{n=1}^\infty \frac{a_n q^n}{1 - q^n} \) where \(|q| < 1\) and \(a_n\) is an arithmetic function. The Dirichlet series is expressed as \( D(s) = \sum_{n=1}^\infty \frac{a_n}{n^s} \) for complex \(s\) with real part greater than some bound to ensure convergence. These series differ in their domain and functional structure, with the Lambert series involving a geometric series denominator and the Dirichlet series using powers of integers weighted by \(n^{-s}\).
Convergence Criteria and Domains
Lambert series converge in domains where the absolute value of the variable is less than one, typically requiring |q| < 1 for series of the form \( \sum_{n=1}^\infty a_n \frac{q^n}{1-q^n} \). Dirichlet series, expressed as \( \sum_{n=1}^\infty \frac{a_n}{n^s} \), converge in half-planes of the complex plane where the real part of s exceeds a certain abscissa of convergence, usually denoted by \(\sigma_c\). The convergence criteria for Dirichlet series depend heavily on the growth rate of the coefficients \(a_n\), while Lambert series convergence is closely tied to the magnitude of q within the unit disk.
Key Properties and Theorems
Lambert series are generating functions of the form \(\sum_{n=1}^{\infty} \frac{a_n q^n}{1 - q^n}\), emphasizing divisor sums, while Dirichlet series take the form \(\sum_{n=1}^{\infty} \frac{a_n}{n^s}\), central to analytic number theory. Key properties of Lambert series include their transformation under modular substitutions and direct connection to arithmetic functions such as the divisor function, whereas Dirichlet series are deeply linked to multiplicative functions and have well-studied analytic continuations and functional equations, exemplified by the Riemann zeta function. Theorems such as the Lambert series factorization theorem and the analytic continuation theorems for Dirichlet series highlight their respective roles in number theory and complex analysis.
Examples of Lambert Series
Lambert series are often used in number theory to represent functions like the sum of divisors, with examples such as \( \sum_{n=1}^\infty \frac{q^n}{1 - q^n} \) illustrating their structure. In contrast, Dirichlet series typically take the form \( \sum_{n=1}^\infty \frac{a_n}{n^s} \) and are employed in analytic number theory and complex analysis, exemplified by the Riemann zeta function \( \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} \). Lambert series connect multiplicative functions with q-series expansions, making them useful in partition theory and modular forms, whereas Dirichlet series primarily analyze arithmetic functions through complex variable techniques.
Examples of Dirichlet Series
Dirichlet series, defined as \(\sum_{n=1}^\infty \frac{a_n}{n^s}\), are fundamental in number theory and analytic functions, with classic examples including the Riemann zeta function \(\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}\) and Dirichlet L-functions \(L(s,\chi) = \sum_{n=1}^\infty \frac{\chi(n)}{n^s}\). These series converge in half-planes of the complex plane and encode prime distribution, modular forms, and arithmetic progressions. Lambert series, on the other hand, take the form \(\sum_{n=1}^\infty a_n \frac{q^n}{1 - q^n}\) and relate more directly to generating functions in partition theory and q-series.
Analytic and Multiplicative Structures
Lambert series are characterized by sums of the form \(\sum_{n=1}^\infty a_n \frac{q^n}{1-q^n}\), linking multiplicative functions to generating functions with analytic features related to modular forms and q-series. Dirichlet series, such as \(\sum_{n=1}^\infty \frac{a_n}{n^s}\), exhibit deeper connections to multiplicative number theory, with analytic continuations and Euler product decompositions reflecting prime factorization structures. The analytic structure of Lambert series often reveals combinatorial interpretations, while Dirichlet series provide a framework for investigating L-functions and prime distribution via complex analysis.
Applications in Number Theory
Lambert series and Dirichlet series both play crucial roles in analytic number theory, with Lambert series often used to study divisor functions and partition identities due to their generating function properties. Dirichlet series, exemplified by the Riemann zeta function, are fundamental in understanding the distribution of prime numbers and the behavior of arithmetic functions through their Euler product representations. Applications of Lambert series include expressing sums over arithmetic functions, while Dirichlet series are key in proving results related to the density and distribution of primes and in the formulation of L-functions.
Comparative Analysis: Lambert vs Dirichlet Series
Lambert series and Dirichlet series both play crucial roles in analytic number theory, with Lambert series expressed as sums of the form \( \sum_{n=1}^\infty a_n \frac{q^n}{1-q^n} \) and Dirichlet series as \( \sum_{n=1}^\infty \frac{a_n}{n^s} \). Lambert series often arise in the study of partition functions and modular forms due to their connection with q-series, while Dirichlet series serve as generating functions for arithmetic functions and are fundamental in understanding L-functions and the distribution of prime numbers. Unlike Dirichlet series, which converge in half-planes of complex variable s, Lambert series convergence depends on the variable q within the unit disk, reflecting distinct analytic properties critical for number-theoretic applications.
Lambert series Infographic
 libterm.com
libterm.com