Enjoy the freedom of access without any cost, empowering you to explore countless resources and opportunities effortlessly. Free options often provide great value while eliminating financial barriers that might restrict your choices. Discover how embracing free solutions can enhance your experience by reading the rest of the article.
Table of Comparison
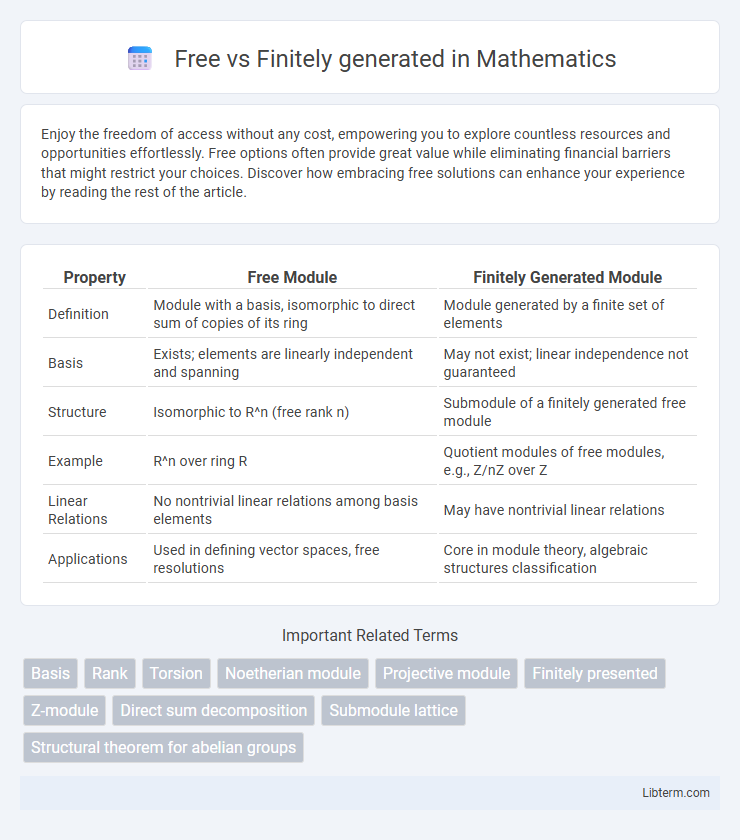
| Property | Free Module | Finitely Generated Module |
|---|---|---|
| Definition | Module with a basis, isomorphic to direct sum of copies of its ring | Module generated by a finite set of elements |
| Basis | Exists; elements are linearly independent and spanning | May not exist; linear independence not guaranteed |
| Structure | Isomorphic to R^n (free rank n) | Submodule of a finitely generated free module |
| Example | R^n over ring R | Quotient modules of free modules, e.g., Z/nZ over Z |
| Linear Relations | No nontrivial linear relations among basis elements | May have nontrivial linear relations |
| Applications | Used in defining vector spaces, free resolutions | Core in module theory, algebraic structures classification |
Introduction to Free and Finitely Generated Structures
Free structures are algebraic systems generated by a set of elements without any relations other than those required by the defining operations, ensuring maximum independence among generators. Finitely generated structures have a finite set of generators from which every element can be derived through the operations of the structure. Understanding the distinction between free and finitely generated entities is crucial in algebra, as free structures provide universal models while finitely generated ones often allow for classification and computational analysis.
Definitions: Free vs Finitely Generated Explained
Free modules are defined as modules that have a basis, meaning every element can be uniquely expressed as a finite linear combination of basis elements with coefficients from the ring. Finitely generated modules require only a finite set of generators, but unlike free modules, these generators may satisfy nontrivial relations, preventing uniqueness of representation. The key difference lies in the presence of a free basis guaranteeing unique decomposition versus finitely generated modules where such uniqueness is not assured.
Key Differences Between Free and Finitely Generated Groups
Free groups consist of elements generated by a set without relations, enabling every element to be uniquely expressed as a reduced word in the generators. Finitely generated groups require only a finite set of generators but may have relations, restricting the structure and allowing multiple representations of elements. The key difference lies in freedom from relations in free groups versus possible constraints and complexity from relations in finitely generated groups.
Examples of Free and Finitely Generated Groups
Free groups, such as the free group on two generators \( F_2 = \langle a, b \rangle \), consist of all reduced words formed from \( a \), \( b \), and their inverses with no relations other than those required by group axioms. Finitely generated groups include free groups generated by a finite set, but also encompass groups like \(\mathbb{Z}^n\), the integer lattice that is finitely generated by \( n \) elements yet not free when \( n > 1 \) due to the presence of relations. The free abelian group \(\mathbb{Z}^n\) serves as a key example illustrating the distinction between free (non-abelian, no relations) and finitely generated groups that may have intrinsic algebraic relations.
Importance in Algebra and Group Theory
Free groups serve as foundational building blocks in algebra and group theory, providing a framework where elements have no relations other than those required by group axioms. Finitely generated groups, characterized by a finite set of generators, are crucial for understanding more complex structures through manageable, finite presentations. The distinction is important as free groups offer universal properties and a basis for constructing other groups, while finitely generated groups enable classification, algorithmic analysis, and practical applications in topology and combinatorial group theory.
Criteria to Determine Freeness or Finite Generation
A module is free if it has a basis, meaning it is isomorphic to a direct sum of copies of its ring, which implies every element can be uniquely expressed as a finite linear combination of basis elements; criteria for freeness involve the existence of such a linearly independent generating set. Finitely generated modules require only a finite set of generators, but these generators need not be linearly independent, hence freeness is a stronger condition than finite generation. Key tests for freeness include checking for bases through linear independence over the ring, while finite generation can be determined by the presence of a finite spanning set without uniqueness.
Applications in Mathematics and Beyond
Free modules provide a flexible framework for constructing objects in algebra, enabling the analysis of vector spaces, group theory, and homological algebra without restriction to bases of finite size. Finitely generated modules appear prominently in computational algebra and algebraic geometry, where they facilitate algorithmic methods for solving polynomial equations and analyzing algebraic varieties. The distinction influences applications in topology, cryptography, and coding theory, where the structure and complexity of modules determine the feasibility and efficiency of mathematical modeling and computations.
Advantages and Limitations of Free Structures
Free structures offer the advantage of providing maximum flexibility by generating elements without imposing relations, making them ideal for constructing bases in algebraic systems such as free groups or modules. Their unrestricted nature ensures straightforward homomorphism extensions, simplifying algebraic computations and theoretical proofs. However, the absence of relations can lead to infinitely large or complex structures, limiting practical applications where finite generation or specific constraints are necessary for manageability and computational feasibility.
The Role of Generators and Relations
In algebra, free modules or groups are characterized by having a basis consisting of generators with no relations beyond those required by the algebraic structure, allowing any element to be uniquely expressed as a linear combination of these generators. Finitely generated modules or groups have a finite set of generators but may impose nontrivial relations among them, limiting the independence of generators and affecting the overall structure. Understanding the interplay between generators and relations is crucial for determining whether a given algebraic object is free or finitely generated, as free objects represent the most unrestricted case while finite generation introduces constraints.
Conclusion: Choosing the Right Structure for Your Needs
Free modules provide maximum flexibility with no relations restricting the basis elements, making them ideal for theoretical exploration and simplifying algebraic computations. Finitely generated modules, while more constrained, offer a practical balance by ensuring a manageable and computable structure important for applications in algebraic geometry and module theory. Selecting between free and finitely generated modules hinges on the need for either unrestricted basis independence or a structured, finite generation suited to computational and applied contexts.
Free Infographic
 libterm.com
libterm.com