A subset is a set containing some or all elements of another set, defined by specific inclusion criteria. Understanding subsets is essential for grasping fundamental concepts in mathematics, logic, and computer science. Explore the rest of the article to deepen your knowledge of subsets and their practical applications.
Table of Comparison
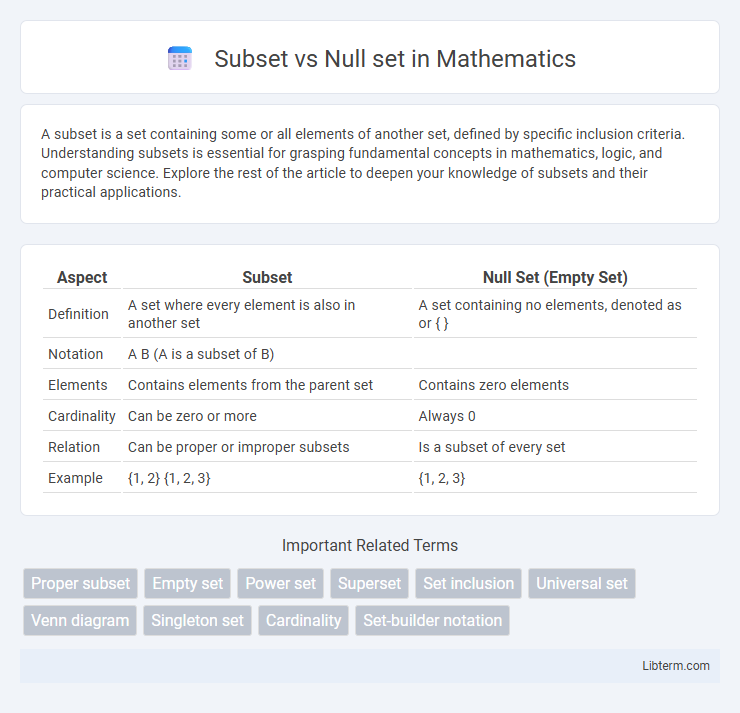
| Aspect | Subset | Null Set (Empty Set) |
|---|---|---|
| Definition | A set where every element is also in another set | A set containing no elements, denoted as or { } |
| Notation | A B (A is a subset of B) | |
| Elements | Contains elements from the parent set | Contains zero elements |
| Cardinality | Can be zero or more | Always 0 |
| Relation | Can be proper or improper subsets | Is a subset of every set |
| Example | {1, 2} {1, 2, 3} | {1, 2, 3} |
Definition of Subset
A subset is a set in which every element of the subset is also an element of another set, denoted as A B, meaning all elements of A are contained within B. The null set, or empty set, is a unique subset that contains no elements and is a subset of every set by definition. Understanding subsets is fundamental in set theory as it establishes hierarchical relationships between sets and is crucial for operations such as union, intersection, and difference.
Definition of Null Set
A null set, also known as an empty set, is defined as a set containing no elements, symbolized by or {}. Every null set is a subset of any set because it satisfies the condition of having no elements outside the given set. The distinction between subsets and null sets lies in the null set being a unique subset with zero elements, while subsets can have any number of elements from the parent set.
Key Differences Between Subset and Null Set
A subset is a set where every element belongs to another set, while a null set, or empty set, contains no elements at all. The null set is a subset of every set, but not every subset is a null set. Subsets can have varying numbers of elements, whereas the null set always has zero elements.
Symbolic Representation
The subset is symbolized by \( A \subseteq B \), indicating every element of set A is also in set B, while the null set is represented by \( \emptyset \) or \(\{\}\), denoting a set with no elements. In symbolic notation, \( \emptyset \subseteq A \) holds true for any set A, since the null set is a subset of all sets by definition. The distinction between these symbols is crucial for understanding set theory operations and relationships.
Examples of Subsets
A subset is a set where every element of set A is also an element of set B, such as {1, 2} being a subset of {1, 2, 3, 4}. The null set, or empty set, denoted by , contains no elements and is considered a subset of every set, including {1, 2, 3}. Examples of subsets include {apple, banana} being a subset of {apple, banana, cherry}, and {2, 4} being a subset of even numbers like {0, 2, 4, 6}.
Examples of Null Set
The null set, also known as the empty set, contains no elements and is denoted by or {}. For example, the set of natural numbers less than zero or the set of solutions to the equation x^2 + 1 = 0 over real numbers are both null sets. Every null set is a subset of any set because it trivially satisfies the subset condition with no elements to contradict membership.
Subset Relations Involving the Null Set
The null set, denoted by , is a subset of every set because it contains no elements that could violate membership conditions. For any set A, the relation A holds universally, establishing the null set as the smallest subset in set theory. This property is fundamental in defining subset relations and ensures consistency in operations like unions, intersections, and power sets.
Practical Applications in Mathematics
In mathematics, subsets are essential for defining and analyzing structures within sets, such as identifying solution sets in algebra or specifying domains in functions. The null set, or empty set, plays a crucial role in establishing base cases in proofs, particularly in induction and set theory, ensuring logical consistency when no elements satisfy a condition. Practical applications include database queries where subsets represent filtered data, while recognizing empty sets helps detect when queries return no results, optimizing computational processes.
Common Misconceptions
A common misconception is that the null set is considered a subset of every set, but it is actually the unique subset containing no elements, which is true by definition in set theory. Another misunderstanding is confusing a subset with a proper subset; a subset can be equal to the original set, while a proper subset must be strictly contained within the set. Clarifying these distinctions helps prevent errors in set notation and logical reasoning within mathematics and computer science.
Summary: Subset vs Null Set
A subset is a set where every element is contained within another set, including the possibility of being equal to that set. The null set, also known as the empty set, contains no elements and is considered a subset of every set. Understanding that the null set is a unique subset with zero elements helps clarify its role in set theory and mathematical logic.
Subset Infographic
 libterm.com
libterm.com