Non-neutral Tannakian categories extend the classical Tannakian formalism by allowing fiber functors that take values in more general fields or rings instead of just algebraically closed fields. These categories play a crucial role in understanding representations of group schemes over non-algebraically closed bases and provide a framework for studying algebraic and arithmetic geometry. Explore the rest of the article to deepen your understanding of how non-neutral Tannakian categories influence modern mathematical research.
Table of Comparison
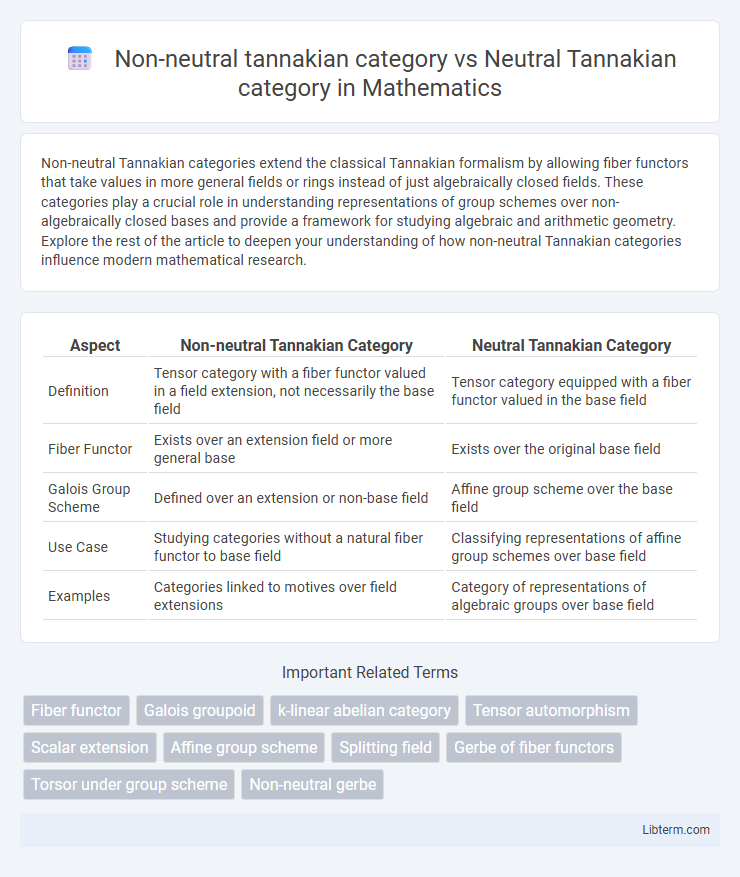
| Aspect | Non-neutral Tannakian Category | Neutral Tannakian Category |
|---|---|---|
| Definition | Tensor category with a fiber functor valued in a field extension, not necessarily the base field | Tensor category equipped with a fiber functor valued in the base field |
| Fiber Functor | Exists over an extension field or more general base | Exists over the original base field |
| Galois Group Scheme | Defined over an extension or non-base field | Affine group scheme over the base field |
| Use Case | Studying categories without a natural fiber functor to base field | Classifying representations of affine group schemes over base field |
| Examples | Categories linked to motives over field extensions | Category of representations of algebraic groups over base field |
Introduction to Tannakian Categories
Tannakian categories, fundamental in modern algebraic geometry and representation theory, classify fiber functors and the associated affine group schemes. Neutral Tannakian categories possess a fiber functor to vector spaces over a fixed field, enabling equivalence with representations of a pro-algebraic group. Non-neutral Tannakian categories lack such a fiber functor, exhibiting more general structures linked to torsors and gerbes instead of group schemes, reflecting a broader scope in categorical duality.
Basic Concepts in Tannakian Theory
Non-neutral Tannakian categories generalize neutral Tannakian categories by lacking a fiber functor to the category of vector spaces over the base field, leading to the need for fiber functors valued in more general tensor categories. Neutral Tannakian categories are rigid, abelian tensor categories equipped with a fiber functor to vector spaces, which allows them to be equivalently described by the category of representations of an affine group scheme. The fundamental distinction lies in the presence of a fiber functor defined over the base field, crucial for reconstructing affine group schemes and understanding Tannakian duality.
Definition of Neutral Tannakian Categories
Neutral Tannakian categories are rigid abelian tensor categories equipped with a fiber functor to the category of finite-dimensional vector spaces over a field, allowing reconstruction of the category as the representation category of an affine group scheme. In contrast, non-neutral Tannakian categories lack such a fiber functor to vector spaces over the base field, requiring fiber functors over field extensions or more general fiber functors. The defining feature of neutral Tannakian categories is the existence of an exact faithful tensor functor to vector spaces over the base field, enabling a Tannakian duality equivalence.
Definition of Non-neutral Tannakian Categories
Non-neutral Tannakian categories are tensor categories equipped with a fiber functor to the category of vector bundles over a base scheme, rather than to vector spaces over a field, distinguishing them from neutral Tannakian categories that admit a fiber functor to finite-dimensional vector spaces over a field. The key feature is that non-neutral Tannakian categories do not necessarily have a fiber functor to the category of vector spaces over a fixed field, reflecting their dependence on a more general base scheme, leading to torsors under affine group schemes rather than affine group schemes themselves. This generalization allows modeling categories of sheaves or representations where no global fiber functor exists, highlighting their importance in the study of fundamental group schemes and algebraic stacks.
Key Differences: Neutral vs Non-neutral Tannakian
Neutral Tannakian categories admit a fiber functor to the category of vector spaces over a field, enabling reconstruction of an affine group scheme via Tannaka duality, while non-neutral Tannakian categories lack such a fiber functor, corresponding instead to torsors under an affine group scheme. In neutral cases, the category is equivalent to the representations of an affine group scheme defined over the base field, whereas non-neutral categories require extension of scalars or base changes to realize a fiber functor. The presence or absence of a neutral fiber functor fundamentally distinguishes the representation-theoretic and geometric interpretations of the two categories in algebraic geometry and category theory.
The Role of Fiber Functors
Fiber functors in neutral Tannakian categories provide a faithful exact tensor functor to the category of vector spaces over a field, enabling a reconstruction of the Tannakian group as a pro-algebraic group over that field. In non-neutral Tannakian categories, fiber functors target vector bundles or more general objects over schemes, reflecting a gerbe structure that obstructs the existence of a global fiber functor to vector spaces alone. This distinction highlights how non-neutral categories require a more intricate framework to capture symmetries via fiber functors, extending beyond the classical neutral setting.
Galois Groups in Tannakian Categories
Neutral Tannakian categories correspond to representations of an affine group scheme over a base field, where the existence of a fiber functor defines a neutral Galois group encapsulating symmetries of the category. Non-neutral Tannakian categories lack a global fiber functor and instead relate to torsors under a Galois group, reflecting forms of the symmetry that are twisted by descent data. The distinction between neutral and non-neutral cases directly impacts the structure and classification of Tannakian Galois groups, influencing fundamental group schemes associated with categories of motives or sheaves.
Examples of Neutral Tannakian Categories
Neutral Tannakian categories are rigid abelian tensor categories equipped with a fiber functor to finite-dimensional vector spaces over a fixed field, typical examples include the category of finite-dimensional representations of an affine group scheme over a field, such as the category of finite-dimensional representations of the fundamental group of a topological space or the category of finite-dimensional representations of an algebraic group. Non-neutral Tannakian categories lack a fiber functor to vector spaces over the base field but admit fiber functors valued in vector spaces over some extension field or more general settings. The category of lisse l-adic sheaves on a scheme over a field that is not algebraically closed serves as a prominent example of a non-neutral Tannakian category, contrasting with the neutral case where the existence of a fiber functor ensures a more straightforward equivalence with representation categories.
Examples of Non-neutral Tannakian Categories
Non-neutral Tannakian categories arise naturally as categories of representations of group schemes over non-algebraically closed fields or more general base schemes, unlike neutral Tannakian categories which correspond to representations over algebraically closed fields with a fiber functor to vector spaces. An example includes the category of l-adic representations of the absolute Galois group of a number field, which forms a non-neutral Tannakian category due to the absence of a fiber functor to finite-dimensional vector spaces over that field. Another example is the category of motives over a general base scheme where no natural fiber functor to vector spaces exists, illustrating the broader complexity and geometric applications of non-neutral Tannakian theory.
Applications and Implications in Modern Mathematics
Non-neutral Tannakian categories extend the framework of neutral Tannakian categories by allowing fiber functors valued in non-algebraically closed fields or more general base categories, enabling the study of phenomena such as motives over non-closed fields and connections with Galois cohomology. Applications in modern mathematics include understanding the symmetry and classification of algebraic structures in arithmetic geometry, particularly in the theory of motives, periods, and fundamental groups of schemes where no neutral fiber functor exists. The implications of this generalization deepen insights into equivalences of categories and group schemes beyond classical settings, influencing research in algebraic geometry, number theory, and quantum groups.
Non-neutral tannakian category Infographic
 libterm.com
libterm.com