The pushforward functor is a key concept in category theory and algebraic geometry, mapping objects and morphisms along a continuous or structure-preserving function between spaces. It translates data from one context to another, preserving relationships and enabling the study of geometric or algebraic properties through image spaces. Explore the rest of the article to deepen your understanding of how the pushforward functor operates and its applications.
Table of Comparison
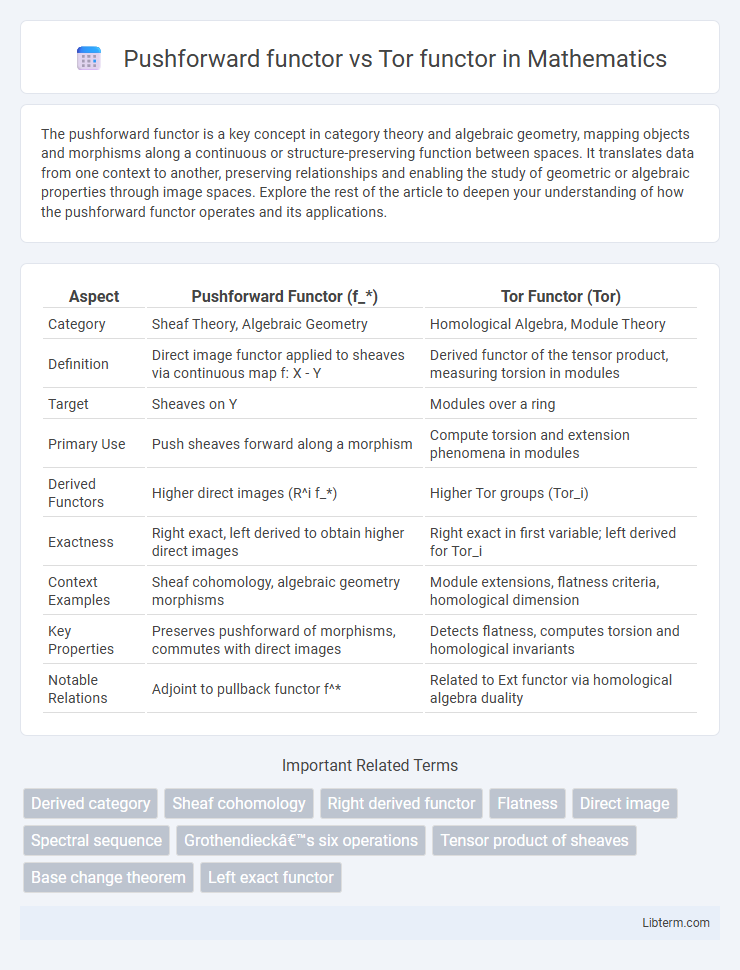
| Aspect | Pushforward Functor (f_*) | Tor Functor (Tor) |
|---|---|---|
| Category | Sheaf Theory, Algebraic Geometry | Homological Algebra, Module Theory |
| Definition | Direct image functor applied to sheaves via continuous map f: X - Y | Derived functor of the tensor product, measuring torsion in modules |
| Target | Sheaves on Y | Modules over a ring |
| Primary Use | Push sheaves forward along a morphism | Compute torsion and extension phenomena in modules |
| Derived Functors | Higher direct images (R^i f_*) | Higher Tor groups (Tor_i) |
| Exactness | Right exact, left derived to obtain higher direct images | Right exact in first variable; left derived for Tor_i |
| Context Examples | Sheaf cohomology, algebraic geometry morphisms | Module extensions, flatness criteria, homological dimension |
| Key Properties | Preserves pushforward of morphisms, commutes with direct images | Detects flatness, computes torsion and homological invariants |
| Notable Relations | Adjoint to pullback functor f^* | Related to Ext functor via homological algebra duality |
Introduction to Pushforward and Tor Functors
The pushforward functor, often denoted as \( f_* \), is a fundamental construct in sheaf theory and algebraic geometry that maps sheaves from a space X to its image under a morphism \( f: X \to Y \). The Tor functor, \( \mathrm{Tor}_n^R(-,-) \), arises in homological algebra as a derived functor of the tensor product, measuring the extent to which tensoring fails to be exact and capturing torsion phenomena in module categories over a ring R. Understanding the pushforward functor involves its exactness properties and role in direct image sheaves, while the Tor functor is crucial for analyzing extensions and relations between modules via projective resolutions.
Defining the Pushforward Functor
The pushforward functor, denoted as \( f_* \), arises in category theory and algebraic geometry to map sheaves or modules from one space to another via a continuous or morphism \( f \). It is defined by taking a sheaf \( \mathcal{F} \) on space \( X \) and associating to each open set \( U \subseteq Y \) the sections of \( \mathcal{F} \) over \( f^{-1}(U) \), specifically \( (f_*\mathcal{F})(U) = \mathcal{F}(f^{-1}(U)) \). This construction contrasts with the Tor functor, which measures the failure of flatness by deriving the tensor product, while the pushforward functor preserves direct images and is often left exact but not necessarily exact.
Understanding the Tor Functor
The Tor functor, derived from the tensor product, measures the extent to which tensoring fails to be exact and captures information about the extensions and relations between modules over a ring. Unlike the pushforward functor, which deals with the direct image of sheaves under a continuous map in topology or algebraic geometry, the Tor functor operates in homological algebra to quantify torsion phenomena in modules. Calculating Tor groups reveals hidden syzygies and detects how modules behave under base change, making it a crucial tool for understanding extensions and flatness properties in module theory.
Categorical Framework of Pushforward Functor
The pushforward functor \( f_* \) in the categorical framework acts as a right adjoint to the pullback functor \( f^* \), facilitating the transfer of sheaves along continuous maps in a contravariant manner. Tor functors \( \mathrm{Tor}_i^R(-,-) \), derived from tensor product, measure the failure of exactness in tensoring modules over a ring \( R \), capturing homological information of module extensions. Within derived categories, the pushforward functor corresponds to \( Rf_* \), a right derived functor preserving limits, whereas Tor functors arise as left derived functors related to homological algebra and do not directly coincide with pushforwards but instead reflect the deeper structure of module interactions.
Homological Algebra and Tor Functor
The pushforward functor, often denoted by f_*, maps sheaves or modules along a continuous or morphism of schemes, preserving the underlying algebraic structures, while the Tor functor, Tor_i^R(-, -), measures the failure of flatness and computes derived tensor products in homological algebra. Unlike the pushforward functor, Tor functors capture torsion phenomena and provide information on extensions and relations between modules over a ring R by detecting non-projectivity via homology groups. In computations over a ring R, Tor functors appear as left derived functors of the tensor product, playing a fundamental role in detecting flatness, homological dimension, and in spectral sequences related to homology theories.
Relationship Between Pushforward and Tor Functors
The relationship between the pushforward functor and Tor functors emerges in derived category contexts, where the pushforward functor \(f_*\) interacts with derived functors of tensor products, notably Tor. Specifically, for a morphism of ringed spaces \(f: X \to Y\), the derived pushforward \(Rf_*\) relates to Tor via the projection formula, expressing how \(Rf_*(\mathcal{F} \otimes^{\mathbb{L}} f^* \mathcal{G})\) is isomorphic to \(Rf_*\mathcal{F} \otimes^{\mathbb{L}} \mathcal{G}\), reflecting the Tor functor's role in resolving tensor product complexities under pushforward operations. This interplay is fundamental in sheaf cohomology and algebraic geometry, linking pushforward operations with the homological algebra encoded in Tor groups.
Applications in Algebraic Geometry
The pushforward functor, denoted \( f_* \), is extensively used in algebraic geometry to transfer sheaves along morphisms of schemes, enabling the study of global sections and cohomology on target spaces. The Tor functor measures the derived tensor product's homological behavior, providing crucial insights into flatness criteria and the interactions between sheaves in exact sequences. In applications such as deformation theory and intersection theory, the pushforward functor facilitates the global analysis of sheaf cohomology, while the Tor functor helps compute obstructions and control local-to-global spectral sequences.
Applications in Commutative Algebra
The pushforward functor (direct image functor) in commutative algebra is crucial for relating modules over different rings via ring homomorphisms, particularly in studying module behavior under base change and in algebraic geometry contexts. The Tor functor measures the failure of flatness and detects extension obstructions by computing derived tensor products, which is essential for resolving module structures and understanding depth and regularity properties of rings. Applications of the pushforward functor include analyzing morphisms of schemes and coherent sheaves, while the Tor functor is widely employed in resolving projective dimension and calculating local cohomology in commutative algebra.
Comparative Examples and Key Differences
The pushforward functor, denoted \(f_*\), transfers sheaves along a continuous map \(f: X \to Y\) and preserves direct images, typically used in sheaf theory and algebraic geometry for analyzing morphisms between spaces. In contrast, the Tor functor, \(\mathrm{Tor}_i^R(-,-)\), arises in homological algebra as a derived functor of the tensor product, measuring the failure of flatness and capturing extension-related torsion phenomena over a ring \(R\). While \(f_*\) relates geometric objects via continuous mappings and preserves exactness on the left, \(\mathrm{Tor}\) provides homological invariants detecting non-projectivity of modules, exemplified by \(f_*\mathcal{O}_X\) pushing forward structure sheaves compared with \(\mathrm{Tor}_i^R(M,N)\) revealing hidden torsion layers in ring modules.
Summary and Further Reading
The pushforward functor, often denoted as \( f_* \), transfers sheaves along a continuous map \( f: X \to Y \), preserving the sheaf structure but not necessarily exactness, playing a crucial role in derived functor cohomology. The Tor functor, \(\mathrm{Tor}_i^R(-, -)\), measures the failure of flatness in modules over a ring \(R\) and quantifies extensions and relations in homological algebra, essential in computing tensor product derived functors. For further reading, foundational texts include Weibel's *An Introduction to Homological Algebra* for Tor functors and Hartshorne's *Algebraic Geometry* for sheaf pushforwards and their derived categories.
Pushforward functor Infographic
 libterm.com
libterm.com