An essential submodule is a critical component within a larger system, designed to perform specific, indispensable functions that ensure overall stability and functionality. It integrates seamlessly with other modules, providing foundational support and enhancing the system's efficiency. Explore the rest of the article to understand how essential submodules can optimize your system's performance.
Table of Comparison
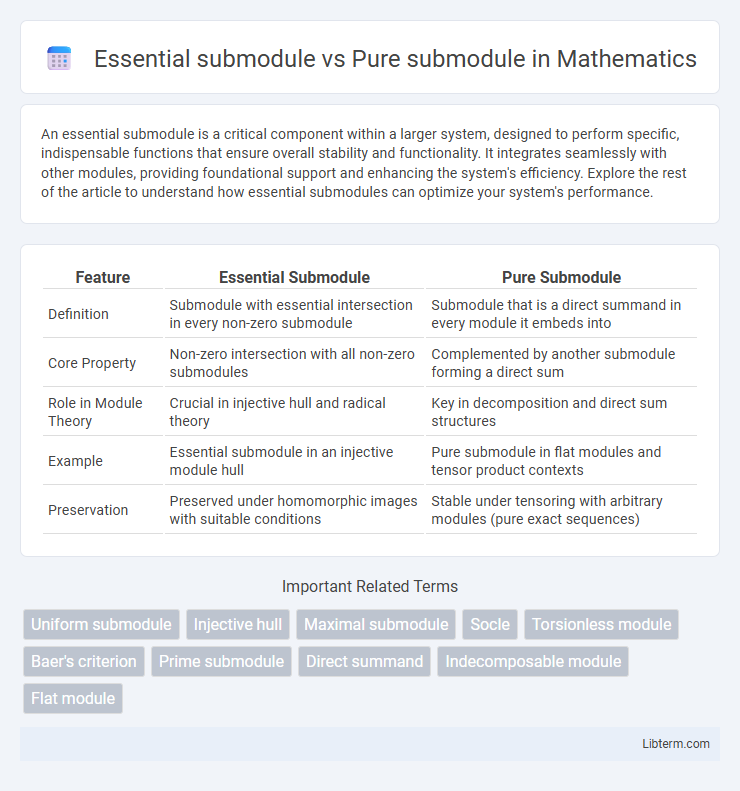
| Feature | Essential Submodule | Pure Submodule |
|---|---|---|
| Definition | Submodule with essential intersection in every non-zero submodule | Submodule that is a direct summand in every module it embeds into |
| Core Property | Non-zero intersection with all non-zero submodules | Complemented by another submodule forming a direct sum |
| Role in Module Theory | Crucial in injective hull and radical theory | Key in decomposition and direct sum structures |
| Example | Essential submodule in an injective module hull | Pure submodule in flat modules and tensor product contexts |
| Preservation | Preserved under homomorphic images with suitable conditions | Stable under tensoring with arbitrary modules (pure exact sequences) |
Understanding Submodules in Module Theory
Essential submodules in module theory are submodules that intersect non-trivially with every non-zero submodule of the parent module, ensuring their indispensability in structural analysis. Pure submodules, by contrast, preserve the solvability of linear equations over the base ring, maintaining exact sequences upon tensoring and reflecting intrinsic module properties. Understanding the distinction aids in clarifying how submodules influence module decompositions and homological characterizations within algebraic systems.
Defining Essential Submodules
Essential submodules of a module M over a ring R are submodules N such that every nonzero submodule of M has a nonzero intersection with N, making N indispensable to the module's structure. Pure submodules, on the other hand, are characterized by the property that the tensor product with any R-module preserves exact sequences, reflecting a type of algebraic purity. Defining an essential submodule involves verifying that for every nonzero element in M, there exists a nonzero overlap with N, which is crucial in understanding injective hulls and module decomposition.
What is a Pure Submodule?
A Pure Submodule is a type of submodule in software development characterized by containing code that is independent and self-contained, making it easily reusable across different projects without requiring external dependencies. Unlike Essential Submodules, which include core functionalities critical to the main module's operation, Pure Submodules focus on modularity and maintainability by isolating specific features or utilities. This separation enhances flexibility in code management, allowing developers to update or replace Pure Submodules without impacting the overall system stability.
Key Differences between Essential and Pure Submodules
Essential submodules contain elements that are crucial for the structure and function of a module, often intersecting non-trivially with every non-zero submodule, while pure submodules maintain exact sequences under tensor products, preserving module properties more flexibly. Essential submodules are characterized by their indispensability in encompassing non-zero submodules, whereas pure submodules focus on preserving the integrity of module homomorphisms, particularly in relation to flat modules. The key difference lies in their interaction with module operations: essential submodules enforce containment and influence, whereas pure submodules ensure structural stability under functorial operations like tensoring.
Properties of Essential Submodules
Essential submodules possess the key property that their intersection with any nonzero submodule is nontrivial, ensuring they are dense within the parent module. This property guarantees that any homomorphism vanishing on an essential submodule must be zero, highlighting their significance in module theory. Pure submodules differ as they preserve exact sequences under tensor products, but essential submodules are primarily characterized by their embedding strength and intersection behavior within modules.
Properties of Pure Submodules
Pure submodules preserve exact sequences under tensoring, ensuring that for any module M, the sequence 0 - P M - N M remains exact when P is a pure submodule of N. This property distinguishes pure submodules from essential submodules, which require every nonzero submodule of N to intersect P nontrivially but do not guarantee preservation under tensor products. Pure submodules also correspond to flatness conditions and are characterized by solutions to linear systems lifting from N to P, making them crucial in homological algebra and module theory.
Examples of Essential versus Pure Submodules
Essential submodules include any non-zero submodule that intersects non-trivially with every other non-zero submodule, such as the socle of a module in representation theory. Pure submodules, by contrast, maintain the property that the exactness of sequences is preserved when tensored with any module; for example, any direct summand of a free module is pure, but not necessarily essential. In practice, the submodule of all torsion elements in an abelian group is essential, while the inclusion of an ideal in a ring that splits as a direct summand exemplifies a pure submodule.
Applications of Essential and Pure Submodules
Essential submodules find critical applications in module theory and homological algebra, serving to understand extensions and injective hulls by ensuring that any nonzero submodule intersects the essential submodule nontrivially. Pure submodules are fundamental in model theory and algebraic geometry, where purity enables preservation of exact sequences under tensor products and facilitates analysis of flatness and localization properties. Both concepts play pivotal roles in structure theory of modules, with essential submodules highlighting irreducibility and purity supporting decomposition and base change operations.
Common Misconceptions about Submodules
Essential submodules are often confused with pure submodules, but essential submodules require every nonzero submodule to intersect nontrivially, while pure submodules preserve exact sequences after tensoring with any module. A common misconception is that purity implies essentiality, whereas they represent fundamentally different properties in module theory. Understanding this distinction is crucial for correctly analyzing submodule behaviors in algebraic structures.
Choosing between Essential and Pure Submodules in Algebra
Choosing between essential and pure submodules in algebra depends on the structural properties desired within a module. Essential submodules intersect non-trivially with every non-zero submodule, ensuring a robust embedding, while pure submodules maintain exactness under tensor products, preserving algebraic relations at a more refined level. For applications requiring stability under extension and homological purity, pure submodules are ideal; essential submodules are preferred when capturing core structural components within complex module hierarchies.
Essential submodule Infographic
 libterm.com
libterm.com