An identity matrix is a square matrix with ones on the main diagonal and zeros elsewhere, playing a crucial role in linear algebra as the multiplicative identity for matrices. It leaves any matrix unchanged when multiplied, making it essential for solving systems of equations and matrix operations. Explore the rest of the article to understand how identity matrices function and their applications in various mathematical contexts.
Table of Comparison
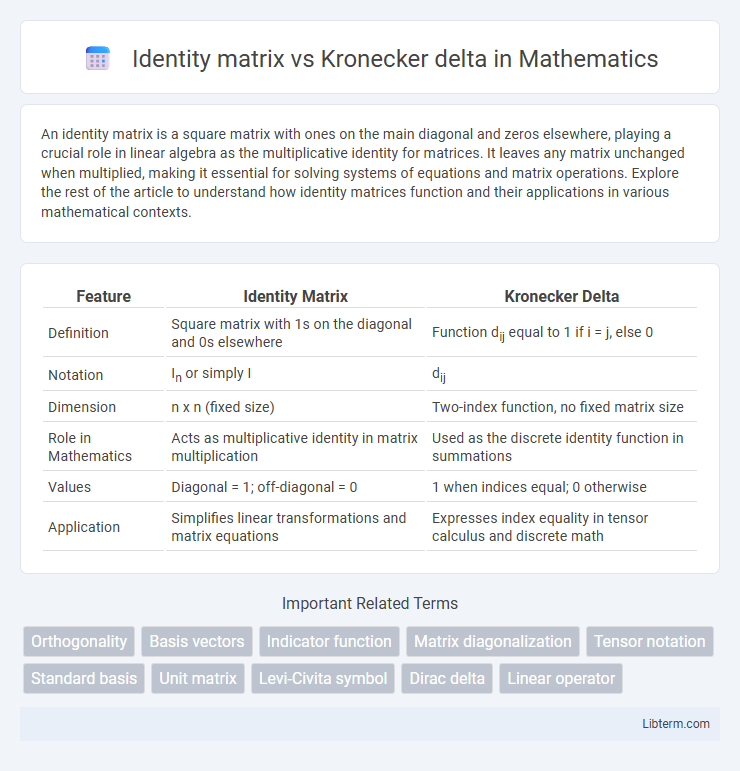
| Feature | Identity Matrix | Kronecker Delta |
|---|---|---|
| Definition | Square matrix with 1s on the diagonal and 0s elsewhere | Function dij equal to 1 if i = j, else 0 |
| Notation | In or simply I | dij |
| Dimension | n x n (fixed size) | Two-index function, no fixed matrix size |
| Role in Mathematics | Acts as multiplicative identity in matrix multiplication | Used as the discrete identity function in summations |
| Values | Diagonal = 1; off-diagonal = 0 | 1 when indices equal; 0 otherwise |
| Application | Simplifies linear transformations and matrix equations | Expresses index equality in tensor calculus and discrete math |
Introduction to Identity Matrix and Kronecker Delta
The identity matrix is a square matrix with ones on the main diagonal and zeros elsewhere, serving as the multiplicative identity in matrix algebra. The Kronecker delta, defined as d_ij = 1 if i = j and 0 otherwise, acts as the discrete analog of the identity matrix in index notation. Both are fundamental in linear algebra, with the identity matrix used in matrix multiplication and the Kronecker delta used in summation over indices.
Defining the Identity Matrix
The identity matrix is a square matrix with ones on the main diagonal and zeros elsewhere, serving as the multiplicative identity in matrix algebra. Each element \(I_{ij}\) is defined by the Kronecker delta \(\delta_{ij}\), where \(\delta_{ij} = 1\) if \(i = j\) and \(0\) otherwise. This direct relationship highlights how the Kronecker delta provides the formal definition for the identity matrix entries in linear algebra.
Understanding the Kronecker Delta
The Kronecker delta, denoted as d_ij, is a function that equals 1 when the indices i and j are equal and 0 otherwise, serving as an essential tool in summation notation and discrete mathematics. Unlike the identity matrix, which is a square matrix with ones on the diagonal and zeros elsewhere, the Kronecker delta functions as a scalar value used to simplify expressions involving indexed variables. Understanding the Kronecker delta helps clarify its role in linear algebra, tensor analysis, and physics by acting as an identity element in summations and index manipulations.
Mathematical Notation and Representation
The identity matrix, denoted as \( I_n \), is an \( n \times n \) square matrix with ones on the main diagonal and zeros elsewhere, mathematically expressed as \( (I_n)_{ij} = \delta_{ij} \). The Kronecker delta \( \delta_{ij} \) is a two-index function defined as \( \delta_{ij} = 1 \) if \( i = j \) and \( 0 \) otherwise, serving as the fundamental scalar element representing the identity matrix components. In tensor notation, the identity matrix elements correspond directly to the Kronecker delta, establishing a one-to-one relationship between matrix representation and scalar indicator functions.
Key Properties and Characteristics
The identity matrix is a square matrix with ones on the main diagonal and zeros elsewhere, serving as the multiplicative identity in matrix algebra. The Kronecker delta, d_ij, is a function equal to 1 when indices i and j are equal, and 0 otherwise, often representing elements of the identity matrix in index notation. Both share the key property of preserving vector components during transformations, with the identity matrix acting on vectors and matrices, while the Kronecker delta operates as a discrete selector in summations and tensor formulations.
Differences in Mathematical Operations
The identity matrix is a square matrix with ones on the diagonal and zeros elsewhere, serving as the multiplicative identity in matrix multiplication, preserving vector or matrix dimensions. The Kronecker delta, d_ij, is a function of two variables that equals 1 when the indices are equal and 0 otherwise, commonly used to simplify summations and represent discrete identity relations in tensor calculus. Unlike matrix multiplication with the identity matrix, operations involving the Kronecker delta often occur in index notation and do not involve matrix dimensionality or multiplication but rather serve as a symbolic selector or filtering tool.
Applications in Linear Algebra
The identity matrix serves as the multiplicative identity in linear algebra, maintaining vector or matrix dimensions while preserving data during transformations. The Kronecker delta functions as a discrete indicator, simplifying summation expressions and helping define orthogonality in vector spaces. Both tools are essential in matrix computations, eigenvalue problems, and tensor representations, providing foundational support for solving linear systems and performing coordinate transformations.
Role in Tensors and Matrix Calculations
The identity matrix serves as the multiplicative identity in matrix operations, maintaining vector or tensor values without alteration, essential for preserving magnitude and direction in transformations. The Kronecker delta functions as a discrete symbol representing the identity element in tensor notation, enabling index substitution and simplification in summation processes involving tensors. Both play crucial roles in tensor calculations: the identity matrix operates in explicit matrix form, while the Kronecker delta provides an index-level tool facilitating tensor contraction and manipulation.
Common Misconceptions
The identity matrix and the Kronecker delta are often confused due to their similar notation and role in linear algebra, but they represent distinct concepts: the identity matrix is a square matrix with ones on the diagonal and zeros elsewhere, while the Kronecker delta is a function d_ij equal to 1 if i = j and 0 otherwise. A common misconception is treating the Kronecker delta as a matrix rather than an index-based function used to simplify summations in tensor operations. Understanding that the identity matrix operates on vectors and matrices, whereas the Kronecker delta acts as an indexing tool in summations, resolves most misunderstandings between these two fundamental objects.
Conclusion: Comparing Identity Matrix and Kronecker Delta
The identity matrix and Kronecker delta both serve as fundamental components in linear algebra and tensor analysis, with the identity matrix being a square matrix with ones on the diagonal and zeros elsewhere, representing the identity transformation. The Kronecker delta functions as a discrete symbol d_ij that equals 1 when indices i and j are equal and 0 otherwise, effectively acting as the components of the identity matrix in index notation. In conclusion, while the identity matrix is a concrete matrix representation used in computations, the Kronecker delta provides an abstract, index-based representation that simplifies notation and proofs in mathematical and physical contexts.
Identity matrix Infographic
 libterm.com
libterm.com