Periodic patterns play a crucial role in various scientific fields, from physics to biology, revealing consistent behaviors and cycles in natural phenomena. Understanding these repetitive sequences can help you predict and analyze trends effectively. Explore the rest of the article to discover how periodicity influences different aspects of life and technology.
Table of Comparison
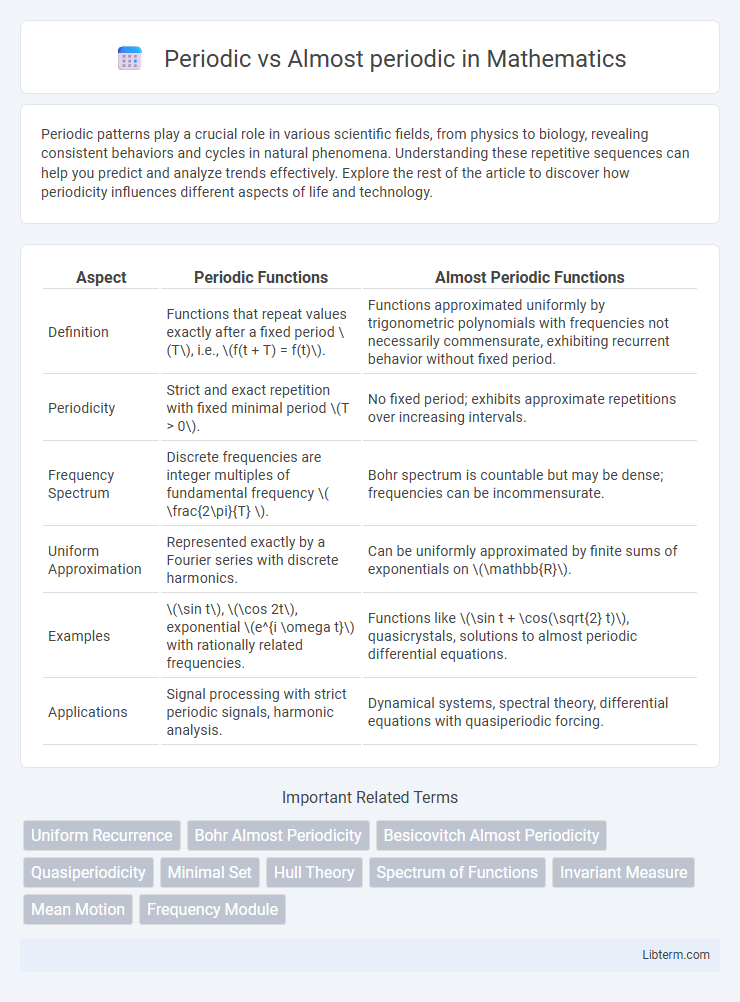
| Aspect | Periodic Functions | Almost Periodic Functions |
|---|---|---|
| Definition | Functions that repeat values exactly after a fixed period \(T\), i.e., \(f(t + T) = f(t)\). | Functions approximated uniformly by trigonometric polynomials with frequencies not necessarily commensurate, exhibiting recurrent behavior without fixed period. |
| Periodicity | Strict and exact repetition with fixed minimal period \(T > 0\). | No fixed period; exhibits approximate repetitions over increasing intervals. |
| Frequency Spectrum | Discrete frequencies are integer multiples of fundamental frequency \( \frac{2\pi}{T} \). | Bohr spectrum is countable but may be dense; frequencies can be incommensurate. |
| Uniform Approximation | Represented exactly by a Fourier series with discrete harmonics. | Can be uniformly approximated by finite sums of exponentials on \(\mathbb{R}\). |
| Examples | \(\sin t\), \(\cos 2t\), exponential \(e^{i \omega t}\) with rationally related frequencies. | Functions like \(\sin t + \cos(\sqrt{2} t)\), quasicrystals, solutions to almost periodic differential equations. |
| Applications | Signal processing with strict periodic signals, harmonic analysis. | Dynamical systems, spectral theory, differential equations with quasiperiodic forcing. |
Introduction to Periodic and Almost Periodic Functions
Periodic functions repeat their values at fixed, regular intervals defined by a period \(T\), such that \(f(x + T) = f(x)\) for all \(x\). Almost periodic functions generalize this concept by allowing approximate repetitions without a fixed period, maintaining uniform closeness to \(f(x)\) over relatively dense sets of shifts. These functions play a crucial role in harmonic analysis and differential equations, modeling phenomena with quasi-regular oscillations beyond strict periodicity.
Defining Periodicity in Mathematics
Periodic functions in mathematics repeat their values at fixed intervals, defined by a positive period T such that f(t + T) = f(t) for all t in the domain. Almost periodic functions generalize this concept by allowing functions to exhibit recurring patterns that approximate periodicity without a fixed period, maintaining uniform closeness to their shifted versions for relatively dense sets of shifts. The distinction lies in strict repetition for periodic functions versus near-repetition with variable shifts in almost periodic functions, critical in harmonic analysis and differential equations.
What are Almost Periodic Functions?
Almost periodic functions generalize periodic functions by allowing values to recur with arbitrary precision rather than fixed intervals. Unlike strictly periodic functions with a constant period, almost periodic functions exhibit patterns that repeat approximately over time, enabling modeling of more complex natural and engineering phenomena. Bohr and Besicovitch provided foundational frameworks for analyzing these functions through uniform convergence of trigonometric polynomials and mean value properties.
Key Differences: Periodic vs Almost Periodic
Periodic functions repeat their values exactly at regular intervals defined by a fixed period, such as f(t) = f(t + T) for all t and a constant T. Almost periodic functions generalize this concept by allowing approximate repetitions over intervals that are not strictly fixed, maintaining closeness to previous values within any desired accuracy. Key differences include the strict fixed period in periodic functions versus the flexible, quasi-repetitive nature of almost periodic functions, enabling their application in more complex and less uniform systems.
Historical Background and Development
Periodic functions, systematically studied since the 18th century with the foundational work of Joseph Fourier, exhibit strict repetition at fixed intervals, forming the basis of classical harmonic analysis. The concept of almost periodic functions emerged in the early 20th century, introduced by Harald Bohr as a generalization to capture functions exhibiting recurrent behavior without strict periodicity, significantly advancing the field of functional analysis. The development of almost periodicity influenced modern mathematical analysis by enabling the study of more complex dynamical systems and differential equations beyond traditional periodic frameworks.
Mathematical Properties and Formulations
Periodic functions satisfy f(t + T) = f(t) for a fixed period T across all t in their domain, exhibiting exact repetition and enabling Fourier series decomposition into discrete harmonics. Almost periodic functions generalize this concept by allowing functions f(t) to approximate their values arbitrarily closely over relatively dense sets of "almost periods," characterized through Bohr or Bochner formulations that involve uniform convergence and compactness arguments. The spectral analysis for almost periodic functions extends to Bohr spectra, capturing frequencies as limit points, whereas classical periodic functions have purely discrete frequency spectra tied to integer multiples of the fundamental period.
Common Examples in Real-World Applications
Periodic functions, characterized by repeating values at fixed intervals, are common in real-world applications such as clock timekeeping, seasonal temperature variations, and AC electrical currents. Almost periodic functions extend this concept by allowing variable intervals with recurring patterns, seen in signal processing for audio and speech analysis and in biological rhythms like heartbeats and circadian cycles. Both types play crucial roles in fields such as engineering, physics, and biology for modeling repetitive yet sometimes irregular phenomena.
Importance in Fourier Analysis
Periodic functions exhibit exact repetition over fixed intervals, enabling representation by discrete Fourier series with coefficients at integer multiples of a fundamental frequency. Almost periodic functions generalize this concept, allowing for frequencies that are not integer multiples but still produce uniform approximations by finite Fourier sums, thus extending Fourier analysis to more complex signal structures. This distinction is crucial in applications such as signal processing and harmonic analysis, where capturing quasi-repetitive patterns requires the flexibility of almost periodic frameworks beyond strict periodicity.
Challenges and Limitations
Periodic functions exhibit regular, repeating patterns with fixed intervals, making their analysis and prediction straightforward in mathematical and engineering applications. Almost periodic functions generalize periodicity by allowing non-constant, quasi-repeating patterns, but this complexity introduces challenges in accurately characterizing convergence and stability. Limitations include the difficulty in establishing uniform approximations and the increased computational effort required for spectral analysis in almost periodic systems.
Conclusion: Choosing Between Periodic and Almost Periodic Functions
Choosing between periodic and almost periodic functions depends on the system's complexity and signal characteristics; periodic functions suit strictly repetitive signals with fixed intervals, while almost periodic functions accommodate signals with recurring patterns that lack exact repetition but exhibit near-regular behavior. In applications requiring precise frequency analysis, periodic functions offer clarity and computational simplicity, whereas almost periodic functions provide flexibility in modeling signals with multiple incommensurate frequencies. Understanding the trade-offs in predictability and mathematical handling guides optimal function selection for signal processing, control systems, and harmonic analysis.
Periodic Infographic
 libterm.com
libterm.com