A stationary measure is a probability distribution that remains unchanged under the dynamics of a given stochastic process or Markov chain, representing long-term equilibrium behavior. Understanding stationary measures is crucial for analyzing stability, convergence, and invariant properties of random systems. Explore the article to learn how stationary measures impact your analysis of stochastic models and their applications.
Table of Comparison
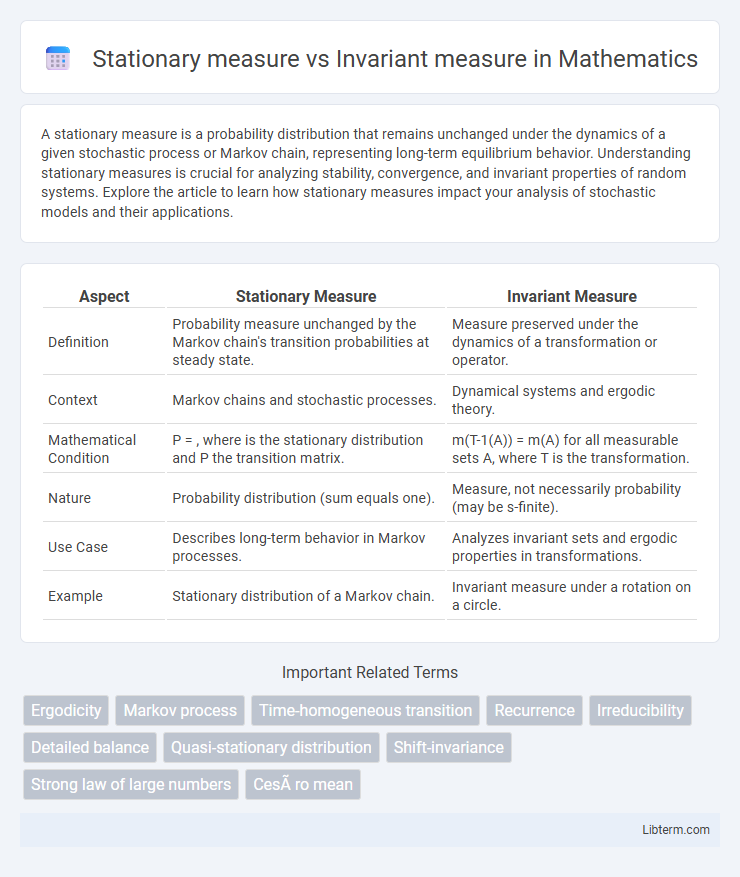
| Aspect | Stationary Measure | Invariant Measure |
|---|---|---|
| Definition | Probability measure unchanged by the Markov chain's transition probabilities at steady state. | Measure preserved under the dynamics of a transformation or operator. |
| Context | Markov chains and stochastic processes. | Dynamical systems and ergodic theory. |
| Mathematical Condition | P = , where is the stationary distribution and P the transition matrix. | m(T-1(A)) = m(A) for all measurable sets A, where T is the transformation. |
| Nature | Probability distribution (sum equals one). | Measure, not necessarily probability (may be s-finite). |
| Use Case | Describes long-term behavior in Markov processes. | Analyzes invariant sets and ergodic properties in transformations. |
| Example | Stationary distribution of a Markov chain. | Invariant measure under a rotation on a circle. |
Introduction to Stationary and Invariant Measures
Stationary measures describe probability distributions that remain unchanged under the dynamics of a Markov process, capturing long-term equilibrium behaviors. Invariant measures generalize this concept to broader dynamical systems, ensuring the measure is preserved under the system's evolution. Both concepts play crucial roles in ergodic theory and stochastic processes, providing foundational tools for analyzing stability and convergence.
Defining Stationary Measures
Stationary measures are probability measures preserved by the transition operator of a Markov process, meaning the distribution remains unchanged over time under the dynamics of the process. Invariant measures are a broader class where the measure remains fixed under a given transformation or flow, often characterizing long-term equilibrium states in dynamical systems. Defining stationary measures involves identifying distributions \(\mu\) satisfying \(\mu P = \mu\), where \(P\) is the transition kernel, ensuring that \(\mu\) is unchanged after one step of the stochastic process.
Understanding Invariant Measures
Invariant measures are probability measures that remain unchanged under the dynamics of a given system or transformation, satisfying the condition m(T-1A) = m(A) for all measurable sets A. These measures provide crucial insight into the long-term behavior of dynamical systems, as they capture stable distributions that persist over time. Invariant measures serve as foundational tools in ergodic theory, enabling the analysis of statistical properties and ensuring consistency in the probabilistic description of system evolution.
Key Differences Between Stationary and Invariant Measures
Stationary measures describe probability distributions that remain constant over time under the evolution of a Markov process, whereas invariant measures are specific stationary measures that also satisfy the detailed balance condition, ensuring time-reversibility. Stationary measures apply broadly to any Markov chain or process preserving distribution, while invariant measures often arise in ergodic theory and reversible stochastic systems. The key difference lies in the stronger symmetry constraints for invariant measures, making them a subset of stationary measures with additional structural properties.
Mathematical Formulation and Examples
A stationary measure \( \mu \) for a Markov chain with transition kernel \( P \) satisfies \( \mu = \mu P \), meaning \( \mu(A) = \int P(x, A) \, d\mu(x) \) for all measurable sets \( A \), ensuring the distribution remains unchanged after one step. An invariant measure generalizes this by requiring \( \mu(T^{-1}(A)) = \mu(A) \) for a measurable transformation \( T \), preserving measure under \( T \). For example, the uniform distribution on the circle is invariant under rotation, while the stationary distribution of a finite Markov chain is a probability vector satisfying \( \pi = \pi P \).
Role in Markov Chains and Stochastic Processes
Stationary measures serve as probability distributions that remain unchanged over time under the dynamics of a Markov chain, reflecting the long-term behavior of the system. Invariant measures generalize this concept by preserving measure under the transition kernel, applicable even beyond probability constraints in stochastic processes. Both are fundamental in analyzing equilibrium properties and ergodicity within Markov chains and broader stochastic models.
Applications in Probability and Statistics
Stationary measures describe distributions that remain unchanged under a given Markov transition kernel, crucial for understanding long-term behavior in stochastic processes and ergodic theory. Invariant measures are fundamental in the analysis of dynamical systems, ensuring that statistical properties persist over time, which aids in modeling equilibrium states in Markov chains and Bayesian statistics. Applications include stability analysis in Markov Chain Monte Carlo methods, where stationary measures guarantee convergence to target distributions and invariant measures support robust inference in time series and random processes.
Conditions for Existence and Uniqueness
Stationary measures exist when a Markov chain or stochastic process exhibits time-homogeneity and the transition probabilities are consistent over iterations, often requiring the chain to be irreducible and positive recurrent for uniqueness. Invariant measures, typically defined for dynamical systems, demand the system's transformation preserve measure, with existence guaranteed under conditions such as compactness and continuity of the transformation. Uniqueness of both measures frequently hinges on ergodicity, where the system or process cannot be decomposed into smaller invariant subsets, ensuring a single, stable distribution.
Practical Implications and Interpretations
Stationary measures represent probability distributions that remain unchanged under the transition dynamics of a Markov process, providing a foundation for long-term behavior analysis in stochastic systems. Invariant measures extend this concept by requiring stability under group actions or transformations, offering broader applicability in ergodic theory and dynamical systems. Practically, stationary measures facilitate prediction of equilibrium states in stochastic modeling, while invariant measures enable characterization of conserved quantities and symmetry properties in complex systems.
Summary and Future Directions
Stationary measures provide a probabilistic description of a process's long-term distribution under repeated application of a transition operator, while invariant measures remain unchanged by the dynamics of the underlying system, often serving as fixed points in measure-preserving transformations. Understanding the conditions under which stationary measures converge to invariant measures offers insight into ergodic properties and stability of stochastic processes. Future research directions include exploring non-Markovian extensions, quantifying convergence rates, and applying these concepts to complex adaptive systems and high-dimensional dynamical models.
Stationary measure Infographic
 libterm.com
libterm.com