Singular refers to the form of a word used to denote one person, place, or thing, distinguishing it from plural forms that indicate more than one. Proper understanding of singular nouns and verbs ensures clear and precise communication in both writing and speech. Explore the rest of this article to master the use of singular forms and improve your language skills.
Table of Comparison
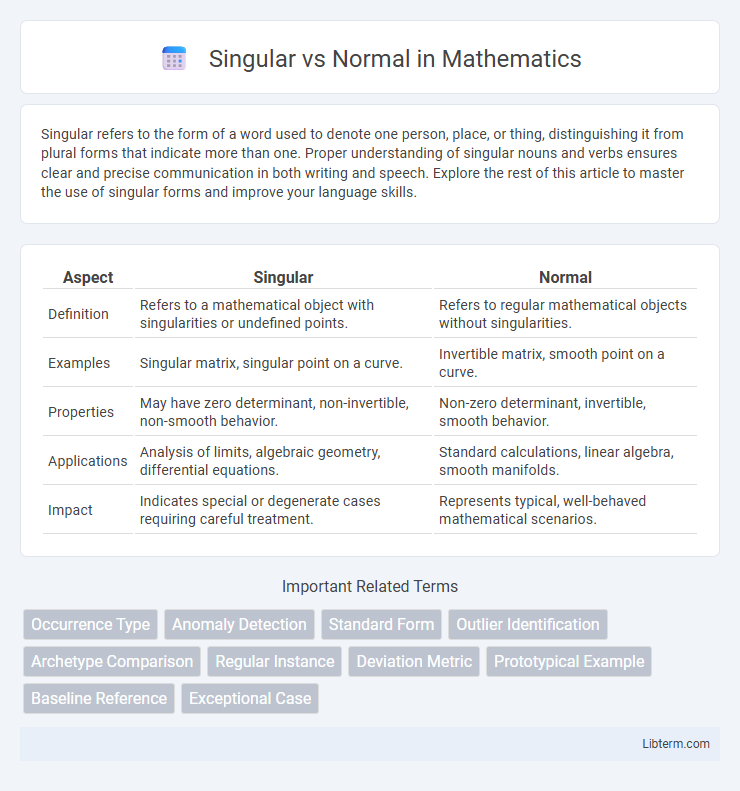
| Aspect | Singular | Normal |
|---|---|---|
| Definition | Refers to a mathematical object with singularities or undefined points. | Refers to regular mathematical objects without singularities. |
| Examples | Singular matrix, singular point on a curve. | Invertible matrix, smooth point on a curve. |
| Properties | May have zero determinant, non-invertible, non-smooth behavior. | Non-zero determinant, invertible, smooth behavior. |
| Applications | Analysis of limits, algebraic geometry, differential equations. | Standard calculations, linear algebra, smooth manifolds. |
| Impact | Indicates special or degenerate cases requiring careful treatment. | Represents typical, well-behaved mathematical scenarios. |
Understanding Singular and Normal: Key Definitions
Singular refers to a grammatical number used when discussing one item or entity, essential for correct subject-verb agreement in English language structure. Normal typically describes the plural form or standard, regular usage in contrast to singular, highlighting the typical or expected quantity or condition. Understanding these key definitions enhances clarity in communication and precision in language mechanics.
Core Differences Between Singular and Normal
Singular nouns refer to one single entity, whereas normal, or plural, nouns denote more than one. Singular forms typically do not end with an "s," unlike normal plural forms which usually add "s" or "es." Verb agreement changes accordingly: singular subjects pair with singular verbs, while plural subjects match plural verbs, highlighting a core grammatical difference.
Real-World Examples of Singular and Normal
Apple Inc. represents a singular example of innovation, pioneering products like the iPhone that revolutionized the smartphone industry, while normal companies often follow established market trends without radical shifts. In transportation, Tesla showcases singular advancements with its electric vehicles and autopilot technology, contrasting with traditional automakers producing normal combustion engine cars. Retail giants like Amazon demonstrate singular disruptive business models through e-commerce and logistics innovation, whereas typical brick-and-mortar stores maintain normal operational methods.
Applications of Singular vs Normal in Various Fields
Singular matrices play a critical role in control systems and signal processing, where they indicate non-invertible transformations that affect system stability and filter design. Normal matrices, characterized by their commutation with their conjugate transpose, are fundamental in quantum mechanics and machine learning for diagonalization and spectral analysis, enabling efficient computation and data dimensionality reduction. In computer graphics and physics simulations, normal matrices ensure orthogonality and preserve vector magnitudes, while singular matrices highlight degeneracies or constraints within modeled systems.
Semantic Implications: Singular vs Normal
Singular forms emphasize individual entities, enhancing precision in semantic interpretation by limiting context to a single item or concept, which reduces ambiguity in information retrieval and natural language processing tasks. Normal or plural forms convey generality or multiplicity, enabling broader categorization and pattern recognition in linguistic analysis while potentially introducing ambiguity due to the inclusion of multiple subjects or objects. Understanding the semantic implications of singular versus normal usage is crucial for optimizing search algorithms, knowledge representation, and automated reasoning systems that rely on accurate entity disambiguation.
Advantages of Using Singular Forms
Using singular forms in writing and data labeling improves clarity and precision, reducing ambiguity in communication. Singular terms enhance search engine optimization (SEO) by aligning better with specific queries, increasing content relevancy and user engagement. Consistent use of singular forms also simplifies data processing and categorization in databases and programming, improving efficiency and accuracy.
Benefits of Normal Usage
Normal usage promotes clarity and ease of understanding by aligning with common language patterns, facilitating effective communication. It reduces ambiguity and cognitive load, enabling users to quickly interpret and process information. Widespread adoption of normal usage supports consistency in documentation and software development, enhancing maintainability and collaboration.
Common Misconceptions About Singular and Normal
Common misconceptions about singular and normal matrices include the belief that all singular matrices are non-invertible, which is true, but not all non-invertible matrices are singular in certain extended algebraic systems. Another misunderstanding is that normal matrices must be diagonal, whereas normal matrices are defined by the commutation with their conjugate transpose, allowing for more general forms. These distinctions are critical in linear algebra for correctly classifying matrix behaviors and properties.
Choosing Between Singular and Normal: Best Practices
Choosing between Singular and Normal relies on understanding their unique benefits and applications; Singular excels in representing specific, distinct entities while Normal suits broader, more general categorizations. Best practices recommend using Singular forms for precise data modeling and search engine optimization, enhancing clarity and relevance in user queries. Normal forms are preferred when capturing recurring, collective concepts to maintain consistency and reduce redundancy in datasets.
Future Trends in the Use of Singular and Normal
Future trends indicate a growing preference for singular forms in AI technology and data analytics, as singular entities offer more precise targeting and customization. Normal forms continue to dominate in large-scale data processing due to their efficiency in standardization and normalization tasks. Advances in machine learning favor hybrid approaches that leverage both singular precision and normal scalability to optimize performance across diverse applications.
Singular Infographic
 libterm.com
libterm.com