The nerve of a category is a fundamental construction in category theory that encodes a category as a simplicial set, capturing objects and morphisms in a combinatorial framework. This concept enables the translation of categorical properties into topological or homotopical contexts, facilitating deeper analysis using tools from algebraic topology. Explore the rest of the article to understand how the nerve construction bridges these mathematical domains and benefits your study of categories.
Table of Comparison
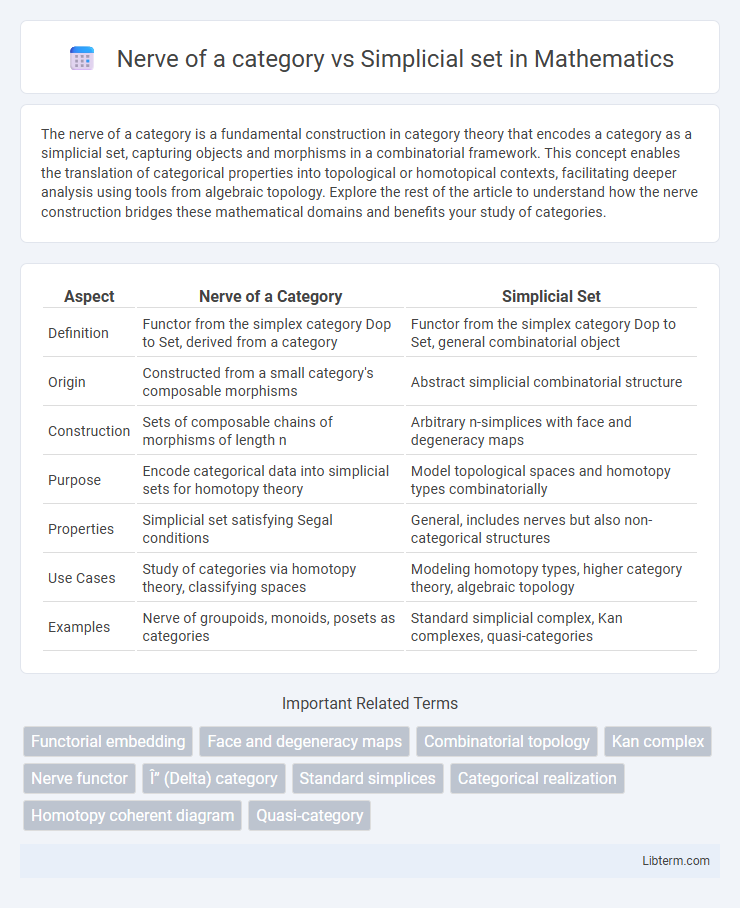
| Aspect | Nerve of a Category | Simplicial Set |
|---|---|---|
| Definition | Functor from the simplex category Dop to Set, derived from a category | Functor from the simplex category Dop to Set, general combinatorial object |
| Origin | Constructed from a small category's composable morphisms | Abstract simplicial combinatorial structure |
| Construction | Sets of composable chains of morphisms of length n | Arbitrary n-simplices with face and degeneracy maps |
| Purpose | Encode categorical data into simplicial sets for homotopy theory | Model topological spaces and homotopy types combinatorially |
| Properties | Simplicial set satisfying Segal conditions | General, includes nerves but also non-categorical structures |
| Use Cases | Study of categories via homotopy theory, classifying spaces | Modeling homotopy types, higher category theory, algebraic topology |
| Examples | Nerve of groupoids, monoids, posets as categories | Standard simplicial complex, Kan complexes, quasi-categories |
Introduction to Categories and Simplicial Sets
The nerve of a category is a simplicial set constructed by encoding objects as vertices and morphisms as higher-dimensional simplices, transforming categorical structures into combinatorial data. This correspondence enables the application of homotopical and topological methods to study categories through their nerves. Understanding this bridge is fundamental in the introduction to categories and simplicial sets, linking abstract algebraic concepts with geometric intuition.
Understanding the Nerve of a Category
The nerve of a category is a simplicial set constructed by encoding objects and morphisms into sequences of composable arrows, providing a combinatorial framework to study category theory through algebraic topology. Each n-simplex in the nerve corresponds to a string of n composable morphisms, translating categorical structures into simplicial complexes that facilitate homotopy-theoretic analysis. Understanding the nerve of a category bridges categorical concepts with simplicial homotopy theory, enabling invariants and equivalences in higher-dimensional algebra.
Basics of Simplicial Sets
The nerve of a category is a simplicial set constructed by associating each n-simplex with a sequence of n composable morphisms in the category, providing a bridge between category theory and simplicial topology. Simplicial sets consist of collections of sets indexed by non-negative integers with face and degeneracy maps satisfying simplicial identities, serving as combinatorial models for topological spaces. Understanding these basics clarifies how simplicial sets encode categorical structures and enable geometric realizations of categories as topological spaces.
Constructing the Nerve: From Categories to Simplicial Sets
Constructing the nerve of a category transforms categorical structures into simplicial sets by encoding objects as vertices and composable morphisms as higher-dimensional simplices. Each n-simplex corresponds to a sequence of n composable morphisms, capturing the compositional structure of the category within the simplicial framework. This construction enables the study of categories using topological and homotopical methods inherent to simplicial sets.
Properties of the Nerve Functor
The nerve functor assigns to each category a simplicial set that encodes compositional data through sequences of morphisms, preserving categorical structure in a homotopically meaningful way. It is fully faithful, embedding categories into simplicial sets, and it reflects equivalences of categories as weak homotopy equivalences of simplicial sets. The nerve functor also commutes with limits, ensuring the preservation of categorical limits when transferred to the simplicial set context.
Simplicial Sets as Categorical Models
Simplicial sets serve as powerful categorical models by encoding higher-dimensional category structures through combinatorial data, enabling the representation of complex homotopical and algebraic information. The nerve of a category is a fundamental example of a simplicial set, constructed by assigning to each n-simplex the set of composable chains of morphisms of length n, thereby capturing categorical composition and identity in a simplicial framework. This construction allows simplicial sets to generalize categories and model -categories, facilitating advanced studies in higher category theory and homotopy theory.
Comparing Nerves and General Simplicial Sets
The nerve of a category forms a simplicial set where each n-simplex corresponds to a composable sequence of n morphisms, embedding categorical structure into combinatorial data. General simplicial sets extend beyond nerves by allowing arbitrary collections of n-simplices without strict compositional constraints, enabling greater flexibility in modeling higher-dimensional topological and algebraic objects. Comparing nerves and general simplicial sets highlights that nerves capture strict categorical compositions while general simplicial sets provide a broader framework suitable for homotopy theory and abstract simplicial complexes.
Examples: Nerve Construction in Practice
The nerve of a category transforms a small category into a simplicial set by encoding objects as vertices and morphisms as edges, with composable sequences forming higher-dimensional simplices. For example, the nerve of the category with two objects and a single non-identity morphism corresponds to a simplicial set capturing a 1-simplex, illustrating how categorical composition translates into simplicial structure. This nerve construction facilitates the application of topological methods to categories by representing categorical data within the framework of simplicial sets, widely used in homotopy theory and higher category theory.
Applications in Homotopy Theory
The nerve of a category transforms categorical data into a simplicial set, enabling the application of homotopical methods in algebraic topology. This construction facilitates the study of classifying spaces and higher homotopy groups by encoding categorical structures as combinatorial objects suitable for homotopy-theoretic analysis. In homotopy theory, the nerve functor bridges category theory and simplicial homotopy, providing foundational tools for model categories and the study of -categories.
Summary: Key Differences and Connections
The nerve of a category is a simplicial set constructed by encoding objects and morphisms of a category into simplices, providing a combinatorial model of the category's structure. Simplicial sets serve as a more general framework for homotopy theory and higher-dimensional categories, where the nerve construction acts as a bridge translating categorical data into topological or simplicial contexts. Key differences lie in their origins and uses: nerves specifically capture categorical composition, while simplicial sets encompass a broader class of structures, yet both interconnect through the nerve functor linking category theory with homotopy and algebraic topology.
Nerve of a category Infographic
 libterm.com
libterm.com