A probability measure quantifies the likelihood of events within a defined sample space, assigning values between 0 and 1 that represent impossible to certain outcomes. This mathematical function follows axioms ensuring non-negativity, normalization, and countable additivity, crucial for modeling randomness in fields like statistics and finance. Explore the rest of this article to understand how probability measures form the foundation of probabilistic analysis and decision-making.
Table of Comparison
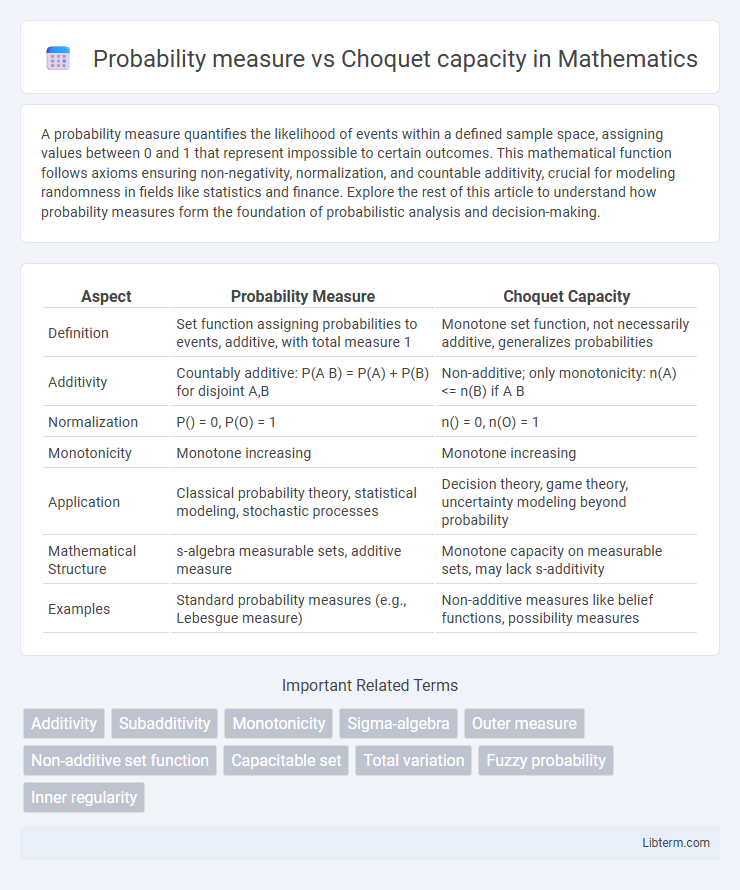
| Aspect | Probability Measure | Choquet Capacity |
|---|---|---|
| Definition | Set function assigning probabilities to events, additive, with total measure 1 | Monotone set function, not necessarily additive, generalizes probabilities |
| Additivity | Countably additive: P(A B) = P(A) + P(B) for disjoint A,B | Non-additive; only monotonicity: n(A) <= n(B) if A B |
| Normalization | P() = 0, P(O) = 1 | n() = 0, n(O) = 1 |
| Monotonicity | Monotone increasing | Monotone increasing |
| Application | Classical probability theory, statistical modeling, stochastic processes | Decision theory, game theory, uncertainty modeling beyond probability |
| Mathematical Structure | s-algebra measurable sets, additive measure | Monotone capacity on measurable sets, may lack s-additivity |
| Examples | Standard probability measures (e.g., Lebesgue measure) | Non-additive measures like belief functions, possibility measures |
Introduction to Probability Measures and Choquet Capacities
Probability measures assign a non-negative value to each event in a sigma-algebra, ensuring countable additivity and a total measure of one, which models uncertainty in classical probability theory. Choquet capacities generalize this concept by relaxing additivity to monotonicity, allowing for non-additive set functions that better capture ambiguity and uncertainty in decision-making contexts. This distinction highlights the foundational difference where probability measures quantify randomness precisely, while Choquet capacities accommodate more flexible representations of incomplete or imprecise information.
Mathematical Foundations of Probability Measures
Probability measures are countably additive set functions defined on sigma-algebras, assigning values between 0 and 1 to events, thereby satisfying Kolmogorov's axioms fundamental to classical probability theory. Choquet capacities generalize probability measures by relaxing countable additivity to monotonicity and continuity from below, enabling the modeling of uncertainty in non-additive frameworks such as imprecise probabilities and decision theory. The mathematical foundations of probability measures emphasize sigma-additivity and measurable spaces, whereas Choquet capacities arise in the study of monotone set functions and non-linear expectations, extending classical probability concepts to broader applications.
Defining Choquet Capacities: Key Concepts
Choquet capacities generalize probability measures by relaxing additivity to monotonicity, allowing for set functions that assign values based on the aggregation of uncertainties without requiring linearity. Unlike probability measures which satisfy countable additivity and normalize to one, Choquet capacities are defined on a measurable space as monotone, normalized, and continuous set functions that can model non-additive beliefs or capacities. Key concepts include monotonicity, normalization, and continuity properties such as continuity from below or above, which enable Choquet capacities to capture phenomena like ambiguity and uncertainty in decision theory.
Axiomatic Differences: Measures vs. Capacities
Probability measures follow countable additivity, requiring that the measure of a union of disjoint sets equals the sum of their measures, ensuring linearity and consistency over sigma-algebras. Choquet capacities relax this axiom to monotonicity and continuity conditions, allowing subadditivity or superadditivity instead of strict additivity, which accommodates uncertainty and ambiguity in set functions. This fundamental difference in axioms distinguishes probability measures as additive set functions, while Choquet capacities are non-additive, capturing a broader range of scenarios in decision theory and economics.
Additivity vs. Subadditivity: Core Properties Compared
Probability measures exhibit additivity, where the measure of a union of disjoint sets equals the sum of their individual measures, ensuring precise quantification of event likelihoods. Choquet capacities demonstrate subadditivity, assigning measures to unions of sets that are less than or equal to the sum of the measures of the individual sets, capturing ambiguity or non-additive uncertainty in decision theory. This fundamental distinction highlights probability measures' strict linearity versus Choquet capacities' flexibility in modeling non-linear aggregation of information.
Applications in Real-World Probability Modeling
Probability measures provide a precise mathematical framework for modeling uncertainty in real-world scenarios such as finance, insurance, and risk assessment, enabling exact calculation of event likelihoods based on additive properties. Choquet capacities extend beyond additive measures by accommodating non-additive beliefs and interactions, making them crucial in applications like decision theory, economics, and artificial intelligence where ambiguity and interconnected uncertainties prevail. Their flexibility allows for more accurate representations of real-world phenomena involving imprecise probabilities and subjective judgments, enhancing robustness in stochastic modeling and risk management.
Advantages of Using Choquet Capacities
Choquet capacities generalize probability measures by allowing non-additive set functions, which effectively model ambiguity and uncertainty in decision-making where classical probability fails. They accommodate interactions among events, capturing phenomena like complementarity or redundancy that standard measures overlook. This flexibility makes Choquet capacities advantageous in fields such as economics, risk assessment, and artificial intelligence, where uncertainty is often imprecise or dependent.
Limitations and Challenges of Each Approach
Probability measures impose additivity constraints, limiting their ability to model ambiguity and uncertainty in scenarios with incomplete information, while Choquet capacities relax additivity to accommodate such uncertainties but introduce computational complexity and challenges in interpretation. Probability measures struggle with representing non-linear expectations and interactions between events, whereas Choquet capacities face difficulties in establishing unique representations and ensuring consistency in dynamic settings. Both approaches encounter obstacles in scalability and practical implementation, especially when dealing with high-dimensional data or complex dependence structures.
Case Studies: When to Use Probability Measures or Choquet Capacities
Case studies reveal probability measures excel in modeling situations with additive uncertainty and well-defined probability distributions, such as in classic risk assessment and statistical inference. Choquet capacities prove more effective in scenarios involving ambiguous or non-additive uncertainty, notably in decision-making under ambiguity, game theory, and economics with imprecise probabilities. Understanding the nature of uncertainty and the requirement for additivity or non-additivity guides the appropriate choice between probability measures and Choquet capacities.
Conclusion: Choosing the Right Framework for Uncertainty
Probability measures provide precise numerical values adhering to additivity and normalization, ideal for modeling well-defined uncertain events. Choquet capacities offer a flexible, non-additive framework better suited for representing ambiguous or imprecise information, capturing phenomena like belief functions and fuzzy measures. Selecting the right framework depends on the nature of uncertainty involved: use probability measures for quantifiable risk, and Choquet capacities for scenarios involving ambiguity or incomplete knowledge.
Probability measure Infographic
 libterm.com
libterm.com