Mastering the specific field you are passionate about can significantly boost your expertise and career prospects. Focused knowledge and practical experience in your chosen field will help you stand out in a competitive job market. Explore the article further to discover strategies for advancing your skills and opportunities within your field.
Table of Comparison
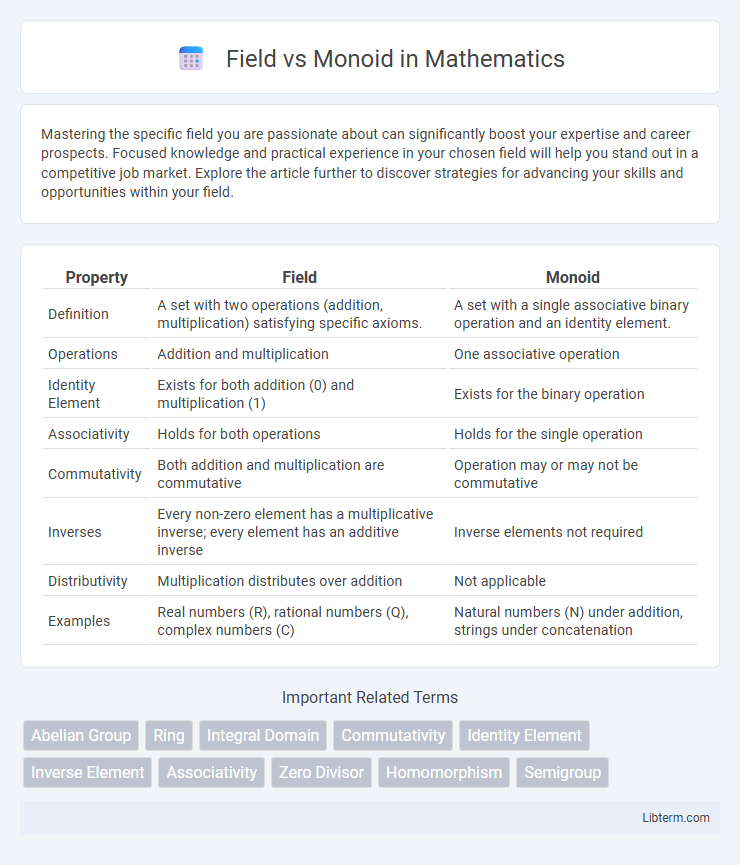
| Property | Field | Monoid |
|---|---|---|
| Definition | A set with two operations (addition, multiplication) satisfying specific axioms. | A set with a single associative binary operation and an identity element. |
| Operations | Addition and multiplication | One associative operation |
| Identity Element | Exists for both addition (0) and multiplication (1) | Exists for the binary operation |
| Associativity | Holds for both operations | Holds for the single operation |
| Commutativity | Both addition and multiplication are commutative | Operation may or may not be commutative |
| Inverses | Every non-zero element has a multiplicative inverse; every element has an additive inverse | Inverse elements not required |
| Distributivity | Multiplication distributes over addition | Not applicable |
| Examples | Real numbers (R), rational numbers (Q), complex numbers (C) | Natural numbers (N) under addition, strings under concatenation |
Introduction to Field and Monoid
A field is an algebraic structure consisting of a set equipped with two operations, addition and multiplication, where every non-zero element has a multiplicative inverse, enabling division. A monoid is a simpler algebraic structure with a single associative binary operation and an identity element, but it does not require invertibility or commutativity. Fields are foundational in linear algebra and abstract algebra, while monoids are essential in computer science and automata theory for modeling state transitions and concatenations.
Defining a Monoid: Basic Concepts
A monoid is an algebraic structure consisting of a set equipped with a single associative binary operation and an identity element, ensuring closure under the operation. Unlike a field, a monoid does not require invertibility of elements or the presence of a second operation such as addition and multiplication. The fundamental properties defining a monoid are associativity and the existence of an identity element that leaves other elements unchanged under the operation.
Key Properties of Monoids
Monoids are algebraic structures defined by a single associative binary operation and an identity element, unlike fields that require two operations with complex axioms including multiplicative inverses. Key properties of monoids include closure, associativity, and the existence of an identity element that leaves other elements unchanged under the operation. These fundamental characteristics enable monoids to serve as a simpler foundation in abstract algebra and computer science, especially in the study of strings, numbers, and functional programming.
Exploring Fields: Fundamental Definitions
Fields are algebraic structures consisting of a set equipped with two operations: addition and multiplication, where every non-zero element has a multiplicative inverse, making division possible. Unlike monoids, which require only a single associative operation with an identity element, fields demand both operations to form abelian groups under addition and multiplication. Fundamental definitions of fields emphasize closure, associativity, distributivity, identity elements, and the existence of inverses for all elements excluding zero under multiplication.
Essential Properties of Fields
Fields are algebraic structures equipped with two binary operations, addition and multiplication, satisfying essential properties such as commutativity, associativity, distributivity, the existence of additive and multiplicative identities, and inverses for all non-zero elements. Unlike monoids, which require associativity and an identity element for a single operation, fields demand that multiplication forms an abelian group excluding zero, ensuring every non-zero element has a multiplicative inverse. These properties enable fields to support division, distinguishing them fundamentally from monoids and enhancing their applicability in linear algebra and number theory.
Field vs Monoid: Structural Differences
A Field is an algebraic structure equipped with two operations, addition and multiplication, both of which are associative, commutative, and have identity elements, with every nonzero element having a multiplicative inverse. A Monoid consists of a single associative binary operation with an identity element, but it does not require commutativity, inverses, or multiple operations. The fundamental structural difference lies in a Field's dual operation system with strict inverse and commutativity requirements versus a Monoid's single operation with minimal constraints.
Examples of Monoids and Fields
A field, such as the set of real numbers \(\mathbb{R}\) under addition and multiplication, supports division by any non-zero element, making it a richer algebraic structure than a monoid. Monoids include simpler examples like the set of natural numbers \(\mathbb{N}\) under addition, with the identity element zero, or strings under concatenation with the empty string as the identity. Unlike fields, monoids require only an associative binary operation and an identity element, without the need for inverses or multiple operations.
Applications of Monoids in Mathematics
Monoids play a crucial role in various mathematical fields by providing a simplified algebraic structure that supports associative binary operations and an identity element, essential in category theory and automata theory. Their applications extend to computer science, where monoids underpin the design of efficient algorithms for string processing, parallel computing, and formal language theory. Unlike fields, which require both additive and multiplicative inverses, monoids offer a more flexible framework applicable to optimization problems and abstract algebraic systems without necessitating full invertibility.
Fields in Algebra: Role and Importance
Fields in algebra play a crucial role as they provide a fundamental structure where addition, subtraction, multiplication, and division (except by zero) are all well-defined and satisfy specific axioms. Unlike monoids, which only require an associative binary operation and an identity element, fields enable the existence of multiplicative inverses, allowing for division and the formulation of linear algebra, polynomial theory, and number systems such as the rational, real, and complex numbers. The importance of fields lies in their comprehensive algebraic framework that supports advanced mathematical concepts, including vector spaces and algebraic extensions, making them indispensable in both theoretical and applied mathematics.
Summary: Monoid vs Field Comparison
A monoid is an algebraic structure with a single associative binary operation and an identity element, supporting closure but not requiring inverses for every element. A field is a more complex structure with two operations (addition and multiplication), where every nonzero element has a multiplicative inverse, satisfying properties of commutativity, associativity, distributivity, and identity for both operations. The key distinction lies in fields having multiplicative inverses and two operations, enabling division, while monoids have only one associative operation and do not guarantee inverses.
Field Infographic
 libterm.com
libterm.com