Energy function plays a crucial role in physics and machine learning by quantifying the state of a system through a scalar value that measures potential or cost. It helps in optimizing models and understanding dynamic behaviors by guiding systems toward equilibrium or minimal energy states. Explore the rest of the article to discover how energy functions impact various fields and enhance your problem-solving techniques.
Table of Comparison
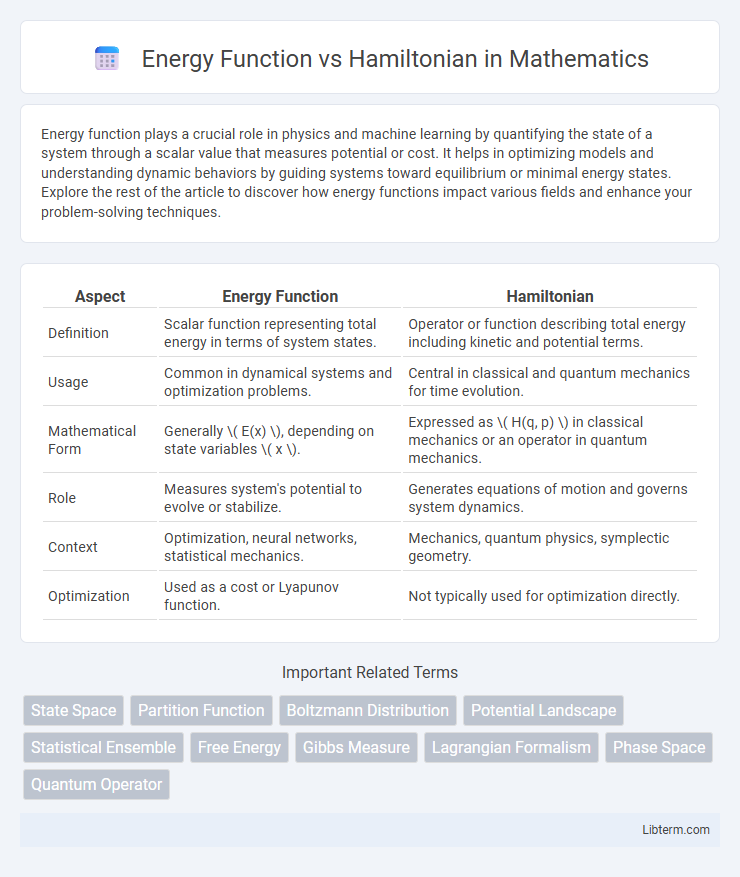
| Aspect | Energy Function | Hamiltonian |
|---|---|---|
| Definition | Scalar function representing total energy in terms of system states. | Operator or function describing total energy including kinetic and potential terms. |
| Usage | Common in dynamical systems and optimization problems. | Central in classical and quantum mechanics for time evolution. |
| Mathematical Form | Generally \( E(x) \), depending on state variables \( x \). | Expressed as \( H(q, p) \) in classical mechanics or an operator in quantum mechanics. |
| Role | Measures system's potential to evolve or stabilize. | Generates equations of motion and governs system dynamics. |
| Context | Optimization, neural networks, statistical mechanics. | Mechanics, quantum physics, symplectic geometry. |
| Optimization | Used as a cost or Lyapunov function. | Not typically used for optimization directly. |
Understanding the Basics: Energy Function and Hamiltonian
The Energy function represents the total energy of a system, often used in physics and machine learning to describe potential and kinetic components within a state. The Hamiltonian is a specific type of energy function that formalizes the total energy in classical mechanics, combining kinetic and potential energies into a single scalar function governing system dynamics. Understanding the Hamiltonian's role in evolution equations and symplectic geometry is crucial for advanced analysis in physics and related fields.
Fundamental Definitions and Mathematical Formulation
The energy function in physics represents a scalar quantity describing the total energy of a system, often expressed as \(E = T + V\), where \(T\) is kinetic energy and \(V\) is potential energy. The Hamiltonian, denoted \(H(q, p)\), is a specific energy function reformulated in terms of generalized coordinates \(q\) and conjugate momenta \(p\), serving as the generator of time evolution in Hamiltonian mechanics with the mathematical form \(H = \sum_i p_i \dot{q}_i - L\), where \(L\) is the Lagrangian. While both quantify system energy, the Hamiltonian's structure allows the use of canonical equations \(\dot{q}_i = \frac{\partial H}{\partial p_i}\) and \(\dot{p}_i = -\frac{\partial H}{\partial q_i}\), central to advanced dynamical analyses.
Historical Context and Development
The energy function concept originated in classical mechanics, describing the total energy of a system as the sum of kinetic and potential energies, whereas the Hamiltonian formalism, developed by William Rowan Hamilton in the 19th century, reformulated mechanics through a function representing the total energy but expressed in terms of coordinates and conjugate momenta. This Hamiltonian approach paved the way for the transition from classical to quantum mechanics, influencing the development of Schrodinger's equation and modern theoretical physics. The historical progression from energy functions to Hamiltonians reflects a significant shift towards more abstract and generalized mathematical frameworks in physics.
Role in Classical Mechanics
The energy function in classical mechanics typically refers to the total energy of a system expressed as a function of generalized coordinates and momenta, often represented by the Hamiltonian. The Hamiltonian serves as the central entity dictating the time evolution of a system through Hamilton's equations, encapsulating both kinetic and potential energy. Its role extends to generating canonical transformations and providing a framework for transitioning from classical to quantum mechanics.
Application in Quantum Mechanics
In quantum mechanics, the Hamiltonian operator represents the total energy of a system, including kinetic and potential energies, and governs the time evolution via the Schrodinger equation. The energy function, often seen as the classical counterpart, describes the system's energy landscape but lacks operator properties essential for quantum state analysis. Understanding the Hamiltonian's role enables precise computation of energy eigenvalues and eigenstates, crucial for predicting quantum behaviors and observables.
Key Differences Between Energy Function and Hamiltonian
Energy functions represent scalar quantities describing the total energy of a system, often used in optimization and machine learning contexts to evaluate system states. Hamiltonians, fundamental in classical and quantum mechanics, combine kinetic and potential energy into a single operator that governs system dynamics through Hamilton's equations. Unlike general energy functions, Hamiltonians explicitly encode time evolution and symplectic structure, enabling precise prediction of system trajectories.
Similarities and Overlapping Concepts
Energy functions and Hamiltonians both represent scalar quantities describing the total energy of physical systems in classical and quantum mechanics. They encompass kinetic and potential energy components, serving as fundamental tools for analyzing system dynamics and stability through equations of motion. Both functionals enable the application of variational principles and facilitate the study of conserved quantities in physics.
Practical Examples in Physics and Engineering
Energy functions and Hamiltonians both describe total energy in physical systems, but the Hamiltonian is often used in quantum mechanics and classical mechanics to generate equations of motion through Hamilton's equations. For example, in engineering, the energy function is used in structural analysis to calculate potential and kinetic energy for stability assessments, while the Hamiltonian framework is critical in designing control systems and simulating particle dynamics. Practical applications include electrical circuit design, where energy functions determine stored energy, and molecular dynamics simulations, where Hamiltonians govern the behavior of interacting particles.
Implications for Modern Research and Technology
Energy functions and Hamiltonians play pivotal roles in modern research and technology by providing foundational frameworks for understanding physical systems and optimizing computational models. The Hamiltonian formalism, central to quantum mechanics and statistical physics, enables precise descriptions of system dynamics, facilitating advancements in quantum computing and material sciences. Energy functions, often employed in machine learning and optimization algorithms, enhance pattern recognition and decision-making processes, driving innovation in artificial intelligence and complex network analysis.
Summary and Future Perspectives
Energy functions quantify system states by assigning scalar values representing system stability or cost, widely used in optimization and machine learning. Hamiltonians extend energy functions by incorporating both kinetic and potential energy, serving as foundational tools in classical mechanics and quantum physics for describing system evolution. Future research aims to unify these concepts further, enhancing computational methods in physics-informed machine learning and enabling more accurate modeling of complex dynamical systems.
Energy Function Infographic
 libterm.com
libterm.com